 παίρνω σημείο Δ, τέτοιο ώστε
παίρνω σημείο Δ, τέτοιο ώστε  και
και  . Βρείτε τη γωνία x.
. Βρείτε τη γωνία x.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
 παίρνω σημείο Δ, τέτοιο ώστε
παίρνω σημείο Δ, τέτοιο ώστε  και
και  . Βρείτε τη γωνία x.
. Βρείτε τη γωνία x.



 , καθώς ο νόμως των συνημιτόνων στο ΔΒΓ δίνει:
, καθώς ο νόμως των συνημιτόνων στο ΔΒΓ δίνει:
 είναι της μορφής
είναι της μορφής  .
.
 είναι ρίζες της εξίσωσης.
είναι ρίζες της εξίσωσης.

 θα είναιι τότε:
θα είναιι τότε:

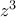 :
:
 ακολουθώντας όμοια πάλι την ίδια διαδικασία θα λάβουμε:
ακολουθώντας όμοια πάλι την ίδια διαδικασία θα λάβουμε: . Άρα οι αριθμοί
. Άρα οι αριθμοί 
 .
.
 αφού είναι ισοσκελές και πρέπει αναγκαστικα να είναι οξεία.
αφού είναι ισοσκελές και πρέπει αναγκαστικα να είναι οξεία. τότε θα είναι η γωνία Α
τότε θα είναι η γωνία Α  άτοπο αφού
άτοπο αφού  .Άρα θα είναι:
.Άρα θα είναι:
 .
.  οπότε:
οπότε: 




 μάς οδηγεί στην τιμή
μάς οδηγεί στην τιμή  .
. και χρησιμοποιώντας τους τύπους:
και χρησιμοποιώντας τους τύπους:  είναι
είναι 
 ,
, 

![\displaystyle
\begin{array}{l}
= 2\sigma \upsilon \nu \frac{{3\pi }}{7} + 2\sigma \upsilon \nu \frac{{5\pi }}{7} + 2\sigma \upsilon \nu \frac{\pi }{7} - 1 = \\
\\
= \frac{1}{{\eta \mu \frac{\pi }{7}}}\left[ {2\eta \mu \frac{\pi }{7}\sigma \upsilon \nu \frac{{3\pi }}{7} + 2\eta \mu \frac{\pi }{7}\sigma \upsilon \nu \frac{{5\pi }}{7} + 2\eta \mu \frac{\pi }{7}\sigma \upsilon \nu \frac{\pi }{7}} \right] - 1 = \\
\end{array} \displaystyle
\begin{array}{l}
= 2\sigma \upsilon \nu \frac{{3\pi }}{7} + 2\sigma \upsilon \nu \frac{{5\pi }}{7} + 2\sigma \upsilon \nu \frac{\pi }{7} - 1 = \\
\\
= \frac{1}{{\eta \mu \frac{\pi }{7}}}\left[ {2\eta \mu \frac{\pi }{7}\sigma \upsilon \nu \frac{{3\pi }}{7} + 2\eta \mu \frac{\pi }{7}\sigma \upsilon \nu \frac{{5\pi }}{7} + 2\eta \mu \frac{\pi }{7}\sigma \upsilon \nu \frac{\pi }{7}} \right] - 1 = \\
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/15774987f15ab28a2ec1c4fda67139e5.png)
![\displaystyle
= \frac{1}{{\eta \mu \frac{\pi }{7}}}\left[ {\eta \mu \frac{{4\pi }}{7} - \eta \mu \frac{{2\pi }}{7} + \eta \mu \frac{{6\pi }}{7} - \eta \mu \frac{{4\pi }}{7} + \eta \mu \frac{{2\pi }}{7}} \right] - 1 = \frac{{\eta \mu \frac{{6\pi }}{7}}}{{\eta \mu \frac{\pi }{7}}} - 1 = 0 \displaystyle
= \frac{1}{{\eta \mu \frac{\pi }{7}}}\left[ {\eta \mu \frac{{4\pi }}{7} - \eta \mu \frac{{2\pi }}{7} + \eta \mu \frac{{6\pi }}{7} - \eta \mu \frac{{4\pi }}{7} + \eta \mu \frac{{2\pi }}{7}} \right] - 1 = \frac{{\eta \mu \frac{{6\pi }}{7}}}{{\eta \mu \frac{\pi }{7}}} - 1 = 0](/forum/ext/geomar/texintegr/latexrender/pictures/63f3f34dd771cba211cb19a02d7c36b0.png) ,
, επαληθεύει την εξίσωση.
επαληθεύει την εξίσωση.![\displaystyle
\left[ {\frac{{\sqrt 2 }}{2},\;1} \right] \displaystyle
\left[ {\frac{{\sqrt 2 }}{2},\;1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/876b5d02375c913a9ea787254d762012.png) , οπότε η λύση
, οπότε η λύση  είναι μόνη δεκτή.
είναι μόνη δεκτή. . Θέτω
. Θέτω  και
και  . Τα τρίγωνα ΔΒΓ και ΕΒΓ είναι ίσα από Π-Γ-Π, οπότε
. Τα τρίγωνα ΔΒΓ και ΕΒΓ είναι ίσα από Π-Γ-Π, οπότε  .
. , επομένως το τετράπλευρο ΔΕΓΒ είναι εγγράψιμο (μια γωνία είναι ίση με την απέναντι εξωτερική του γωνία).
, επομένως το τετράπλευρο ΔΕΓΒ είναι εγγράψιμο (μια γωνία είναι ίση με την απέναντι εξωτερική του γωνία). .
. και θα ισχύει
και θα ισχύει  (λόγω του ισοσκελούς ΕΖΑ) και
(λόγω του ισοσκελούς ΕΖΑ) και  .
. είναι εξωτερική γωνία του τριγώνου ΔΖΑ θα ισχύει
είναι εξωτερική γωνία του τριγώνου ΔΖΑ θα ισχύει  .
. . Από Π-Γ-Π τα τρίγωνα ΚΑΕ και ΑΒΓ είναι ίσα, επομένως
. Από Π-Γ-Π τα τρίγωνα ΚΑΕ και ΑΒΓ είναι ίσα, επομένως  και
και  . (**)
. (**) και από τη σχέση (1) προκύπτει ότι το τρίγωνο ΖΚΑ είναι ισοσκελές, οπότε
και από τη σχέση (1) προκύπτει ότι το τρίγωνο ΖΚΑ είναι ισοσκελές, οπότε  .
. .
.
 από τη σχέση (1) και από το θεώρημα διχοτόμων στο τρίγωνο ΑΚΔ. Κατέληξα στην τριτοβάθμια εξίσωση
από τη σχέση (1) και από το θεώρημα διχοτόμων στο τρίγωνο ΑΚΔ. Κατέληξα στην τριτοβάθμια εξίσωση  , η οποία έχει μια θετική ρίζα, αλλά το πράγμα γινόταν περίπλοκο…
, η οποία έχει μια θετική ρίζα, αλλά το πράγμα γινόταν περίπλοκο…Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες