gbaloglou έγραψε:Ερώτηση που λαθρότυχα προέκυψε από το παραπάνω σχήμα (και θα μπορούσε να τεθεί ανεξάρτητα): θα μπορούσε ποτέ η μωβ γραμμή να περάσει ποτέ από την κάτω δεξιά γωνία του πακέτου; (Καλύτερα όχι, γιατί τότε ... θα μπορούσε ίσως να περάσει και μέσα από την κορυφή, οπότε θα είχαμε πρόβλημα με την λύση που μόλις παρουσίασα

)
Μια και κανένας δεν ασχολήθηκε με το παραπάνω ερώτημα και την απαιτούμενη απάντηση:
Διαπιστώνω ότι η μωβ γραμμή διέρχεται πάντοτε από την κάτω δεξιά γωνία του μαύρου ορθογωνίου, άρα δεν μπορεί ποτέ να περάσει μέσα από αυτήν!
Αυτό μπορεί να το επαληθεύσει κανείς με δύο κόλλες χαρτί, αλλά για αυστηρή απόδειξη ... παραπέμπω στο συνημμένο ατελές σχήμα ... όπου υποθέτω ότι η μωβ γραμμή περνάει από την κάτω δεξιά κορυφή ... και αποδεικνύω ότι

(μέσω των

και

):
-- Για την

παρατηρούμε, χρησιμοποιώντας στο τέλος τον τύπο

(από προηγούμενη ανάρτηση μου), ότι
![y^2=(b-\sqrt{b^2-a^2})^2+x^2=b^2-2b\sqrt{b^2-a^2}+(b^2-a^2)+x^2=a^2-2[b\sqrt{b^2-a^2}-(b^2-a^2)]+x^2=a^2-2ax+x^2=(a-x)^2 y^2=(b-\sqrt{b^2-a^2})^2+x^2=b^2-2b\sqrt{b^2-a^2}+(b^2-a^2)+x^2=a^2-2[b\sqrt{b^2-a^2}-(b^2-a^2)]+x^2=a^2-2ax+x^2=(a-x)^2](/forum/ext/geomar/texintegr/latexrender/pictures/1d5f39d4e3071868ca19838aec92ab4b.png)
-- Για την

βασιζόμαστε στην μόλις αποδειχθείσα

και στην ομοιότητα των μικρών ορθογωνίων τριγώνων:

[Άκρως ενδιαφέρον πρόβλημα -- δύσκολο 'υπολογιστικά' (εκτός και αν μου διαφεύγει κάτι πιο έξυπνο*) και όμως τόσο εύκολο που "τυλίγεται σε δυο κόλλες χαρτί": στην γυμνασιακή τάξη θα μπορούσε ο καθηγητής να ζητήσει από τα παιδιά να το επαληθεύσουν 'πειραματικά' (είτε με τις δύο κόλλες χαρτί είτε με συγκεκριμένα παραδείγματα όπως

).]
*καλώ τους γεωμέτρες του

να επέμβουν άμεσα -- έχει προκύψει 'χαρταετός' (
kite), άρα ... κάτι θα κρύβεται πίσω από τα αλευρόκουτα

Γιώργος Μπαλόγλου
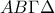 πλευράς
πλευράς  , αναδιπλώνεται κατά μήκος ευθυγράμμου τμήματος
, αναδιπλώνεται κατά μήκος ευθυγράμμου τμήματος  , ώστε η κορυφή
, ώστε η κορυφή  να ταυτιστεί με το μέσο της πλευράς
να ταυτιστεί με το μέσο της πλευράς  . Αν οι νέες θέσεις των
. Αν οι νέες θέσεις των  και
και  είναι οι
είναι οι  και
και  αντίστοιχα και
αντίστοιχα και  η τομή των
η τομή των  και
και  , τότε :
, τότε :  και
και  είναι όμοια.
είναι όμοια. .
.
 είναι ορθή (ως ίση προς την
είναι ορθή (ως ίση προς την  ) ... και τα ορθογώνια τρίγωνα
) ... και τα ορθογώνια τρίγωνα  και
και  είναι όντως όμοια (γωνίες με κάθετες πλευρές).
είναι όντως όμοια (γωνίες με κάθετες πλευρές). , και από το ορθογώνιο τρίγωνο
, και από το ορθογώνιο τρίγωνο  , οπότε εύκολα
, οπότε εύκολα  . Από την ομοιότητα των τριγώνων προκύπτει η
. Από την ομοιότητα των τριγώνων προκύπτει η  και η
και η  , άρα
, άρα  .
. , άρα και η
, άρα και η  .
.![\displaystyle\frac{a\sqrt{b^2-a^2}}{2}+\displaystyle\frac{(b-\sqrt{b^2-a^2})[b\sqrt{b^2-a^2}-(b^2-a^2)]}{2a} \displaystyle\frac{a\sqrt{b^2-a^2}}{2}+\displaystyle\frac{(b-\sqrt{b^2-a^2})[b\sqrt{b^2-a^2}-(b^2-a^2)]}{2a}](/forum/ext/geomar/texintegr/latexrender/pictures/5d4ad2796fb5829c23e84f784662f018.png) , είναι επομένως μικρότερο του εμβαδού του κρυμμένου τμήματος αν και μόνον είναι μικρότερο του μισού εμβαδού του πακέτου, δηλαδή αν και μόνον αν ισχύει η σχέση
, είναι επομένως μικρότερο του εμβαδού του κρυμμένου τμήματος αν και μόνον είναι μικρότερο του μισού εμβαδού του πακέτου, δηλαδή αν και μόνον αν ισχύει η σχέση ![\displaystyle\frac{a\sqrt{b^2-a^2}}{2}+\displaystyle\frac{(b-\sqrt{b^2-a^2})[b\sqrt{b^2-a^2}-(b^2-a^2)]}{2a}<\displaystyle\frac{ab}{2}\Leftrightarrow 2b\sqrt{b^2-a^2}<2b^2-a^2\Leftrightarrow 0<a^4 \displaystyle\frac{a\sqrt{b^2-a^2}}{2}+\displaystyle\frac{(b-\sqrt{b^2-a^2})[b\sqrt{b^2-a^2}-(b^2-a^2)]}{2a}<\displaystyle\frac{ab}{2}\Leftrightarrow 2b\sqrt{b^2-a^2}<2b^2-a^2\Leftrightarrow 0<a^4](/forum/ext/geomar/texintegr/latexrender/pictures/86bca9133c03678ef28013a02bc74994.png)
 (μέσω των
(μέσω των  και
και  ):
):![y^2=(b-\sqrt{b^2-a^2})^2+x^2=b^2-2b\sqrt{b^2-a^2}+(b^2-a^2)+x^2=a^2-2[b\sqrt{b^2-a^2}-(b^2-a^2)]+x^2=a^2-2ax+x^2=(a-x)^2 y^2=(b-\sqrt{b^2-a^2})^2+x^2=b^2-2b\sqrt{b^2-a^2}+(b^2-a^2)+x^2=a^2-2[b\sqrt{b^2-a^2}-(b^2-a^2)]+x^2=a^2-2ax+x^2=(a-x)^2](/forum/ext/geomar/texintegr/latexrender/pictures/1d5f39d4e3071868ca19838aec92ab4b.png)

 ).]
).] (
( , από ίσα ορθογώνια τρίγωνα
, από ίσα ορθογώνια τρίγωνα  ), οπότε προκύπτει και η ζητούμενη
), οπότε προκύπτει και η ζητούμενη  όπως πριν (και ίσα ορθογώνια τρίγωνα
όπως πριν (και ίσα ορθογώνια τρίγωνα  ), κλπ
), κλπ και
και  τα σημεία τομής των ομόλογων πλευρών. Τότε,
τα σημεία τομής των ομόλογων πλευρών. Τότε,  και αν
και αν , το
, το  είναι κέντρο στροφής που απεικονίζει το
είναι κέντρο στροφής που απεικονίζει το  στο
στο  . Δηλαδή
. Δηλαδή  και
και  . Υπάρχει άλλο ένα κέντρο, αν αλλάξουμε την αντιστοιχία των κορυφών. Αν έχουμε διαφορετικό προσανατολισμό, πρέπει να κάνουμε επι πλέον και μία ανάκλαση.
. Υπάρχει άλλο ένα κέντρο, αν αλλάξουμε την αντιστοιχία των κορυφών. Αν έχουμε διαφορετικό προσανατολισμό, πρέπει να κάνουμε επι πλέον και μία ανάκλαση. ,
,  στρέφονται περί το
στρέφονται περί το  , και
, και  , τότε
, τότε  .
. είναι συνευθειακά.
είναι συνευθειακά. , άρα
, άρα  .]
.] κλπ
κλπ  Έστω
Έστω  οι προβολές του σημείου
οι προβολές του σημείου  επί των
επί των  αντιστοίχως και έχουμε ότι ο κύκλος έστω
αντιστοίχως και έχουμε ότι ο κύκλος έστω  με κέντρο το
με κέντρο το  εφάπτεται των
εφάπτεται των  όπου
όπου  και
και 
 και έχουμε ότι το παραλληλόγραμμο
και έχουμε ότι το παραλληλόγραμμο  , όπου
, όπου  και
και  είναι ρόμβος λόγω
είναι ρόμβος λόγω  όπου
όπου  είναι οι προβολές του
είναι οι προβολές του  επί των
επί των  αντιστοίχως ( παραλληλόγραμμο με ίσα ύψη είναι ρόμβος ).
αντιστοίχως ( παραλληλόγραμμο με ίσα ύψη είναι ρόμβος ). διχοτομεί την γωνία
διχοτομεί την γωνία  και από
και από  και
και  προκύπτει ότι
προκύπτει ότι  και άρα λόγω της
και άρα λόγω της  έχουμε ότι
έχουμε ότι 
 και
και  , λόγω του ρόμβου
, λόγω του ρόμβου  συμπεραίνεται ότι
συμπεραίνεται ότι  προκύπτουν άμεσα οι απαιτούμενες ισότητες γωνιών
προκύπτουν άμεσα οι απαιτούμενες ισότητες γωνιών  , ενώ οι απαιτούμενες ισότητες μηκών όπως πχ η
, ενώ οι απαιτούμενες ισότητες μηκών όπως πχ η  προκύπτουν από θεωρήσεις τόξων (στον περιγεγραμμένο κύκλο του
προκύπτουν από θεωρήσεις τόξων (στον περιγεγραμμένο κύκλο του  για παράδειγμα, όπου χρειαζόμαστε και πάλι την μέθοδο του Κώστα για την
για παράδειγμα, όπου χρειαζόμαστε και πάλι την μέθοδο του Κώστα για την  (που μας δίνει την απαιτούμενη
(που μας δίνει την απαιτούμενη  λόγω της
λόγω της  )).
)). και
και  .
.