Άσκηση 24
Δύο ποδηλάτες ο Μίλτος και ο Στάθης έχουν να διανύσουν από 5 διαδρομές ο καθένας. Ο Μίλτος τις διαδρομές

και ο Στάθης τις διαδρομές

όπου

. Αν "προσομοιώσουμε" τις διαδρομές

αντίστοιχα με τις γραφικές παραστάσεις των συναρτήσεων

και

όπου

, να απαντήσετε στα εξής:
α) Για ποιές τιμές του λ οι διαδρομές

είναι ανηφορικές;
β) Για ποια τιμή του λ δε θα συναντηθούν ποτέ ο Μίλτος και ο Στάθης;
γ) Για ποιά τιμή του λ ο Μίλτος θα κουραστεί περισσότερο από το Στάθη;
δ) Αν οι δυο μας φίλοι θέλουν να ξεδιψάσουν στην μοναδική πηγή που βρίσκεται στο σημείο

ποια διαδρομή πρέπει να ακολουθήσει ο καθένας;
ε) Αν ο Μίλτος ακολουθήσει τη διαδρομή

και ο Στάθης τη διαδρομή

ποιο θα είναι το σημείο συνάντησης τους;
Παρατηρήσεις: οι αποστάσεις (x) εκφράζονται σε χιλιόμετρα και το (-) δηλώνει αντίθετη κατεύθυνση.
α. Επειδή οι γραφικές παραστάσεις των συναρτήσεων f(x) ,g(x) είναι ευθείες, θα είναι ανηφορικές εάν είναι γνησίως αύξουσες σαν συναρτήσεις, εαν δηλαδή έχουν θετικό συντελεστή διεύθυνσης οπότε:
Ο μεν Μίλτος ανηφορίζει όταν

κι επειδή

άρα όταν

.
Ο δε Στάθης ανηφορίζει όταν

κι επειδή

άρα όταν

.
β. Ο Μίλτος κι ο Στάθης που κινούνται πάνω σε ευθείες δεν θα συναντηθούν εφόσον οι ευθείες που κινούνται είναι παράλληλες, όταν δηλαδή έχουν τον ίδιο συντελεστή διεύθυνσης, οπότε :

δεκτή λύση.
Δηλαδή όσο κινείται ο Μίλτος στη

και ο Στάθης στην

, οι τροχιές των κινήσεων τους ποτέ δεν συναντιούνται.
γ.Ο Μίλτος θα κουραστεί περισσότερο από τον Στάθη όταν για την ίδια απόσταση διανύει πιο ανηφορικές διαδρομές, δηλαδή διαδρομές με μεγαλύτερη κλίση οπότε όταν


κι επειδή

τότε

.
Άρα σε καθεμία από τα διαδρομές

κουράζεται περισσότερο ο Μίλτος σε σχέση με τον Στάθη στις διαδρομές

αντίστοιχα,
δ.Για να ξεδιψάσουν στην πηγή στο σημείο

θα πρέπει οι συντεταγμένες της πηγής να επαληθεύουν τις γραφικές παραστάσεις των διαδρομών των ποδηλατών.
Ο Μίλτος :


ή
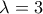
κι επειδή

τότε
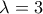
.
Ο Στάθης:


ή

κι επειδή

τότε
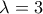
.
ε. Αν ο Μίλτος ακολουθήσει την διαδρομή

τότε θα κινείται στην ευθεία

.
Αν ο Στάθης ακολουθήσει την διαδρομή

τότε θα κινείται στην ευθεία

.
Οι δύο ποδηλάτες συναντιούνται όταν οι διαδρομές τους συναντιούνται, όταν


δεκτή λύση.

Το σημείο συνάντησης τους είναι το σημείο

.
edit1:
Διορθώθηκε η λανθασμένη λύση στο (γ) ερώτημα μετά την υπόδειξη του απόλυτα συνεργάσιμου και υπομονετικού pana1333
edit2: Μετέφερα τα ενδιάμεσα σχόλια στα υστερόγραφα
ΥΓ.1.Με βάση την απάντηση στο ερωτημα (α):
Πρώτη αδικία για τον Μίλτο: 4/5 οι ανηφόρες γι΄ αυτόν ενώ 3/5 οι ανηφόρες για τον Στάθη.
ΥΓ.2.Με βάση την απάντηση στο ερωτημα (γ):
Δεύτερη αδικία για τον Μίλτο: 3/5 οι διαδρομές που κουράζεται περισσότερο από τον Στάθη.
ΥΓ.3.Με βάση την απάντηση στο ερωτημα (δ):
Παραδόξως πάνε και οι δυο ποδηλάτες στην πηγη, το μόνο σημείο δικαιοσύνης στην άσκηση.
ΥΓ.4.Με βάση τα υστερόγραφα (1) και (2):
Ο θείος Χρήστος κάνει διακρίσεις καθώς ευνοεί επανειλημμένα τον Στάθη.Άρα η ζωή είναι άδικη

 εχουμε
εχουμε  . Άρα η (1) έχει τουλάχιστον μια λύση.
. Άρα η (1) έχει τουλάχιστον μια λύση. όπου τότε Δ>0 και για
όπου τότε Δ>0 και για 
 και
και 
 είναι
είναι 

 που ισχύει και κάθε πραγματικό m.
που ισχύει και κάθε πραγματικό m.

 είναι
είναι 

 έχουμε την ακέραια λύση
έχουμε την ακέραια λύση 

 :
:  και
και  :
:  όπου ο
όπου ο  είναι πραγματικός αριθμός.
είναι πραγματικός αριθμός. και
και 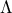 στα οποία οι
στα οποία οι  και
και  αντίστοιχα
αντίστοιχα  να ισχύει ότι
να ισχύει ότι 

 της ευθείας
της ευθείας  είναι σκαληνό.
είναι σκαληνό. που διέρχεται από τα
που διέρχεται από τα  που να είναι συμμετρικό κάποιου σημείου της
που να είναι συμμετρικό κάποιου σημείου της  ως προς άξονα συμμετρίας τον
ως προς άξονα συμμετρίας τον  και ο Στάθης τις διαδρομές
και ο Στάθης τις διαδρομές  όπου
όπου  . Αν "προσομοιώσουμε" τις διαδρομές
. Αν "προσομοιώσουμε" τις διαδρομές  αντίστοιχα με τις γραφικές παραστάσεις των συναρτήσεων
αντίστοιχα με τις γραφικές παραστάσεις των συναρτήσεων  και
και  όπου
όπου  , να απαντήσετε στα εξής:
, να απαντήσετε στα εξής: είναι ανηφορικές;
είναι ανηφορικές; ποια διαδρομή πρέπει να ακολουθήσει ο καθένας;
ποια διαδρομή πρέπει να ακολουθήσει ο καθένας; και ο Στάθης τη διαδρομή
και ο Στάθης τη διαδρομή  ποιο θα είναι το σημείο συνάντησης τους;
ποιο θα είναι το σημείο συνάντησης τους;
 αρκεί η εξίσωση (1) να είναι ταυτότητα πράγμα που είναι αδύνατο (αφού είναι της μορφής
αρκεί η εξίσωση (1) να είναι ταυτότητα πράγμα που είναι αδύνατο (αφού είναι της μορφής  με
με 
 δεν είναι οριζόντιες οι συντελεστές διεύθυνσής τους είναι διάφοροι του μηδενός, δηλαδή ισχύει:
δεν είναι οριζόντιες οι συντελεστές διεύθυνσής τους είναι διάφοροι του μηδενός, δηλαδή ισχύει:  τότε
τότε και
και 



 έχουμε:
έχουμε:  και
και 

 και
και  οπότε
οπότε  όπως βρήκαμε (μην ξεχνάμε ότι και η τιμή
όπως βρήκαμε (μην ξεχνάμε ότι και η τιμή  ),
),

 οπότε το τρίγωνο ΚΛΜ είναι σκαληνό.
οπότε το τρίγωνο ΚΛΜ είναι σκαληνό. , όπου παριστάνει το εμβαδόν του τριγώνου ΚΛΜ
, όπου παριστάνει το εμβαδόν του τριγώνου ΚΛΜ θα είναι της μορφής:
θα είναι της μορφής: 

 τότε και το συμμετρικό του
τότε και το συμμετρικό του  ως προς τον
ως προς τον  θα είναι το σημείο
θα είναι το σημείο  το οποίο για να ανήκει στην
το οποίο για να ανήκει στην

![A_\lambda ,\,\,\,\lambda \in \left[ {1,10} \right] A_\lambda ,\,\,\,\lambda \in \left[ {1,10} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/7e796741b7a3ba66a1198f6c148e8c4f.png) και ο Στάθης τις διαδρομές
και ο Στάθης τις διαδρομές ![{\rm B}_\lambda ,\,\,\lambda \in \left[ {1,10} \right] {\rm B}_\lambda ,\,\,\lambda \in \left[ {1,10} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/1d02053cad535b93be1aa32e8cdc08c2.png) όπου λ φυσικός αριθμός. Αν "προσομοιώσουμε" τις διαδρομές
όπου λ φυσικός αριθμός. Αν "προσομοιώσουμε" τις διαδρομές  και
και  να απαντήσετε στα εξής:
να απαντήσετε στα εξής: δεν πρόκειται οι διαδρομές μας να είναι ανηφορικές αλλά ούτε για κάθε
δεν πρόκειται οι διαδρομές μας να είναι ανηφορικές αλλά ούτε για κάθε  θα είναι
θα είναι ) δεν θα συναντηθώ με το Μίλτο σου λέω ότι αν γυρίσεις το post στην 1η σελίδα θα δεις ότι στην 4η άσκηση (συγγραφέας είναι ο Μίλτος και λύτης εγώ) άρα έχουμε συναντηθεί
) δεν θα συναντηθώ με το Μίλτο σου λέω ότι αν γυρίσεις το post στην 1η σελίδα θα δεις ότι στην 4η άσκηση (συγγραφέας είναι ο Μίλτος και λύτης εγώ) άρα έχουμε συναντηθεί με
με  .
. με τους άξονες για τις διάφορες τιμές του πραγματικού αριθμού
με τους άξονες για τις διάφορες τιμές του πραγματικού αριθμού  να έχει δυο άνισες πραγματικές ρίζες
να έχει δυο άνισες πραγματικές ρίζες  με
με  .
. και
και  τις συναρτήσεις που προκύπτουν από την
τις συναρτήσεις που προκύπτουν από την 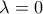 και
και  αντίστοιχα, να λυθεί η ανίσωση
αντίστοιχα, να λυθεί η ανίσωση  .
. να λυθεί η ανίσωση
να λυθεί η ανίσωση  .
. και
και  όταν ισχύει ότι
όταν ισχύει ότι  .
. έχουμε:
έχουμε: .
. . Είναι
. Είναι  .
. και επειδή
και επειδή  .
. τότε έχουμε ένα κοινό σημείο με τον άξονα των x
τότε έχουμε ένα κοινό σημείο με τον άξονα των x τότε δεν έχουμε κανένα κοινό σημείο με τον άξονα των x.
τότε δεν έχουμε κανένα κοινό σημείο με τον άξονα των x. η οποία έχει ένα σημείο τομής με τον άξονα των x και ένα με τον άξονα των y.
η οποία έχει ένα σημείο τομής με τον άξονα των x και ένα με τον άξονα των y. δύο πραγματικές και άνισες λύσεις πρέπει Δ>0 άρα
δύο πραγματικές και άνισες λύσεις πρέπει Δ>0 άρα  με
με  και για να είναι
και για να είναι  πρέπει
πρέπει  (διότι
(διότι  ). Όμως απο τύπους Vieta είναι
). Όμως απο τύπους Vieta είναι  . Άρα πρέπει και
. Άρα πρέπει και 
 . Επομένως
. Επομένως  .
. και για λ=-1 είναι
και για λ=-1 είναι  ενώ
ενώ  .
. γίνεται
γίνεται  \displaystyle{\left( { - x^2 + 2x - 3} \right)\left( { - 2x + 1} \right) \ge 0 \Leftrightarrow x \in \left( {\frac{1}{2}, + \infty } \right)
\displaystyle{\left( { - x^2 + 2x - 3} \right)\left( { - 2x + 1} \right) \ge 0 \Leftrightarrow x \in \left( {\frac{1}{2}, + \infty } \right) f\left( x \right) = 2x^2 + 2x + 3
f\left( x \right) = 2x^2 + 2x + 3 f^2 \left( x \right) \le 8x^3 + 12x + 29 \Leftrightarrow 4x^4 + 4x^2 + 9 + 8x^3 + 12x^2 + 12x \le 8x^3 + 12x + 29}
f^2 \left( x \right) \le 8x^3 + 12x + 29 \Leftrightarrow 4x^4 + 4x^2 + 9 + 8x^3 + 12x^2 + 12x \le 8x^3 + 12x + 29} .
. και βρίσκουμε
και βρίσκουμε  δεκτή ή
δεκτή ή  .
.![\left( {x^2 - 1} \right)\left( {x^2 + 5} \right) \le 0 \Leftrightarrow x \in \left[ { - 1,1} \right] \left( {x^2 - 1} \right)\left( {x^2 + 5} \right) \le 0 \Leftrightarrow x \in \left[ { - 1,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fb46ace360f1a6019ff4bd221c657631.png) .
. και επειδή
και επειδή  άρα
άρα  .
. λύνουμε το σύστημα
λύνουμε το σύστημα 

 κι επειδή
κι επειδή  .
. κι επειδή
κι επειδή  .
. δεκτή λύση.
δεκτή λύση. και ο Στάθης στην
και ο Στάθης στην  , οι τροχιές των κινήσεων τους ποτέ δεν συναντιούνται.
, οι τροχιές των κινήσεων τους ποτέ δεν συναντιούνται.
 κι επειδή
κι επειδή  .
. κουράζεται περισσότερο ο Μίλτος σε σχέση με τον Στάθη στις διαδρομές
κουράζεται περισσότερο ο Μίλτος σε σχέση με τον Στάθη στις διαδρομές  αντίστοιχα,
αντίστοιχα,
 ή
ή 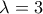

 ή
ή 
 .
. .
.
 δεκτή λύση.
δεκτή λύση.
 .
.