Επαναληπτική στην Παραβολή

Ιστοσελίδα · #1

Μια επαναληπτική άσκηση στην παραβολή

Δίνεται η παραβολή $\displaystyle{y^2 = 2px}$ με $\displaystyle{p > 0}$ και $\displaystyle{M(x_1 ,y_1 )}$ τυχαίο σημείο της με $\displaystyle{y_1 > 0}$ . Η εφαπτομένη από το Μ τέμνει τον άξονα x΄x στο σημείο $\displaystyle{E_x }$ και η κάθετος στο Μ τέμνει τον x΄x στο σημείο $\displaystyle{K_x }$ . Από το Μ φέρνουμε τις $\displaystyle{ MM_\Delta }$ , $\displaystyle{MM_{\rm X} }$ κάθετους στην διευθετούσα , και τον άξονα x΄x αντίστοιχα. 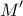Η $\displaystyle{ME}$ (Ε εστία της παραβολής ) τέμνει την παραβολή στο σημείο $\displaystyle{M'}$ και η κάθετος από το σημείο 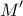$\displaystyle{M'}$ την δευθετούσα στο Σ. Να δείξετε ότι:

α) Το τετράπλευρο $\displaystyle{MM_\Delta E_X E}$ είναι ρόμβος.
β) Οι ευθείες $\displaystyle{ME_X }$ , yy΄ και $\displaystyle{EM_\Delta }$ συντρέχουν (Ε η εστία της παραβολής)
γ) Το ίχνος της καθέτου από την εστία προς την εφαπτομένη είναι σημείο του άξονα y΄y.
δ) Τα σημεία Ε και Ο (Ο κορυφή της παραβολής) είναι τα μέσα των $\displaystyle{E_X K_X }$ και $\displaystyle{E_X N_X }$ αντίστοιχα.
ε) Η κάθετος στο Μ διχοτομεί την γωνία $\displaystyle{EMK}$ όπου ΜΚ//x΄x.

Y. Σ Θα ακολουθήσουν και άλλα ερωτήματα

nightchild · #2

Για το α)

Έστω ε η εφαπτόμενη της παραβολής στο σημείο Μ τότε $\epsilon: yy_1=p(x+x_1)$
Το σημείο τομής της ε και του άξονα χ'χ ειναι το E_x(-x_1,0)

το $M_{\Delta}$ έχει συντεταγμένες $M_{\Delta}(-\frac{p}{2},y_1)$ και η εστία της παραβολής είναι $E(\frac{p}{2},0)$

Οι αποστάσεις $MM_{\Delta},EE_x$ είναι ίσες με $EE_x=\frac{p}{2}+x_1$
Όμως $MM_{\Delta}\parallel EE_x$ (διότι $MM_{\Delta},xx' \perp \delta$ )
Άρα $MM_{\Delta}E_xE$ παραλληλόγραμμο.
Έυκολα βρίσκουμε οτι $\lambda_{\epsilon}=\frac{p}{y_1} , \lambda_{M_{\Delta}E}=-\frac{y_1}{p}$ οπότε $\lambda_{\epsilon}\cdot \lambda_{M_{\Delta}E} = -1$
Επομένως οι διαγώνιες είναι κάθετες, Οπότε το $MM_{\Delta}E_xE$ είναι ρόμβος.

Ιστοσελίδα · #3

Για να μην ξεχαστεί η άσκηση παραθέτω την λύση του β ερωτήματος καθώς και ένα σχήμα

β) Οι συντεταγμένες του σημείου $\displaystyle{ {\rm M}_\Delta }$ είναι: $\displaystyle{ {\rm M}_\Delta \left( { - \frac{p}{2},y_1 } \right) }$

Οι διαγώνιες του ρόμβου τέμνονται στο μέσο της $\displaystyle{ E{\rm M}_\Delta }$ που έχει συντεταγμένες $\displaystyle{ \left( {\frac{{\frac{p}{2} - \frac{p}{2}}}{2},\frac{{y_1 + 0}}{2}} \right) = \left( {0,\frac{{y_1 }}{2}} \right) }$ και έχει τετμημένη μηδέν, άρα οι διαγώνιοι τέμνονται πάνω στον οριζόντιο άξονα, δηλαδή οι ευθείες $\displaystyle{ ME_x ,yy' }$ και $\displaystyle{ EM_\Delta }$ συντρέχουν.

Ιστοσελίδα · #4

Για να επανέλθει, υπολείπονται τα άλλα ερωτήματα

#5

καλημέρα...ας συνεχίσουμε

το γ) είναι φανερό αφού το $M_{\Delta}E_{x}EM$ είναι ρόμβος
το δ)
η $MK_{x}$ έχει εξίσωση: $y=-\frac{y_1}{p}x+\frac{y_1(x_1+p)}{p}$

το $K_x(x_1+p),E_X(-x_1,0),\,\,E(\frac{p}{2},0)\rightarrow E \mu\epsilon \sigma o \,\,\ E_xK_x$

$M_x(x_1,0),\,\,E_x(-x_1,0),\,\,O(0,0)\rightarrow O \mu\epsilon \sigma o \,\,\ E_x M_x$
το ε)...από την ανακλαστική ιδιότητα παραβολής

Ιστοσελίδα · #6

Άλλα δύο ερωτήματα στην επαναληπτική παραβολή

στ) Να δείξετε ότι το τετράπλευρο $\displaystyle{ M_\Delta MK_X E }$ είναι παραλληλόγραμμο,

ζ) Να βρεθεί ο γεωμετρικός τόπος των προβολών της εστίας Ε στην εφαπτόμενη στο σημείο $\displaystyle{ M(x_1 ,y_1 ) }$ , όταν το σημείο Μ διατρέχει την παραβολή.

Επαναληπτική στην Παραβολή

Επαναληπτική στην Παραβολή

Re: Επαναληπτική στην Παραβολή

Re: Επαναληπτική στην Παραβολή

Re: Επαναληπτική στην Παραβολή

Re: Επαναληπτική στην Παραβολή

Re: Επαναληπτική στην Παραβολή

Μέλη σε σύνδεση