 περιστρέφεται περί το
περιστρέφεται περί το  , ώστε η πλευρά
, ώστε η πλευρά  να διέλθει
να διέλθει από το σημείο
 . Βρείτε τις συντεταγμένες των σημείων
. Βρείτε τις συντεταγμένες των σημείων 
Συντονιστής: Τηλέγραφος Κώστας
 περιστρέφεται περί το
περιστρέφεται περί το  , ώστε η πλευρά
, ώστε η πλευρά  να διέλθει
να διέλθει  . Βρείτε τις συντεταγμένες των σημείων
. Βρείτε τις συντεταγμένες των σημείων 
Το σημείοKARKAR έγραψε:Το τρίγωνοπεριστρέφεται περί το
, ώστε η πλευρά
να διέλθει
από το σημείο. Βρείτε τις συντεταγμένες των σημείων
 είναι το ένα σημείο τομής των κύκλων
είναι το ένα σημείο τομής των κύκλων  και του κύκλου
και του κύκλου  διαμέτρου
διαμέτρου  με
με  (αφού
(αφού  και
και  των
των  και
και 

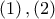 . Έχουμε:
. Έχουμε: 


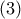 έχει
έχει  άρα έχει ρίζες τις
άρα έχει ρίζες τις  οπότε τα σημεία τομής των δύο κύκλων είναι:
οπότε τα σημεία τομής των δύο κύκλων είναι:  και προφανώς μιλάμε για το σημείο
και προφανώς μιλάμε για το σημείο  με
με  (το άλλο είναι το δεύτερο σημείο τομής των δύο αυτών κύκλων).
(το άλλο είναι το δεύτερο σημείο τομής των δύο αυτών κύκλων). η οποία διέρχεται από τα σημεία
η οποία διέρχεται από τα σημεία  και
και  που έχει συντελεστή διεύθυνσης
που έχει συντελεστή διεύθυνσης 
 . Το σημείο
. Το σημείο  είναι το ένα σημείο τομής με θετική τετμημένη
είναι το ένα σημείο τομής με θετική τετμημένη  και του κύκλου
και του κύκλου 



 το σημείο του τριγώνου
το σημείο του τριγώνου  που μετά την περιστροφή αντιστοιχίζεται στο σημείο
που μετά την περιστροφή αντιστοιχίζεται στο σημείο  ,
,  είναι εσωτερικό σημείο του
είναι εσωτερικό σημείο του  θα έχει συντεταγμένες
θα έχει συντεταγμένες  με
με  .
. γύρω από το σημείο
γύρω από το σημείο  τα τμήματα
τα τμήματα 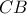 και
και 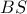 ταυτίζονται οπότε
ταυτίζονται οπότε 

 .
. γύρω από το σημείο
γύρω από το σημείο  τα τμήματα
τα τμήματα 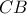 και
και 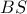 , τα τμήματα
, τα τμήματα  ,
,  , καθώς και τα τμήματα
, καθώς και τα τμήματα 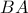 ,
,  ταυτίζονται οπότε
ταυτίζονται οπότε  ,
,  και
και  συνεπώς τα τρίγωνα
συνεπώς τα τρίγωνα  ,
,  και
και  είναι ισοσκελή με κορυφή το
είναι ισοσκελή με κορυφή το  , κι επειδή η γωνία της κορυφής
, κι επειδή η γωνία της κορυφής  είναι ίση σε κάθε τρίγωνο από αυτά λόγω της περιστροφής, τα τρία αυτά τρίγωνα είναι μεταξύ τους όμοια (αφού θα έχουν τρεις γωνίες ίσες μια προς μια).
είναι ίση σε κάθε τρίγωνο από αυτά λόγω της περιστροφής, τα τρία αυτά τρίγωνα είναι μεταξύ τους όμοια (αφού θα έχουν τρεις γωνίες ίσες μια προς μια).

 τότε
τότε 
 (1)
(1)



 αφού το σημείο
αφού το σημείο  ανήκει στο 1ο τεταρτημόριο
ανήκει στο 1ο τεταρτημόριο
 βρίσκονται οι συντεταγμένες του σημείου
βρίσκονται οι συντεταγμένες του σημείου  .
. είναι σύνθεση τριών μετασχηματισμών του επιπέδου, αρχικά παράλληλη μεταφορά του αρχικού τριγώνου κατά διάνυσμα
είναι σύνθεση τριών μετασχηματισμών του επιπέδου, αρχικά παράλληλη μεταφορά του αρχικού τριγώνου κατά διάνυσμα  , κατόπιν στροφή του τριγώνου γύρω από το
, κατόπιν στροφή του τριγώνου γύρω από το  κατά γωνία
κατά γωνία  με πίνακα στροφής
με πίνακα στροφής  και τέλος παράλληλη μεταφορά κατά διάνυσμα
και τέλος παράλληλη μεταφορά κατά διάνυσμα  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 1 επισκέπτης