 και την εστία της
και την εστία της  . Aν
. Aν  είναι μια μεταβλήτή εφαπτομένη της να βρεθεί ο γ.τ της προβολής της
είναι μια μεταβλήτή εφαπτομένη της να βρεθεί ο γ.τ της προβολής της  επι της εφαπτομένης
επι της εφαπτομένης  .
.Συντονιστής: chris_gatos
 και την εστία της
και την εστία της  . Aν
. Aν  είναι μια μεταβλήτή εφαπτομένη της να βρεθεί ο γ.τ της προβολής της
είναι μια μεταβλήτή εφαπτομένη της να βρεθεί ο γ.τ της προβολής της  επι της εφαπτομένης
επι της εφαπτομένης  .
.
Beautiful...maths-!!! έγραψε:Μια γεύση...
Εύκολο για όσους θυμούνται την ανακλαστική ιδιότητα των κωνικών τομών:erxmer έγραψε:Θεωρούμε τη έλλειψη/υπερβολήκαι την εστία της
. Aν (ε) είναι μια μεταβλήτή εφαπτομένη της να βρεθεί ο γ.τ της προβολής της
επι της εφαπτομένης (ε) .
 ως προς την εφαπτομένη στο
ως προς την εφαπτομένη στο  βρίσκεται στην ευθεία που συνδέει την άλλη εστία,
βρίσκεται στην ευθεία που συνδέει την άλλη εστία, 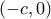 , και το
, και το  , και μάλιστα, λόγω συμμετρίας, σε απόσταση
, και μάλιστα, λόγω συμμετρίας, σε απόσταση  από το
από το 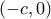 , ο ζητούμενος γεωμετρικός τόπος δεν είναι παρά ο παρακάτω:
, ο ζητούμενος γεωμετρικός τόπος δεν είναι παρά ο παρακάτω: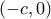 και ακτίνας
και ακτίνας  σημείο
σημείο  με τα σημεία επί του κύκλου είναι ... ο κύκλος κέντρου
με τα σημεία επί του κύκλου είναι ... ο κύκλος κέντρου  και ακτίνας
και ακτίνας  .
.  ως προς την εφαπτομένη στο
ως προς την εφαπτομένη στο  βρίσκεται στην ευθεία που συνδέει την άλλη εστία,
βρίσκεται στην ευθεία που συνδέει την άλλη εστία, 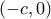 , και το
, και το  , και μάλιστα, λόγω συμμετρίας, σε απόσταση
, και μάλιστα, λόγω συμμετρίας, σε απόσταση  από το
από το 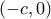 , ο ζητούμενος γεωμετρικός τόπος δεν είναι παρά ο παρακάτω:
, ο ζητούμενος γεωμετρικός τόπος δεν είναι παρά ο παρακάτω: 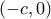 και ακτίνας
και ακτίνας  σημείο
σημείο  με τα σημεία επί του κύκλου είναι ... ο κύκλος κέντρου
με τα σημεία επί του κύκλου είναι ... ο κύκλος κέντρου  και ακτίνας
και ακτίνας  .
.  , ενώ και κάποια σχήματα θα βοηθούσαν...]
, ενώ και κάποια σχήματα θα βοηθούσαν...] 
Και θεωρία και πράξηmaths-!!! έγραψε:H θεωρία του Γιώργου Μπαλόγλου.

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες