 ο μικρότερος θετικός ακέραιος τέτοιος ώστε να υπάρχουν
ο μικρότερος θετικός ακέραιος τέτοιος ώστε να υπάρχουνθετικοί
 ώστε να ισχύει η ισότητα
ώστε να ισχύει η ισότητα  τότε να υπολογίσετε το λόγο
τότε να υπολογίσετε το λόγο 
Συντονιστής: chris_gatos
 ο μικρότερος θετικός ακέραιος τέτοιος ώστε να υπάρχουν
ο μικρότερος θετικός ακέραιος τέτοιος ώστε να υπάρχουν ώστε να ισχύει η ισότητα
ώστε να ισχύει η ισότητα  τότε να υπολογίσετε το λόγο
τότε να υπολογίσετε το λόγο 
 δεν υπάρχουν θετικοί
δεν υπάρχουν θετικοί  ώστε
ώστε  διότι τότε
διότι τότε 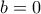 , άτοπο.
, άτοπο. η ισότητα γίνεται τελικά
η ισότητα γίνεται τελικά  που δε δίνει θετικούς
που δε δίνει θετικούς  .
. .
. παίρνουμε διαδοχικά
παίρνουμε διαδοχικά  που δίνει τελικά
που δίνει τελικά  δηλαδή
δηλαδή  δηλαδή
δηλαδή 
 ,
,  και
και  έχουμε
έχουμε  άρα τελικά έχουμε το ζητούμενο:
άρα τελικά έχουμε το ζητούμενο: 
 βρίσκουμε
βρίσκουμε  που είναι αδύνατον να βρούμε τον λόγο που ζητάμε
που είναι αδύνατον να βρούμε τον λόγο που ζητάμε έχουμε
έχουμε  και από εδώ βρίσκουμε
και από εδώ βρίσκουμε  και άρα
και άρα 
 δεν δίνονται ακέραιοι)
δεν δίνονται ακέραιοι)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες