Bulletin Επανάληψη ΓΛ ΣΥΝΑΡΤ. ΟΡΙΑ ΣΥΝΕΧΕΙΑ

parmenides51

Θεωρώ πως είναι χρήσιμο να έχουμε ένα bulletin (ευρετήριο) με τις ασκήσεις και τα διαγωνίσματα ανά κεφάλαιο και στα Μαθηματικά Γ΄Λυκείου Κατεύθυνσης καθώς και με τις συλλογές ασκήσεων επαναληπτικού χαρακτήρα, ένα σε κάθε φάκελο ώστε να διευκολυνθεί η αναζήτηση τους από τον εκάστοτε ενδιαφερόμενο.
Θα ανανεώνω την παρούσα δημοσίευση ώστε να παραμένουν όλα τα links στην 1η σελίδα.
Θα συμπληρώνω και τυχόν ενδιαφέρουσες συλλογές ασκήσεων προσπαθώντας να είμαι όσο γίνεται πιο αντικειμενικός στην κρίση.
Στην παρούσα δημοσίευση συμπεριλαμβάνεται η συντριπτική πλειοψηφία των σχετικών δημοσιεύσεων.
Η σειρά είναι αυστηρά χρονολογική. Τελευταία άσκηση: 01/08/2012 (φάκελος: Συναρτήσεις Ορια Συνέχεια) 31/12/2011 (λοιποί φάκελοι)
Αναλυτικά οι ενημερώσεις εδώ.

Χρησιμοποιούνται οι φάκελοι:
Συναρτήσεις Όρια Συνέχεια, Ασκήσεις μόνο για μαθητές, Θέματα με απαιτήσεις, ΑΣΕΠ: Προτεινόμενα Θέματα Μαθηματικών, Φάκελος του Καθηγητή: Ανάλυση.

Όλα τα μαθήματα: Bulletin Ευρετήριο
ΑΓΥΜΝ , ΒΓΥΜΝ , ΓΓΥΜΝ , ΑΛΑΛΓ (πρόοδοι), ΑΛΓΕΩ , ΒΛΑΛΓ (συστήματα), ΒΛΓΕΩ , ΒΛΚΑΤ , ΓΛΓΕΝ , ΓΛ ΜΙΓΑΔ , ΓΛ ΣΥΝΑΡΤ, ΓΛ ΔΙΑΦΟΡ, ΓΛ ΟΛΟΚΛ, ΓΛK ΕΠΑΝ

Τράπεζα Θεμάτων Γυμνασίου - Λυκείου (mathematica.gr)

Διαγωνίσματα
2008 από Κώστα Τηλέγραφο
2008 από Χρήστο Καρδάση
2009 από Χρήστο Καρδάση
2009 Ι από Θωμά Ραϊκόφτσαλη
2009 ΙΙ από Θωμά Ραϊκόφτσαλη
2009 από Σπύρο Καπελλίδη
2010 από xgastone
2010 από Θωμά Ραϊκόφτσαλη (+ μιγαδικοί)
τεστ 2010 από Νίκο Μαυρογιάννη
2010 από Νίκο Μαυρογιάννη
2011 από Κώστα Σερίφη
2011 από Βασίλη Κακαβα (+ μιγαδικοί)
2011 από wavelet
2011 από Βασίλη Κακαβα
2011 από Βασίλη Στεφανίδη
2011 από wavelet
2011 από Βασίλη Στεφανίδη
2011 από Σπύρο Καπελλίδη (+ μιγαδικοί)
2011 από KARKAR
2011 από Νίκο Μαυρογιάννη
2012 από Γιώργο Τσικαλουδάκη
2012 από Νίκο Μαυρογιάννη
τεστ 2012 από erxmer (+ μιγαδικοί)
2012 από Χρήστο Καρδάση (+ μιγαδικοί)
2012 από Βασίλη Στεφανίδη
2013 από Νίκο Αλεξανδρόπουλο (+ μιγαδικοί)

Φυλλάδια πριν την Γ'
προαπαιτούμενες γνώσεις για τα μαθηματικά γ' λυκείου (συζήτηση)
χρήσιμες γνώσεις μαθηματικών του Ιγνάτιου Ιωαννίδη
επαναληπτικό φυλλάδιο α΄β΄ λυκείου για γ΄λυκείου από polysot
πριν τη γ λυκείου – τυπολόγιο μαθηματικών από Μίλτο Παπαγρηγοράκη
30 απαραίτητες ανισώσεις - εξισώσεις από Δημήτρη Μυρογιάννη

Ερωτήσεις για πεδίο ορισμού, σύνολο τιμών, πράξεις συναρτήσεων
συναρτήσεις 01 από Θωμά Ραϊκόφτσαλη
ίσες συναρτήσεις από polysot
απορία από Maria Nikolaou
περιορισμοί συνάρτησης από Κώστα Χαροκόπο
σωστό ή λάθος? από Linardatos
ερώτηση από Eukleidis
ισότητα συναρτήσεων από Γιώργο Απόκη
η σχέση f(x)g(x)=0 από Ardid
ανισοτική σχέση με συνάρτηση από Ardid
απορίες για το πεδίο ορισμού από Ardid
επί συναρτήσεις από Σπύρο Καπελλίδη (θεωρητική)
πεδίο ορισμού από Θωμά Ποδηματά
2 ερωτήσεις για τα μαθηματικά κατεύθυνσης από Δημήτρη Κατούνη

Περιοδική
$\displaystyle{f(x+1)f(x)+f(x+1)+1=f(x)}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x) = \eta \mu (\alpha x) + \eta \mu (\beta x)}$ από Αντώνη Κυριακόπουλο
$\displaystyle{f(x+y)+f(x-y)=2f(x)f(y), \exists x_{0} : f(x_{0})=-1}$ από Φωτεινή Καλδή
$\displaystyle{f(x+a)=\frac{1}{2}+}\sqrt{f(x)-\big(f(x)\big)^2}}$ από Φωτεινή Καλδή
$\displaystyle{f(x+2)=f(x+1)-f(x)}$ από Γιώργος Κ77

Πεδίο ορισμού
$\displaystyle{f\left( x\right) =\sqrt{1-x^{4}},g\left( x\right) =\frac{x-1}{1-\alpha -x^{2}}}$ από Νίκο Μαυρογιάννη
$\displaystyle{f\left(x \right)=ln\left(x+\sqrt{x^{2}+1} \right)}$ από christodoulou
$\displaystyle{f(x)=x^x}$ από BGNMK
$\displaystyle{f(x) = {\log _{\sqrt 3 - 1}}\left( {7 - 2 \sqrt x - x} \right)}$ από nonlinear
$\displaystyle f(x)=ln(-x^2+7x-10)+3\sqrt{cos(\pi\sqrt{x^2+7})-1}-ln2$ από Παναγιώτη Γκριμπαβιώτη
$\displaystyle{f(x)=\sqrt{4\lambda x^2-4x+1},\lambda \in R}$ από Γιώργο Απόκη
$\displaystyle{f(x) = \sqrt {{x^{\ln x}} - e} }$ από solars
$\displaystyle{f(x) = \sqrt {4 - \sqrt {5 + 2x} } }$ από solars
$\displaystyle{f(x)=\sqrt{-x^2+(a-3)x-a^2},a\in R}$ από Θεοχάρη Κιβριδάκη
$\displaystyle{f(x)=\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}}$ από KARKAR

Συμμετρίες
$\displaystyle{f\left( x \right) \le g\left( x \right),f\left( {x + y} \right) \le f\left( x \right) + f\left( y \right),g}$ περιττή από Βασίλη Μαυροφρύδη (mathxl) (περιττή)
$\displaystyle{f(x) = \frac{2x - 1}{4x + 2}}$ από irakleios (κέντρο συμμετρίας)
$\displaystyle{f(xf(y))=yf(x)}$ από socrates (περιττή)
$\displaystyle{f(x+y)=(fof)(x)+(fof)(y),f}$ άρτια από Γιώργος Κ77

Σύνολο τιμών
$\displaystyle{f(x) = \sin x \sin (x + 2) - \sin ^2 (x + 1)}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x)=\frac{2x}{1+x^{2}}}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{f(x) =\frac{x^{2}-2x+\lambda }{x^{2}+2x+\lambda }, f ( A_{f} ) =\left [\frac{1}{3} , 3\right],\lambda>1? }$ από Στράτο Παπαδόπουλο
$\displaystyle{f(x) = \frac{{x^2 - \lambda x + 1}}{{x^2 + x + 1}},f ( A_{f} )=[-3,3],\lambda=?}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle f(x)=\frac{x^{2}-x+1}{x^2+x+1}$ από KARKAR
$\displaystyle{f(x)=\frac{1+sin2x}{5+4cos2x},x \in \left(-\frac{\pi}{2},\frac{\pi}{2}\right)}$ από Γιώργο Απόκη
$\displaystyle{f(x) = 2 - x - x^5}$ από pastavr
$\displaystyle{f(x) =\frac{x^2 - \mu x + 4}{x^2 - 2x + 4}}, f ( A_{f} ) =\left [ -1, \frac{5}{3}\right],\mu =? }$ από gian7
$\displaystyle{f(x) = \frac{x^2 + ax + b}{x^2 + 2x + 3}}, ( A_{f} ) =[-5,4],a^2 + b^2=?}$ από irakleios
$\displaystyle{{f\left( x \right) = \frac{{x^2 - l}} {{x^2 - 4x + 1 - l}}, f ( A_{f} ) =R,l =? }$ από Σωτήρη Λουρίδα

Τιμή συνάρτησης
$\displaystyle{f\left( x \right) = {x^3} - 6{x^2} + 17x,f\left( \alpha \right) = 16,f\left( \beta \right) = 20, \alpha+\beta=?}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f\left( x \right) = {x^3} - 3{x^2} + 5x,f\left( \alpha \right) = -2004,f\left( \beta \right) = 2010, \alpha+\beta=?}$ από christodoulou
$\displaystyle{f\left( x \right) ={2^{\eta {\mu ^2}x}} {3^{\sigma \upsilon {\nu ^2}x}} - {3^{\eta {\mu ^2}x}} {2^{\sigma \upsilon {\nu ^2}x}},f\left( \alpha \right) = \frac{1}{{2010}},f\left( \beta \right) = - \frac{1}{{2010}}, \alpha+\beta=?}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x)=\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}}$ από KARKAR
$\displaystyle{f^3(x)-f^2(x)+f(x)+e^x+2008=0}$ από HoliC

Πράξεις συναρτήσεων
νδο $\displaystyle{\left| {af(x) + \beta g(x)} \right| \le \sqrt {a^2 + \beta ^2 },\frac{{f^8 (x)}}{{a^3 }} + \frac{{g^8 (x)}}{{\beta ^3 }} = \frac{1}{{\left( {a + \beta } \right)^3 }}}$ όταν $\displaystyle{\frac{{f^4 (x)}}{a} + \frac{{g^4 (x)}}{\beta } = \frac{1}{{a + \beta }}f^2 (x) + g^2 (x) = 1}$ από Στράτο Παπαδόπουλο
$\displaystyle{g^3(x)=x,g=?}$ από xgastone
νδο $\displaystyle{f=g}$ όταν $\displaystyle{x_{1}<x_{2}<x_{3}\Rightarrowf(x_{1})f(x_{2})f(x_{3})=g(x_{1})g(x_{2})g(x_{3})\neq 0}$ από Δημήτρη Ιωάννου
νδο $\displaystyle{ \exists a>0 : a[f(\frac{9}{a})-2011a^{2}]>26}$ όταν $\displaystyle{|f(x)-3x|\leq 1}$ από Γιώργος Κ77
$\displaystyle{f(x)= 2x+3, g(x)= \frac{2kx^3+x^2-k^2x+3k}{x^2-kx+1},k=?, f=g}$ από dimitrisman

Δεν υπάρχει συνάρτηση
$\displaystyle{f(x)+f(1-x)=x}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{2f(x+y)=f(x+2y)+x^{3}}$ από Αναστάσιο Κοτρώνη
$\displaystyle{f(\eta \mu \theta )=\sigma \upsilon \nu \theta }$ από paganini
$\displaystyle{|f(x)-f(y)|>1,x\neq{y}}$ από mathxl
$\displaystyle{2 f(x+y)=f(x+2y)+x^3}$ από Φωτεινή Καλδή
$\displaystyle{ f\left(x + \frac{1}{x}\right) = x^2 - 3x + 5, x > 0}$ από Αντώνη Σπυριδάκη
$\displaystyle{f(f(x))=x^{2}-2}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(f(x))=\left\{\begin{array}{l}\sqrt{2010},x\in Q \\ 2010,x\in R-Q\end{array}\right}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x)g(y)=x+y}$ από Κωνσταντίνα Κυριακοπούλου
$\displaystyle{f(\eta \mu \theta )=\eta \mu2 \theta }$ από papel
$\displaystyle{f(x)f(y) = f(x+y) - xy}$ από irakleios
$\displaystyle{x^3+x^2(1-2y)+xy(y-2)+y^2 \leq f(x)-f(y) \leq x^3-2x^2(1+y)+xy(4+y)-2y^2}$ από erxmer
$\displaystyle{f(f(x)) + xf(x) = 1}$ από socrates
$\displaystyle{f(ax+b)-f\left(\frac {1}{x}\right)=x^2+1, b \ge a-1 \ge 0,x \in [-1,1]-\{0\}}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)+g(y)=xy}$ από dimitrisbaltas
$\displaystyle{f(x)g(y)=x+y}$ από dimitrisbaltas
$\displaystyle{-x^2\leq f^2(x)-xf(x)\leq 3x^2-4x+1}$ από achilleas
$\displaystyle{f( - x) =- f(x), f\Big(\frac {1}{x + y}\Big) = f\Big(\frac {1}{x}\Big) + f\Big(\frac {1}{y}\Big) + 2(xy - 1000)}}$ $\displaystyle{,x, y\ne 0,x + y\ne 0}$ από socrates

Συναρτησιακή δεδομένο - συναρτησιακή ζητούμενο
νδο $\displaystyle{|f(x)-f(y)| = x-y}$ αν $\displaystyle{|f(x)-f(y)| \geq x-y}$ από Χρήστο Κυριαζή (chris_gatos)
νδο $\displaystyle{f(x+y)=f(x)+f(y)}$ αν $\displaystyle{f(x^{2}+y^{2})=xf(x)+yf(y)}$ από Αναστάσιο Κοτρώνη
νδο $\displaystyle{| f(x)-f(y)| \leq f(x-y)}$ αν $\displaystyle{f(x+y)\leq f(x)+f(y),f}$ άρτια από Μάνο Μανουρά
νδο $\displaystyle{\frac{f(x)+f(y)+f(w)}{3}= f(\sqrt[3]{xyw})}$ αν $\displaystyle{\displaystyle{\frac{f(x)+f(y)}{2}=f(\sqrt{xy})}}$ από Φωτεινή Καλδή
νδο $\displaystyle{f(xy)=xyf(1)}$ εαν $\displaystyle{f(x+y)=f(x)(1+y)}$ από Pla.pa.s
νδο $\displaystyle{f(f(x))=x}$ αν $\displaystyle{f(x+y)+f(f(x)+f(y)) = f(f(x+f(y))+f(y+f(x))),f \downarrow}$ από socrates (ενελικτική)
νδο $\displaystyle{f(ax)=\left|a \right|f(x)}$ αν $\displaystyle{f(ax)\leq \left|a \right|f(x)}$ από Δημήτρη Ιωάννου
νδο $|f(x)| \le |x|$ εαν $2f^{3}(x) +2f(x)=sinf(x) +x^{2}$ από Christiano
νδο $\displaystyle{f(2x) = 2f(x)}$ αν $\displaystyle{f(x+f(y))+f(f(x)+y)=2x+2y}$ από socrates
νδο $\displaystyle{|f(x)| \leq |x|}$ αν $\displaystyle{|f(x) - f(y) | \leq |x-y| ,f(f(f(0))) = 0}$ από socrates

Συναρτησιακή εξίσωση - εύρεση συνάρτησης
$\displaystyle{2f(x+y)=f(x+2y)+x^{3}}$ από Αναστάσιο Κοτρώνη
$\displaystyle{f(x+y)=f(x)f(a-y)+f(y)f(a-x),f(0)=\frac{1}{2}$ από Αναστάσιο Κοτρώνη
$\displaystyle{f(\eta \mu \theta )=\sigma \upsilon \nu \theta }$ από paganini
$\displaystyle{x f(x) = (x - 3) f(x + 1),f(2000) = 1999 \cdot 1998 \cdot 1997}$ από Χρήστο Καρδάση
$\displaystyle{ f(x+y+1)=(\sqrt{f(x)}+\sqrt{f(y)})^{2}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x)+f\left(\frac{1}{1-x}\right) =\frac{2(1-2x)}{x(1-x)}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{ x^{2}f(x)+f(1-x)=2x-x^{4}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(xyz)=xf(x)+yf(y)+zf(z)}$ από socrates
$\displaystyle{2 f(x+y)=f(x+2y)+x^3}$ από Φωτεινή Καλδή
$\displaystyle{f\left(\frac{5x-9}{4}\right)=5x+3}$ από tsolis
$\displaystyle{f\left( {f(x)} \right) = \frac{1}{{f\left( {\frac{1}{x}} \right)}}}$ από papel
$\displaystyle{f(x) + f(x^2 ) = f(\frac{1}{x}) + f(\frac{1}{{x^2 }}),x \ne 0}$ από chris_gatos
$\displaystyle{f(f(x))=-x}$ από Σπύρο Καπελλίδη
$\displaystyle{3f\left(\frac{1}{x}\right) + \frac{{2f(x)}}{x} = x^2}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x) = x[f(-x) - 1]}$ από ctheofi
$\displaystyle{ f(x) f\left(f(x)+\frac{1}{x}\right)=1,f(x)>\frac{1}{2x},x>0,f \downarrow}$ από Φωτεινή Καλδή
$\displaystyle{f(2 - x) f^2 (x + 1) = e^{x + 4} }$ από Γιώργο Τσικαλουδάκη
$\displaystyle{f(x)-f(y)=(x-y)f(x)f(y)}$ από Σπύρο Καπελλίδη
$\displaystyle{f(f(x)) + f(f(y)) = 2y +f(x-y)}$ από Μπάμπη Στεργίου
$\displaystyle{f(x)f(y) = f(x+y) - xy}$ από irakleios
$\displaystyle{f\left( x \right) + 2f\left( {\frac{{2002}}{x}} \right) = 3x}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x)=\begin{cases} \ x& ,x\geq 25 \\ \ f^2(50-x)-24x &, x<25 \end{cases}}$ από Παναγιώτη Γκριμπαβιώτη
$\displaystyle{\left| {f\left( x \right) - f\left( y \right) - x + y} \right| < \left| {x - y} \right|,x \ne y}$ , $\displaystyle{f\left( {f\left( x \right) - 2x} \right) = 2f\left( x \right) - 3x,f}$ περιττή από Νίκο Ζανταρίδη
$\displaystyle{f\left(f^2\left(x \right) \right+f^2\left(y \right))=\sqrt{x+y}}$ από Νίκο Ζανταρίδη
$\displaystyle{(f(x)-x )^{3}+x^{2}f(x)=3x^{3}}$ από Γιάννη Στάμου (propaid)
$\displaystyle{ (1 + yf(x))(1 - yf(x + y)= 1 ,x,y >0, f(x)>0}$ από socrates
$\displaystyle{f(a+x)+\lambda f(b-x)=g(x)}$ από Γιώργο Απόκη
$\displaystyle{\left(f\circ f \right)(x)=4x-9,\left(f\circ f\circ f \right)(x)=8x+\alpha}$ από Βασίλη Ευαγγέλου (vasilis.volos.13)
$\displaystyle{f(x+y)=f(x)f(a-y)+f(y)f(a-x),f(0)f(a)>0}$ από Δημήτρη Ιωάννου
$\displaystyle{(3-2x)f(x-1)+(x+1)f(1-x)=1-x}$ από Νίκο Ζαφειρόπουλο
$\displaystyle{f\left( \frac{x+1}{x-2} \right) + 2 f\left( \frac{x-2}{x+1} \right) =x}$ από Nazgul
$\displaystyle{f(f^2(x)+f(y))=xf(x) + y}$ από Μπάμπη Στεργίου
$\displaystyle{f\left( x \right) = x {2^x},x \in \left[ {0,2} \right)}$ , $\displaystyle{f\left( {x + 2} \right) = 4f\left( {x + 1} \right) - 4f\left( x \right)}$ από Νίκο Ζανταρίδη
$\displaystyle{f(x)+2f(1-x)=13 - 2x}$ από marmix (γραφική λύση από κώστα Δόρτσιο)
$\displaystyle{f\displaystyle{(x+y)=f(x)+f(y)}}$ ή $\displaystyle{{f(xy)=f(x)f(y)}}$ (διαζευκτικά) από Pla.pa.s
$\displaystyle{f(x+y)+f(x-y)=2f(x)+f(y)}$ από akis15
$\displaystyle{xf\left(\frac{x}{a}\right)-f\left(\frac{a}{x}\right)=b,x \ne 0, a\ne 0}$ από socrates
$\displaystyle{2f(x)+f(-x)=\left\{\begin{array} \ -x-3, \ x\leq 1 \\ \ x+3, \ \ x>1\\ \end{array}\right}$ από dennys
$\displaystyle{xf(xy)+f(-y)=xf(x),x,y \ne 0}$ από socrates
$\displaystyle{f(x + f(y + z)) + f(f(x + y) + z) = 2y}$ από socrates
$\displaystyle{f(x+y)+f(xy)=f(x^{2})+f(y^{2})}$ από socrates
$\displaystyle{f(x)f(y)+f\left(\frac{a}{x}\right)f\left(\frac{a}{y}\right) =2f(xy) ,x,y ,a>0,f(a)=1}$ από socrates
$\displaystyle{f (x+y )\ =\ f (x ) e^{f(y)\ -\ 1}}$ από socrates
$\displaystyle{g(xy+2x+g(x))=yg(x)}$ από socrates
$\displaystyle{f(x^2+y^2+2012xy)=x^2+y^2+2012f(x)f(y)}$ από socrates
$\displaystyle{f(x+y)+x^2+y^2=f(x^2+y^2)+x+y}$ από socrates
$\displaystyle{f(x^2y+f(x+y^2))=x^3+y^3+f(xy)}$ από socrates
$\displaystyle{x^2f(y)+yf(x^2)=f(xy)+a}$ από socrates
$\displaystyle{f(x+y) = f(x^{2012})+f(y^{2012})}$ από socrates
$\displaystyle{x(f(x)+f(y))=f(x)f(x+y)}$ από socrates
$\displaystyle{f(x+y)=f(x)+f(y)+f(xy)}$ από socrates

Συναρτησιακή εξίσωση - υπολογισμός τιμής
$\displaystyle{f(x)f\left( {f(x) + \frac{1}{x}} \right) = \frac{1}{2}}$ , $\displaystyle{f(1)=?}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{(fof)(x) = x^2 - 3x + 4}$ , $\displaystyle{f(2)=?}$ από ioakim
$\displaystyle{f(f(x))=4x+9}$ , $\displaystyle{f(-3)=?}$ από cospash
$\displaystyle{f(x)=\left\{\begin{matrix} 0 &,x=1\\ 2x - 2&,x \ge 1 \end{matrix}\right}}$ , πλήθος ριζών της $\displaystyle{f(f(f(f(x)))) = x}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x+y)+f(x-y) =2[f(x)+f(y)],f(1)=1}$ , $\displaystyle{f\left(\frac {22}{7}\right)=?}$ από Μπάμπη Στεργίου
$\displaystyle{|f(a)-f(b)|<|a-b|,f(f(f(0)))=0}$ , $\displaystyle{f(0)=?}$ από Χρήστο Στραγάλη
$\displaystyle{f(x) = x^2-2x}$ , $\displaystyle{ f(f(f(f(c))))=3,c=?}$ από Stuart Clark
$\displaystyle{ f(f(x))=x^{2}-x+1}$ , $\displaystyle{f(0)=?}$ από socrates
$\displaystyle{\left( {f \circ f} \right)\left( x \right) = \frac{{3x + 1}}{{x + 3}}}$ , $\displaystyle{f(-1),f(1)=?}$ από Atemlos
$\displaystyle{g(17 + x) = g\left( {17 - x} \right)}$ ,ρίζες $\displaystyle{{\rho _1},{\rho _2},{\rho _3}}$ , $\displaystyle{{\rho _1} + {\rho _2} + {\rho _3}=?}$ από Atemlos
$\displaystyle{f(x^{2}+x+3)+2\cdot f(x^{2}-3x+5) = 6x^{2}-10x+17}$ από socrates
$\displaystyle{4f(f(x)) = 2f(x) + x}$ , $\displaystyle{f(0)=?}$ από socrates
$\displaystyle{f(x)-f(y)=f(x)f\left(\frac{1}{y}\right)-f(y)f\left(\frac{1}{x}\right),x,y\ne 0}$ από socrates
$\displaystyle{4f(f(x))-2f(x)-3x=0}$ , $\displaystyle{f(0)=?}$ από socrates
$\displaystyle{(f \circ f \circ f)(x)=x^2-2x+2}$ , $\displaystyle{f(1)=?}$ από socrates

Συναρτησιακή εξίσωση με ερωτήματα
$\displaystyle{f(x+y)=f(x)+f(y)}$ από Σπύρο Ορφανάκη
$\displaystyle{f({x^2} + {y^2}) = x f(x) + y f(y)}$ από Χρήστο Καρδάση
$\displaystyle{f(f(x)) = x^2-x+1}$ από Μπάμπη Στεργίου
$\displaystyle{f(xy)=f(x)f(y)}$ από HoliC

Συναρτησιακή εξίσωση - περίεργη
$\displaystyle{f(x+y) = f(x)+f(y), xy>0, f}$ περιττή από Μπάμπη Στεργίου
$\displaystyle{f(f(n)) =-n}$ από Λευτέρη Πρωτοπαπά
νδο $\displaystyle{f(ab) = f(a) + f(b), a,b > 0}$ εαν $\displaystyle{x, bx, b^{2}x, ...}$ ΓΠ και $\displaystyle{f(x), f(bx), f(b^{2}x), ...$ ΑΠ $\displaystyle{f(1)=0}$ από Στράτο Παπαδόπουλο
νδο $\displaystyle{f(r x)=rf(x),r\in{Q},x\in{R}[}$ όταν $\displaystyle{f(a+b)=f(a) + f(b),a,b\in R}$ από katsanetrino
νδο $\displaystyle{f\left(c \right)\neq c}$ όταν $\displaystyle{f\left(g\left(x \right) \right)=g\left(f\left(x \right) \right),2\left[f\left(g\left(x \right) \right) \right]^{4}+2=\left(g\left(x \right) \right)^{4}+g\left(x \right)^{3}}$ από Σπύρο Ορφανάκη
$\displaystyle{ x+f(y)=af(y+f(x)),a=?}$ από socrates
$\displaystyle{f(1)=2,A(a,f(a)+a), B(b,f(b)+b) C(0,ab)}$ συνευθειακά από Βασίλη Μαυροφρύδη (mathxl)
νδο $\displaystyle{f(nk)=0 }$ εαν $\displaystyle{f(x+y)+f(x-y)=2(f(x)+f(y)),f(k)=0}$ από Γιώργος Κ77
νδο $\displaystyle{f=g}$ εαν $\displaystyle{f(\alpha )+f(\beta )=g(\alpha )+g(\beta ,\alpha \neq \beta}$ από Γιώργος Κ77

Συναρτησιακή ανίσωση
$\displaystyle{(x^2 + 1)f(x) \le 2x}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{f(xy)\le xf(y)}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f\left( x-\frac{b}{a}\right)+2x\leq\frac{a}{b} x^{2}+\frac{2b}{a}\leq f\left( x+\frac{b}{a}\right)-2x}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f\left(x^3+3x^2+3x \right)\leq x\leq f^{3}\left(x \right)+3f^{2}\left(x \right)+3f\left(x \right)}$ από Σπύρο Ορφανάκη
$\displaystyle{ f(x^{3}+x)\leq x\leq\bigl(f(x)\bigr)^{3}+f(x)}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x)\leq x,f(x+y)\leq f(x)+f(y)}$ από Silver
$\displaystyle{\left| {f(x) - f(y)} \right| \ge \left| {x^2 \ln x - y^2 \ln y} \right|,x,y \in \left[ {1,e} \right]}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{2 f(x)-g(x)=f(y)-y,f(x) g(x)\geq x+1}$ από socrates
$\displaystyle{f(x+y)\leq f(xy) }$ από socrates
$\displaystyle{|xf(y)-yf(x) |\leq 2,f(1)=2}$ από Πέτρο Χρονόπουλο (Μαθηματικός)
$\displaystyle{f(x)+f(y)\geq 2f(x+y)}$ από socrates
$\displaystyle{f(\frac{x}{e})\leq \ln x\leq f(x)-1 , x>0}$ από HoliC
$\displaystyle{f(xy){\ge}f(x)+f(y){\ge}\frac{\ln(xy)}{1+|\ln x{\cdot} \ln y|} , x,y>0}$ από socrates
$\displaystyle{f(x)\leq 4+2009x,f(x+y)\leq f(x)+f(y)-4}$ από socrates

Ερωτήσεις για σύνθεση
Εικασίες Νο 1 , Νο 2 , Νο 3 , Νο 4 , Νο 5 , Νο 6 από Ανδρέα Πούλο
αν fog 1-1, τότε f 1-1; από Γιώργο Τσικαλουδάκη
σύνθεση και πράξεις συναρτήσεων από maths-!!!

Σύνθεση συναρτήσεων
$\displaystyle{f ( f ( x ))=2009e^x -2009}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(\eta \mu \theta )=\sigma \upsilon \nu \theta }$ από paganini
$\displaystyle{f(f(x))=\left\{\begin{array}{l}\sqrt{2010},x\in Q \\ 2010,x\in R-Q\end{array}\right}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(f(x))=x^{2}-(2a-1)x+a^{2},f(k)=k}$ από Χρήστο Στραγάλη
$\displaystyle{g(x)=x^{2}+ax+b,fog=gof,f(k)=k}$ από Χρήστο Στραγάλη
$\displaystyle{f(x)=-x^{2},(gof)(x)=\sqrt{1+x^{2}},g=?}$ από christodoulou
$\displaystyle{ f(x)=\frac{\sqrt{3}x-1}{x+\sqrt{3}},\mathop {f\left( {f\left( {f \ldots \left( x \right)} \right)} \right) = x}\limits_{n - \varphi o\rho \varepsilon \varsigma } },n_{min}=?}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f\left( x\right) =x+\sqrt{x^{2}-4},g\left( x\right) =x+\frac{1}{x},f\circ g=?}$ από teotyre
$\displaystyle{{\left( {g(x)} \right)^5} = 9x,{\left( {g\left( {g(x)} \right)} \right)^{125}}=?}$ από nonlinear
$\displaystyle{ f(x)=min\left\{4x+1,x+2,-x+2 \right\}}$ από Χρήστο Στραγάλη (συνάρτηση min)
$\displaystyle{2f(xy)=f(x)f(y)+x^ny^n,f}$ 1-1 από Παναγιώτη Γκριμπαβιώτη
$f(x) = \left\{ \begin{array}{l} x + 4& ,x \ge 0 \\ \\ x - 2& ,x < 0 \\ \end{array} \right.{\rm{ }}{\rm{, g}}(x) = \left\{ \begin{array}{l} x - 4& ,x \ge 0 \\ \\ x + 2& ,x < 0 \\ \end{array} \right}$ από Γιώργο Τσικαλουδάκη
$\displaystyle{f(x) = \left\{ {\begin{array}{*{20}c} {2,x \in \left[ {0,1} \right]} \\ {1,x \in \left( { - \infty ,0} \right) \cup \left( {1, + \infty } \right)} \\ \end{array}} \right}, f(x^2 ) , f(1 - x) =?}$ από Νίκο Ζανταρίδη
$\displaystyle{f(x) = ax+b|x|,g(x) = ax-b|x|, f(f(x))=x\Rightarrow g(g(x))=x}$ από socrates
$\displaystyle{\left(f\circ f \right)(x)=4x-9,\left(f\circ f\circ f \right)(x)=8x+\alpha}$ από Βασίλη Ευαγγέλου (vasilis.volos.13)
$\displaystyle{f(x) = 3x-1+| 2x+1|,g(x) =\frac{1}{5}\left( 3x+5-|2x+5|\right)}$ από socrates
$\displaystyle{\left(f\circ g\right)\left(x\right)=\sqrt{1+x^2}, g\left(x\right)=-x^2.f=?}$ από Αντώνη Νασιούλα
νδο $\displaystyle{f=g}$ εαν $\displaystyle{f \circ f=g , g\circ g=f,f,g}$ γν. μονότονες από Σπύρο Καπελλίδη
$\displaystyle{(f\circ g)(x)=4-lnx,f(x)=e^x+2,g=?}$ από parmenides51
$\displaystyle{(f\circ g)(x)=4-lnx,f(x)=ln(x-2),g=?}$ από parmenides51
$\displaystyle{(f\circ g)(x)=4-lnx,g(x)=e^x+2,f=?}$ από parmenides51
$\displaystyle{(f\circ g)(x)=4-lnx,g(x)=ln(x-2),f=?}$ από parmenides51
$\displaystyle{f(x)=2x^2-1 , x\in[-1,1],g(x)=4x^3-3x , x\in[-1,1],f \circ g=? , g\circ f=?}$ από Στράτη Αντωνέα
$\displaystyle{f(f(x))=x^{2011}}$ από Σπύρο Καπελλίδη

Ερωτήσεις για 1-1 και αντίστροφη
αντίστροφη συνάρτηση από ioakim
ερώτηση στις 1-1 από gurgagr
απορία σε συνάρτηση 1 - 1 από michael
απορία σε άσκηση συναρτήσεων από mixalis_i
είναι Σ ή Λ η παρακάτω πρόταση από Κώστα Τηλέγραφο
ερωτήσεις μαθητών από Κώστα Τηλέγραφο
συνάρτηση από το (α,β) στο R από Γιώργο Απόκη
ερώτηση σωστό λάθος από pito
ερώτηση από Eukleidis
δίκλαδη συνάρτηση 1 - 1 από mixalis_i
μονοτονία και αντίστροφη συνάρτηση από Χρήστο Κανάβη (pana1333)
απορία στα σημεία τομής f και αντίστροφης από Sifis
αντίστροφη συνάρτηση από Γιάννη Στάμου (propaid)
2 απορίες από FERMA
αγγελία από Νίκο Αλεξανδρόπουλο (ενελεκτική μη γραμμική)
ερώτηση στην αντίστροφη από Αγησίλαος

Δεν υπάρχει 1-1 συνάρτηση
$\displaystyle{f(x^2)-f^2(x)\geq \frac{1}{4}}$ από Φωτεινή Καλδή
$\displaystyle{f(f(x))=-x^3}$ από Iason Pap.
$\displaystyle{f(2x)f(4x)f(6x)=2009}$ από math98
$\displaystyle{f(f(x)) =-x,f(f(n)) =-n}$ από Λευτέρη Πρωτοπαπά
$\displaystyle{3{f^3}\left( {{x^5} - {x^4} + {x^3}} \right) - {f^2}\left( {{x^5} - {x^4} + {x^3}} \right) \ge {f^4}\left( x \right) + 4}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f\left( {a \eta \mu x} \right) + f\left( {a \sigma \upsilon \nu x} \right) = {a^2},a \neq 0}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{3f^3(x^5-x^4+x^3)-f^2(x^5-x^4+x^3)\geq f^4(x)+4}$ από Σπύρο Καπελλίδη
$\displaystyle{af(xy)+bf(xz) \geq f(x)f(yz)+c^2,a+b=2c>0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(f(x))=1}$ από pito (κι εδώ)
$\displaystyle{f(x^2+ax-a) \geq f^2\left(\frac {1}{x}\right)-f\left(\frac {1}{x}\right)+1, a>1,χ<0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)=ax^2+bx+c,x\in R-Q,a \neq 0}$ από Σπύρο Καπελλίδη
$\displaystyle{g(x)=ax^2+bx+c, x\in Q,a \neq 0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x) + f(\sqrt x ) + f({x^2}) = 2010,x>0}$ από nonlinear
$\displaystye{e^{f(x)}+2011f(x)=x^4-15}}$ από parmenides51
$\displaystyle{f^{2}(x)\leq f(x)f(10-x)}$ από Γιώργος Κ77
$\displaystyle{2f(x+1)+f(2-x)=2x+4}$ από Γιώργος Κ77
$\displaystyle{(a^{3}-b^{3})f(b)>a^{3}(f(a)-f(b)), a {\neq}b}$ από socrates

Συναρτησιακή εξίσωση - εύρεση 1-1 συνάρτησης
$\displaystyle{f(ax+bf(x))=x,a+b=1}$ από swsto
$\displaystyle{f(x)f\left( {f(x) + \frac{1}{x}} \right) = \frac{1}{2}}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{f(f(x)+y)=f(x)+f(y)}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x+f(y))=f(x+y)+1}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(2x+f(y))=x+y +f(f(x))}$ από Μπάμπη Στεργίου
$\displaystyle{f(x) + f\left( {\frac{{x + f(x)}}{2}} \right) = 2}$ από Γιώργο Τσικαλουδάκη
$\displaystyle{f(x^2f(y))=xyf(f(x))}$ από Μπάμπη Στεργίου
$\displaystyle{f\left( {x + f\left( {y + f\left( z \right)} \right)} \right) = f\left( {x + y + z+1} \right) + 1}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f\circ f=g , g\circ g=f}$ από Σπύρο Καπελλίδη και parmenides51
$\displaystyle{f(f^2(x)+f(y))=xf(x) + y}$ από Μπάμπη Στεργίου
$\displaystyle{f(xf(y))=f(x)f(y)}$ από Σπύρο Καπελλίδη
$\displaystyle{f^2(sinx)-3f(x)+2=0}$ από socrates (εδώ)
$\displaystyle{f(1-x)=1-f(f(x))}$ από socrates
$\displaystyle{f(f(f(x)))=f(x)}$ από maths-!!!

Συναρτησιακή εξίσωση με ερωτήματα με 1-1
$\displaystyle{f(f(x)+f(y))=x+f(y)+2010}$ από Φώτη Χ. Κουτσουμπίδη
$\displaystyle{f\left(\frac{k-m+2f(k)+f(m)}{3}\right)=k+3m}$ από Κωνσταντίνα Κυριακοπούλου
$\displaystyle{f(f(x)) + x = 0}$ από Kagias
$\displaystyle{g(f(x)) = x^3}$ από Μπάμπη Στεργίου
$\displaystyle{f(f(x))=f(x)-x}$ από Γρηγόρη Κωστάκο
$\displaystyle{f(f(x))+f(x)=x}$ από raras
$\displaystyle{f(g(x))=g(f(x))=-x}$ από Μπάμπη Στεργίου
$\displaystyle{ f(x )-f(y)=f\left(\frac{x}{y} \right) }$ από panathas13
$\displaystyle{f(x+y)=f(x+a)f(y-a),f(x) \neq 1}$ από Σπύρο Καπελλίδη
$\displaystyle{f(f(x))=2x+1}$ από Plutarch
$\displaystyle{f(g(x))=2x+1}$ από Plutarch
$\displaystyle{f( x ) = \frac{x}{{1 + \left| x \right|}}}$ από Μάκη Χατζόπουλο και Σωτήρη Λουρίδα
$\displaystyle{f(x) f(1-x)= f(ax+b)}$ από Μπάμπη Στεργίου
$\displaystyle{f(x+y)=f(x) f(y)}$ από nassou13
$\displaystyle{f(xy)=f(x)f(y),g(x)=\frac {f(x)}{x}}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)=\frac{4^{x}}{4^{x}+2}}$ από KARKAR
$\displaystyle{{f^3}( x ) + f( x ) = - g( x )}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(f^2(x)+f(y))=xf(x) + y}$ από Μπάμπη Στεργίου
$\displaystyle{f(x)f(3-x)=f(\lambda x-\kappa )}$ από Γιώργος Κ77
$\displaystyle{f(f(x))=xf(x),x>0,f(x)>0}$ από akis15
$\displaystyle{f(xy)=f(x)+f(y),x,y>0}$ από maths-!!!

1-1 συνάρτηση
$\displaystyle{f(x)=\left\{\begin{matrix} x^2+2ax-1 &, x\leq 0\\ ax-1&, x>0 \end{matrix}\right}}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x) = x^2 -4x + 3, x\in(2, +\infty)}$ από ioakim
1-1 από Βασίλη Μαυροφρύδη (mathxl) (σε μοναδικό διάστημα)
$\displaystyle{f(x)=\ln\left ( - x + \sqrt {1 + x^2 } \right)}$ από Στράτο Παπαδόπουλο
$\displaystyle{f(x)=x^2 -2x - 8 , x\in(-\infty,1)}$ από ioakim
$\displaystyle{ f\left(x + \frac{1}{x}\right) = x^2 - 3x + 5}$ από Αντώνη Σπυριδάκη
$\displaystyle{f(x+y)=(f(x)-1)(f(y)-1)+1,f(x)>1,f(0)=2}$ από coheNakatos
$\displaystyle{F\left(x \right)=f^{3}\left(x \right)+2f\left(x \right)-3, f}$ 1-1 από panathas13
νδο $\displaystyle{\exists x_1 ,x_2 \in [0,2]:2f(x_1 ) - f(x_2 ) < 1}$ εαν $\displaystyle{f(0) + f(2) = 2,f}$ 1-1 από Χρήστο Καρδάση
$\displaystyle{f(a^x)+f(b^{-x})=0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)=ax^2+bx+c,x\in R-Q,a \neq 0}$ από Σπύρο Καπελλίδη
$\displaystyle{g(x)=ax^2+bx+c, x\in Q,a \neq 0}$ από Σπύρο Καπελλίδη
$\displaystyle f(x)=\begin{cases} & \text 2x+6, x\leq 2 \\ & \text x^{2}+1, x>2 \end{cases}$ από Κώστα Καπένη (kostas136)
$\displaystyle{f(x) = \left\{ {\begin{array}{*{20}{c}} {x + 2}&{x > 0}\\ {x + 1}&{x < 0} \end{array}} \right}$ από nonlinear
$\displaystyle{\left| {f(\alpha ) - f(\beta )} \right| \ge \left| {\alpha - \beta } \right|}}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{f(x)=6^x-2\cdot 3^x-9\cdot 2^x+19}$ από Σπύρο Καπελλίδη
$\displaystyle{fog\uparrow, gof\downarrow}$ από Κώστα Σερίφη
$\displaystyle{f(x) = 3x-1+| 2x+1|,g(x) =\frac{1}{5}\left( 3x+5-|2x+5|\right)}$ από socrates
$\displaystyle{\left( {f \circ g} \right)\left( x \right) = \frac{{\sigma \upsilon \nu x - 1}}{{\sigma \upsilon \nu x + 2}}}$ από Βασίλη Μαυροφρύδη (mathxl)
νδο $\displaystyle{\exists x, y \in R, x \ne y:|f (x) - f (y)| \ne 1}$ από socrates
$\displaystyle{f\left( x+y \right)=f\left( x \right)\cdot f\left( y \right),\exists a\in R: f(a)=1,f(x)\ne 0}$ από ghan
περιττή και αντιστρέψιμη από gian7 (η αντίστροφη περιττής είναι περιττή)

Σύνολο τιμών σε συναρτησιακή
$\displaystyle{f^3(x) + f(x) + 2 = x}$ από Kagias
$\displaystyle{g(f(x)) = x^3}$ από Μπάμπη Στεργίου
$\displaystyle{f(f(x))+f(x)=x}$ από raras
$\displaystyle{f(f(x))=4-x}$ από harinho7
$\displaystyle{f(f(x))=2x+1}$ από Plutarch
$\displaystyle{f(g(x))=2x+1}$ από Plutarch
$\displaystyle{f(x) f(1-x)= f(ax+b)}$ από Μπάμπη Στεργίου
$\displaystyle{{{f}^{3}}(x)+f(x)=x}$ από Κώστα Τηλέγραφο
$\displaystyle{f^3(x)+f(x)+x=0}$ από Σπύρο Καπελλίδη
$\displaystyle{f^3(x)+f(x)+1=x}$ από Φωτεινή Καλδή
$\displaystyle{f(xy)=f(x)f(y) ,g(x)=\frac {f(x)}{x}}$ από Σπύρο Καπελλίδη
$\displaystyle f(x)=\frac{4^{x}}{4^{x}+2}$ από KARKAR
$\displaystyle{g^3(x)+g(x)=2e^x+x}$ από g.liolios
$\displaystyle{f^3(x)+f(x)=\frac{a}{\sqrt{x^2+1}},a>0 }$ από Αντώνη Νασιούλα
$\displaystyle{f(f(x))=(f(x)+1)(x+1)}$ από socrates

Αντίστροφη συνάρτηση
απάντηση Α. Πετράκη στα όσα γράφτηκαν στο τεύχος 69 του Ευκλ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{{\log _{\frac{1}{{16}}}}\left( x \right) = {\left( {\frac{1}{{16}}} \right)^x}}$ από papel
$\displaystyle{f(x) =\sqrt{3-\sqrt{4-x}}}}$ από ioakim
$\displaystyle{{\log _{\frac{1}{{100}}}}\left( x \right) = {\left( {\frac{1}{{100}}} \right)^x}}$ από Σεραφείμ Τσιπέλη
$\displaystyle{f(x) = \sqrt {|x - 2| - |x| + 2} }$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x)=\ln\left ( - x + \sqrt {1 + x^2 } \right)}$ από Στράτο Παπαδόπουλο
$\displaystyle{f(x)=x^2 -2x - 8 , x\in(-\infty,1)}$ από ioakim
$\displaystyle{f^3 (x) + f(x) = 2e^x}$ από hsiodos
$\displaystyle{f(f(x))=4x+9}$ από cospash
$\displaystyle{ f\left(x^3+3x^2+3x \right)\leq x\leq f^{3}\left(x \right)+3f^{2}\left(x \right)+3f\left(x \right)}$ από Σπύρο Ορφανάκη
$\displaystyle{f(x) = \ln \left( {\sqrt {1 + x^2 } - x} \right)}$ από Στράτο Παπαδόπουλο (σημείο τομής γν. φθίνουσας με αντίστροφη)
$\displaystyle{f\left( x \right) e^{f\left( x \right)} = x}$ από Μάκη Χατζόπουλο
$\displaystyle{(f \circ f)_{(x)} = x ,f(1992) = 1992,f(2010) = 2010}$ από Kercyn
$\displaystyle{f(f(f(x)))=2x-7}$ από tsolis
$\displaystyle{f(x)=-x^{2},(gof)(x)=\sqrt{1+x^{2}},g=?}$ από christodoulou
$\displaystyle{f^{-1}\bigl({\alpha\,x^5-\beta\,x^3}\bigr)\leq{x}\leq{f^{-1}\bigl({\alpha\,x^4+3x-4\beta+6}\bigr)}, f\left[1,2\right]=\left[-\frac{3}{2},24\right],f \uparrow}$ από Γρηγόρη Κωστάκο
$\displaystyle{f^2(x) - 2f(x)=e^{2x} -1,f(x)>1}$ από Vkalf
$\displaystyle{g\left(x \right)=af\left(x^{3}-1 \right)+\beta,f}$ 1-1 από Χρήστο Κανάβη (pana1333)
$\displaystyle{f(x) = \left\{ {\begin{array}{*{20}{c}} {x + 2}&{x > 0}\\ {x + 1}&{x < 0} \end{array}} \right}$ από nonlinear
$\displaystyle{g(x)=2f(x)+5,f}$ 1-1 από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x)+f^{-1}(x)=2x}$ από Νίκο Αποστολάκη (όχι λυκειακό)
$\displaystyle{\left| {f(\alpha ) - f(\beta )} \right| \ge \left| {\alpha - \beta } \right|}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{{{f}^{3}}(x)+f(x)=x}$ από Κώστα Τηλέγραφο
$\displaystyle{f(x)=-x+\sqrt{1+x^2}}$ από dennys
$\displaystyle{f^{-1}(x)+f(x)=x}$ από gurgagr
$\displaystyle{f(x)=e^{x}(1-x)}$ από KARKAR (σημείο τομής γν. φθίνουσας με αντίστροφη)
$\displaystyle{f^3(x)+f(x)+1=x}$ από Φωτεινή Καλδή
εύρεση της f ^ {-1} (x) από stuart clark (τύπος αντίστροφης τριτοβάθμιας)
$\displaystyle{f^3(x)+f^2(x)= x+2}$ από Κώστα Μπουμπουλή
$\displaystyle{f(x)=x^{5}+x-1}$ από Δημήτρη Ιωάννου
$\displaystyle{f(x) = 3x-1+| 2x+1|,g(x) =\frac{1}{5}\left( 3x+5-|2x+5|\right)}$ από socrates
$\displaystyle{f(x)=(x+1)^5}$ από Geo13bal
$\displaystyle{f(x)=\left\{\begin{matrix} x^2-2x+3& ,x\in(-\infty ,1] & \\ 3-x & ,x\in (1,+\infty) & \end{matrix}\right}}$ από Παναγιώτη Γκριμπαβιώτη
$\displaystyle f(x)=\frac{1}{3}ln\left(x+\sqrt{x^2+1} \right)$ από KARKAR
$\displaystyle{f(x)=-x+ln(-x)}$ από dennys (σημείο τομής γν. φθίνουσας με αντίστροφη)
$\mathrm{f^{-1}(x)=\dfrac{1}{f(x)}}$ από Πέτρο Χρονόπουλο (Μαθηματικός) (ΕΜΕ 2008, 24)

Δεν υπάρχει μονότονη συνάρτηση
$\displaystyle{f\left(f\left(x \right) \right)=x^{2}-x+1,g\left(x \right)+xf\left(x \right)-x^{2}=1}$ από Παύλο Διαμαντή
$\displaystyle{f^2(x^2)-xf(6x-8) \leq 2-\frac {3x}{2}}$ από Σπύρο Καπελλίδη
$\displaystyle{(f(\eta \mu x))^2-3f(x)+2=0}$ από Σπύρο Καπελλίδη
$\displaystyle{f\left(f\left(x \right) \right)=-2^{x}}$ από Χρήστο Κανάβη (pana1333)
$\displaystyle{f(f(x))=f(x)-x}$ από Σπύρο Καπελλίδη

Μονοτονία συνάρτησης με γνωστό τύπο
$\displaystyle{f(x)=\frac{x^{n}+x^{n-1}+...+x+1}{x^{n+1}+x^{n}+...+x+1}, x>0}$ από Ανδρέα Βαρβεράκη
$\displaystyle{f(x)=\frac{x^2+3}{x+a}}$ από rek2

Μονοτονία συνάρτησης με άγνωστο τύπο
νδο $\displaystyle{f(x) = x}$ αν $\displaystyle{(f \circ f \circ f \circ f \circ f)(x) = x,f\uparrow}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{f:R \rightarrow \left( -1,1\right)}$ γν. μονότονη , $g\left( x\right) =\frac{f\left( x\right) }{1+f^{2}\left( x\right) }$ νδο $\displaystyle{g}$ γν. μονότονη από Νίκο Μαυρογιάννη
$\displaystyle{f(\frac {x^2+y^2}{x+y})>f(\frac {x+y}{2}),x+y \neq 0}$ από Σπύρο Καπελλίδη
$\displaystyle{a< f(x)< x, x \in (a,b)}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x)=\frac{x^2+3}{x+a},f }$ γν.μονότονη στο $\displaystyle{[1,+\infty ),a=?}$ ) από Κώστα Ρεκούμη
νδο $\displaystyle{f}$ γν. μονότονη εαν $\displaystyle{f(xy)=f(x)+f(y), (x-1)(f(x))>0}$ από harinho7
$\displaystyle \left (\frac{1}{2}\right)^{f(x^{2}-x)}- \left (\frac{1}{2}\right)^{f(4-x)}>0$ εαν $\displaystyle{h(x)=e^{-f(x)}-f^{3}(x)+2,h \uparrow}$ από Κώστα Καπένη (kostas136)
νδο $\displaystyle{f(x)>0,f \uparrow}$ εαν $\displaystyle{\frac{h(y)}{f(y)}>\frac{f(x)-f(y)}{g(x)-g(y)}>\frac{h(x)}{f(x)}, l x>y>0, g\uparrow, h<0, h}$ φθίνουσα από socrates
νδο $\displaystyle{f(x)=x }$ εαν $\displaystyle{f\left(\frac{2x+3f(x)}{5}\right)=x,f\uparrow}$ από Χρήστο Ευαγγελίνο

Ερωτήσεις για μονοτονία ακρότατα
μονοτονία από exdx
προβληματισμός στον ορισμό της μονοτονίας από Λευτέρη Πρωτοπαπά
ερώτηση από Νίκο Αποστολάκη
ερώτηση (σωστό - λάθος) από christodoulou
απορία σε συνάρτηση 1 - 1 από michael
ρίζα της f(x)=x από Παναγιώτη Γκριμπαβιώτη
ερωτήσεις σωστό λάθος από pito
Σ - Λ: μονοτονία και ένωση διαστημάτων από Μάκη Χατζόπουλο
σωστό ή λάθος? από Eukleidis
2 απορίες από FERMA

Ακρότατα συνάρτησης με γνωστό τύπο
$\displaystyle f(x)=\frac{x}{x^{2}+9}+\frac{1}{x^{2}-6x+21}+\cos{2\pi x}, x>0$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f\left( {\eta \mu ^3 x \right) f\left( {\sigma \upsilon \nu ^3 x } \right)}$ όταν $\displaystyle{f(\varepsilon \phi (x)) = \eta \mu \left( {2x} \right),x\in \left( { - \frac{\pi }{2},\frac{\pi }{2}} \right)}$ από papel
$f(x)=\sqrt{x^{2}-x+1}+\sqrt{x^{2}-\sqrt{3}x+1}$ από rek2 (+ σύνολο τιμών)
$\displaystyle{f(x) = \frac{{2{x^2} + \sigma \upsilon {\nu ^2}x}}{{{x^2} + 1}}}$ από Χρήστο Καρδάση
$\displaystyle{f(x) = \frac{{(x + \frac{1}{x})^6 - (x^6 + \frac{1}{{x^6 }}) - 2}}{{\left( {x + \frac{1}{x}} \right)^3 + \left( {x^3 + \frac{1}{{x^3 }}} \right)}},x > 0}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x)=sin^{13}x+cos^{14}x}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x)=\sqrt{x^2+ax+b}+\sqrt{x^2+cx+d},a^2-4b<0,c^2-4d<0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)=\sqrt{x^{2}-(a\sqrt{3})x+a^{2}}+\sqrt{x^{2}+a^{2}},a>0}$ από KARKAR
$\displaystyle{f(x) = \frac{1}{{1 + |x|}} + \frac{1}{{1 + |x - a|}},a > 0}$ από Χρήστο Κυριαζή (chris_gatos)
$f(x)= \: \begin{vmatrix}\sqrt{x^{2}-8x+52}-\sqrt{x^{2}-4x+8} \: \end{vmatrix}$ από KARKAR και spyros
$\displaystyle{f(x)=\sigma \upsilon \nu ^{2}x+2^{x+1}\eta \mu x-4^{x}}$ από Δημήτρη Ιωάννου
$\displaystyle{f\left( x \right) = \frac{{{x^2} + x - 2}}{{{x^2} + x + 1}},h\left( x \right) = {x^2} + x + \frac{5}{4}},g\left( x \right) =-1 \ln {h\left( x \right)} - 3}$ από Ηλία Καμπελή
$\displaystyle f(x)=\frac{x^{2}-x+1}{x^2+x+1}$ από KARKAR
$\displaystyle{f(x)=|x-1|+|x-2|+|x-3|+|x-4|}$ από Στράτη Αντωνέα
$\displaystyle{f(x)=\sqrt{x^2+16}+\sqrt{x^2-18x+145}}$ από KARKAR

Ακρότατα συνάρτησης με άγνωστο τύπο
$\displaystyle{e^{ - f(x)} - f(x) + 1 - x^2 = 0}$ από Χρήστο Καρδάση
$\displaystyle{h(x)=f(x)f(2-x)+g(x)g(2-x) }$ εαν $\displaystyle{((f(x))^2+(g(x))^2=1}$ από Φωτεινή Καλδή
$\displaystyle{ f(x)=min\left\{4x+1,x+2,-x+2 \right\}}$ από Χρήστο Στραγάλη (συνάρτηση min)
$\displaystyle{f\left( x \right) = \frac{{{x^2} + x - 2}}{{{x^2} + x + 1}},h\left( x \right) = {x^2} + x + \frac{5}{4}},g\left( x \right) = -\ln {\left( {{x^2} + x + \frac{5}{4}} \right)} - 3}$ από Ηλία Καμπελή
νδο $\displaystyle{g,g+f,g-f}$ γν. αύξουσες εαν $\displaystyle{g(x)<2|f(x)-f(a)|,g(x) \ge 2|f(x_{o})-f(a)|+|f(x)-f(x_{o})|, x_{o} \in (a,x) ,x \in (a,b)}$ από wavelet

Θεωρητικές ασκήσεις σε μονοτονία 1-1
περιοδική συνάρτηση από Αναστάσιο Κοτρώνη
μήκος χορδής από Χρήστο Κυριαζή (chris_gatos)
σύνθεση και μονοτονία από Θωμά Ραϊκόφτσαλη (*)
σύντομη με γνησίως αύξουσα από Νίκο Μαυρογιάννη
άρτια - περιττή από Κωνσταντίνα Κυριακοπούλου
συνέχεια - μήκος χορδής από Χρήστο Καρδάση
συνάρτηση συνεχής και 1-1 από Παύλο Διαμαντή
3Γ- ελάχιστο συνάρτησης από Αντώνη Κυριακόπουλο
γνησίως μονότονη συνάρτηση από Σπύρο Καπελλίδη
μονοτονία σύνθεση από Γιώργο Τσικαλουδάκη
1-1, επί και διαγραψιμότητα από Δημήτρη Σκουτέρη
τοπικό μέγιστο σε δύο σημεία διαστήματος από Χρήστο Κυριαζή (chris_gatos)
μονότονη και περιοδική = σταθερή από Νίκο Ζανταρίδη
περιττή συνάρτηση και ακρότατα από Νίκο Ζανταρίδη
ταυτοτική στους ρητούς; ταυτοτική και στους πραγματικούς από Νίκο Ζανταρίδη
άνω φραγμένη και προσθετική; από Νίκο Ζανταρίδη
διπλή ύπαρξη από Ροδόλφο Μπόρη
τη μια επί, την άλλη 1-1 από socrates
άσκηση - συνέχεια από wavelet

Επίλυση εξίσωσης με γνωστό τύπο
$\displaystyle{{6^x} + {8^x} = {10^x}}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{(x^{2}+x-2)^{3}+x^{2}-2=x^{3}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{4^x+(4x-11)2^x+3x^2-23x+30=0}$ από socrates
$\displaystyle{(x+1)^{17}=x^{17}+1}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displastyle\log _{3}(2^{log_{3}(2^{x}+1)}+1)=log_{2}(3^{x}-1)$ από Χρήστο Στραγάλη
$\displaystyle{6^x + 27^{x-1} = 8^{x}-1}$ από erxmer
$\displaystyle{8x^{3}-4\sqrt[3]{8x+15}-15 = 0}$ από KARKAR
$\displaystyle{(x^{2}+x-2)^{3}=x^{3}-x^{2}+2}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{(x^{5}+x+1)^{5}+x^{5}+2=0}$ από tasosjs
$\displaystyle{\sqrt {{e^{{x^2}}}} + \ln x = {e^x} + \ln 2,x > 0}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{2^{x}+ 3^{x} = 97}$ από Ανδρέα Πούλο
$\dipslaystyle{2\sqrt[3]{2y-1}=y^3+1}$ από Παναγιώτη Γκριμπαβιώτη (PanosG)
$\displaystyle{3x(2+\sqrt{9x^{2}+3})+(4x+2)(\sqrt{1+x+x^{2}}+1)=0}$ από Βασίλη Μαυροφρύδη (mathxl)

Επίλυση εξίσωσης με άγνωστο τύπο
$\displaystyle{f^{-1}(x^2+x) = 3}$ όταν $\displaystyle{f(3)=2}$ από Μπάμπη Στεργίου (κι εδώ)
$\displaystyle{f(3 + f^{-1}(x^2+2x)) = 9,f(f^{-1}(x^2 - 8x) -2)<2}$ όταν $\displaystyle{f(5)=9 ,f(2)=3}$ από polysot
$\displaystyle{f(g(x)+x^{2}-2x)=f(g(x)-1)}$ όταν $\displaystyle{(g\circ f)(x)=x+1}$ από Κώστα Καπένη (kostas136)

Επίλυση ανίσωσης με γνωστό τύπο
$\displaystyle{x^{log 3}+x^{log 4}+x^{log 5}>x^{log6},x>0}$ από angvl (εδώ)
$\displaystyle{e^x}\neq \ln x}$ όταν $\displaystyle{e^x\geq x+1}$ από parmenides51
$\displaystyle{x^{11} + 2x^7 + 3x^5 + 5x^3 + 7x < 18}$ από gian7
$\displaystyle{6^x+8^x+16 \cdot 10^x \geq 40^x+3^{\sqrt{x-2}} \cdot 10^x}$ από socrates
$\displaystyle{1^{x}+2^{x}+6^{x}+12^{x}\geq 4^{x}+8^{x}+9^{x}}$ από socrates

Επίλυση ανίσωσης με άγνωστο τύπο
$\displaystyle{f(3 + f^{-1}(x^2+2x)) = 9,f(f^{-1}(x^2 - 8x) -2)<2}$ όταν $\displaystyle{f(5)=9 ,f(2)=3}$ από polysot
$\displaystyle f(\ln x) g(1)>g(\ln x)f(1)$ όταν $\displaystyle{f,g>0,f\uparrow, g\downarrow }$ από Κώστα Καπένη (kostas136)
$\displaystyle \left (\frac{1}{2}\right)^{f(x^{2}-x)}- \left (\frac{1}{2}\right)^{f(4-x)}>0$ εαν $\displaystyle{h(x)=e^{-f(x)}-f^{3}(x)+2,h \uparrow}$ από Κώστα Καπένη (kostas136)
$\displaystyle{g(f(x^2 )) < 0}$ όταν $\displaystyle{f(0)=-1, g(-1)=0, f,g}$ γν.μονότονες από Σπύρο Καρδαμίτση
$\displaystyle{f\left( {1 - {f^{ - 1}}\left( x \right)} \right) < 3}$ όταν $\displaystyle{f(0)=3,f(1)=2,f}$ γν.μονότονη από Atemlos

Απόδειξη ανισότητας με γνωστό τύπο
$\displaystyle{\sin ( \cos 1)<\cos ( \sin 1)}$ από Δημήτρη Σκουτέρη
$\displaystyle{\sqrt{2}+\sqrt{3}>\pi}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\cos 3x - \cos 2x < x,x \in \left(0,\frac{\pi }{3}\right)}$ από Χρήστο Καρδάση
$\displaystyle{\frac{{5x}}{{\eta \mu x}} > 4 - \sigma \upsilon \nu x,x \in \left( {0,\frac{\pi }{2}} \right)}$ από Βασίλη Μαυροφρύδη (mathxl)

Ύπαρξη ρίζας με μονοτονία
νδο η εξίσωση $\displaystyle{3f(x) + 5g(x) +8f(x)g(x) = 0}$ έχει το πολύ μια ρίζα όταν $\displaystyle{f,g \uparrow, f,g<0}$ από Μπάμπη Στεργίου
νδο η εξίσωση $\displaystyle{ f(x)+g(x)=f(x)g(x)}$ έχει το πολύ μια ρίζα όταν $\displaystyle{f,g \downarrow, f,g>0}$ από Κώστα Καπένη (kostas136)
νδο η εξίσωση $\displaystyle{f(2x-1)=-f(x+2)}$ έχει μοναδική ρίζα όταν $\displaystyle{f(5)=0,f\uparrow}$ από katsaounisgiannis
νδο $\displaystyle{\exists x_0 : f(x_0)>1}$ εαν $\displaystyle{f(f(x)) = \frac{x}{{\sqrt {x^2 + 2} }},f\uparrow}$ από Σπύρο Καπελλίδη (εδώ)
$\displaystyle{3^x+4^x=5^x + x - 2 }$ από Μπάμπη Στεργίου

Συναρτησιακή με χρήση ορίου
$\displaystyle{f(xf(y)) = yf(x),x,y>0,\mathop {\ell im}\limits_{x \to + \infty } f(x) = 0}$ από Ραϊκόφτσαλη Θωμά
$\displaystyle{ f(f(x))=x+4 }$ , υπάρχει το όριο $\displaystyle{\lim_{x\rightarrow \infty}( f(x)-x)}$ από socrates
$\displaystyle{\alpha x<f\left(x \right)\leq \alpha x+1,\alpha \neq 0, f^2\left(x \right)=xf\left(2x+1 \right)+x+1,x>0,}$ από Νίκο Ζανταρίδη
$\displaystyle{f(e^x+y)=f(e^y+x)}$ από Σπύρο Καπελλίδη **
νδο $\displaystyle{f(x)=xf(1), x\ne 0}$ εαν $\displaystyle{f(x+y)=f(x)(1+yf(y))}x\ne 0, y \in (-1,0)\cup(0,1),\lim_{x \rightarrow 0}f(x)\in R}$ από Pla.pa.s
$\displaystyle f(x^3)=f(x^2)+f(x), x>0$ όταν $\displaystyle \lim_{x\rightarrow 1}\frac{f(x)}{x-1}=k$
$\displaystyle{\lim_{y\rightarrow +\infty }f(y)=f(x), \forall x\in R}$ από parmenides51

Ερωτήσεις στα όρια
ερωτήσεις μαθηματικών από solon28
υπολογισμός ορίου από Χρήστο Κυριαζή (chris_gatos) (εδώ)
επισημάνσεις στη θεωρία των ορίων από Στέλιο Μαρίνη
Σ - Λ από Βασίλη Μαυροφρύδη (mathxl)
απορία σε όριο από tsalikdimd
το γνωστό ( ?? ) όριο sinx/x από Linardatos
ένα όριο από Νίκο Μαυρογιάννη
βρες τήν συνάρτηση από nonlinear
απορία σε ερώτηση σωστού λάθους από Γιάννη Στάμου (propaid)
κριτήριο παρεμβολής στο άπειρο από Γιώργο Ασημακόπουλο (εδώ)
υπάρχουν τέτοιες συναρτήσεις h,g; από epameinondas
ερωτήσεις μαθητών από Κώστα Τηλέγραφο
κυκλικές αποδείξεις από Κώστα Αθανασιάδη
όριο σύνθετης από Πέτρο Χρονόπουλο (Μαθηματικός)
αντίστροφα θεωρημάτων από pito
απορίες για το πεδίο ορισμού από Ardid
μια διευκρίνηση από Christiano
που είναι το λάθος; από Χρήστο Κανάβη (pana1333)
όριο στο άπειρο από margk
απροσδιοριστίες από mixalis_i
όρια από Αντώνη Νασιούλα
όριο και συνέχεια σύνθετης από dennys
σωστό - λάθος στα όρια από Κώστα Αθανασιάδη (kost65)
απορία στο κριτήριο παρεμβολής από Γιώργο Απόκη
απορία από pito
απορία σε όρια από Γιώργο Απόκη
2 ερωτήσεις για τα μαθηματικά κατεύθυνσης από Δημήτρη Κατούνη
όριο σύνθετης από orestisgotsis
μια απορία στα όρια από akis15
ερώτηση από miltos

Όρια ασυνήθιστα
νδο $\displaystyle{\nexists \mathop {\lim }\limits_{x \to 1} f(x)}$ εαν $\displaystyle{f(x) = \left\{ {\begin{array}{*{20}c} {a^2 x^2 + 2a\beta x + \alpha \;,\;x < 1} \\ {3^{2010} x^2 - \beta (\beta + 1)\,x\;,\;x \ge 1} \\ \end{array}} \right.\quad ,\alpha,\beta \in Z}$ από Χρήστο Καρδάση
νδο $\displaystyle{ \exists \lim_{x\rightarrow 1}\frac{1}{f\left(x \right)} }$ όταν $\displaystyle{\nexists \lim_{x\rightarrow 1}f\left(x \right) ,\exists \lim_{x\rightarrow 1^{\pm}}f\left(x \right)<\infty}$ από Χρήστο Κανάβη (pana1333)
$\displaystyle{\mathop {\lim }\limits_{x \to x_0 } \frac{{\kappa f(x)}}{{f(x) + \lambda }} =\mathop {\lim }\limits_{x \to x_0 } f(x)=l\in R,f(x)>0, f(x)\neq- \lambda, \lambda=?}$ από xgastone
$\displaystyle{\lim_{x \to 2}\frac{ax^2-(a-1)x+8}{x-2}=b-b^2,a,b\in Z , a,b=?}$ από erxmer
$\displaystyle{\mathop {\lim }\limits_{x \to 1^ + } f\left( {f(x)} \right)=?}$ εαν $\displaystyle{f(x) = \left\{ \begin{matrix} \displaystyle \frac{x^{^2 } - 1}{x^3 - 1} &, x< 1 \\ \displaystyle \frac{1}{x} &, x > 1 \end{array} \right}}$ από Γιώργο Τσικαλουδάκη και Pla.pa.s
$\displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,f(x),\underset{x\to -\infty }{\mathop{\lim }}\,f(x),\underset{x\to 2}{\mathop{\lim }}\,f(x)}$ εαν $\displaystyle{f(x)=\frac{{{\beta }^{\chi }}-{{\alpha }^{\chi }}-{{\gamma }^{\chi }}}{{{\beta }^{\chi }}+{{\gamma }^{\chi }}-{{\alpha }^{\chi }}},\triangle ABC,\hat{A}=\frac{\pi }{2},\hat{B}>\frac{\pi }{4}}$ από Βασίλη Κακαβα
$\displaystyle{\underset{x\to 2}{\mathop{\lim }}\,g(x)}$ εαν $\displaystyle{g(x)=\frac{{{x}^{2}}-2x(\eta \mu \frac{\pi x}{4}+1)+4\eta \mu \frac{\pi x}{4}}{{{\beta }^{\chi }}+{{\gamma }^{\chi }}-{{\alpha }^{\chi }}},\triangle ABC,\hat{A}=\frac{\pi }{2},\hat{B}>\frac{\pi }{4}}$ από Βασίλη Κακαβα

Όρια χωρίς δεδομένα
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \frac{{{f^4}(x)}}{{{x^3}}} + \frac{{{x^9}}}{{{f^4}(x)}}}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{f\left( x \right)}}{x} + \frac{{x^3 }}{{f\left( x \right)}}} \right)}$ από Στάθη Κούτρα

Όριο αντίστροφης
$\displaystyle{\lim_{x\to 0}\frac{\eta\mu x}{f^{-1}(x)}}$ όταν $\displaystyle{f^3(x) + f(x) + 2 = x}$ από Kagias
$\displaystyle\lim_{x\rightarrow+\infty}\frac{f^{-1}(x)}{lnx}$ όταν $\displaystyle{f\left(x \right)=e^{x}+x^{3}-x^{2}+x}$ από christodoulou
$\displaystyle{\mathop {\lim }\limits_{x \to 0} f^{ - 1} (x)}$ όταν $\displaystyle{f ^{3}(x)+ f(x) = e^{x}+ x - 1}$ από Πέτρο Χρονόπουλο (Μαθηματικός)
$\displaystyle{g^{-1}(-5)=?}$ όταν $\displaystyle{\lim_{x\to\ 2}\frac{f^{-1}(x)+3}{x-2}=-2,\ g(x)=\frac{f(x)+3}{f(x)-3}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\lim_{x\to 0}\frac{f^{-1}(x)}{x+f^{-1}(x)}}$ όταν $\displaystyle{f(x)=2x-\eta\mu^2x,x\in(0,2\pi)}$ από Φωτεινή Καλδή
$\displaystyle{\lim_{x\to +\infty}\frac{\eta\mu x}{f^{-1}(x)}}$ όταν $\displaystyle{f^3(x)+f(x)+1=x}$ από Φωτεινή Καλδή
$\displaystyle\lim_{x\rightarrow 1}f^{-1}(x)}$ όταν $\displaystyle{f(x)\geq x, x \in R, f^{-1}(x)\geq lnx +1 ,x>0}$ από Παναγιώτη Γκριμπαβιώτη
$\displaystyle\lim_{x \to \pm \infty } f^{ - 1} (x)$ όταν $\displaystyle{f(x) = e^x + x}$ από Γιώργο Τσικαλουδάκη
$\displaystyle{\mathop {\lim }\limits_{x \to - \infty } \tfrac{{{f^{ - 1}}\left( x \right) - x}}{{x + {f^{ - 1}}\left( x \right)}}}$ όταν $\displaystyle{f\left( x \right) = \tfrac{1}{x} - {x^3} + 1},x>0$ από Eukleidis
$\displaystyle{\underset{x\to 9}{\mathop{\lim }}\,{{f}^{-1}}(x)}$ εαν $\displaystyle{\left( 3,2 \right),\left( 5,9 \right) \in C_f , f}$ γνησίως μονότονη από orestisgotsis

Δίνεται συναρτησιακή, ζητείται όριο
$\displaystyle{\mathop {\ell im}\limits_{x \to {0^ + }} \frac{{f(x)}}{x}}$ όταν $\displaystyle{\left| {f(x) - f(y)} \right| \ge \left| {{2^x} - {2^y}} \right|}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{2f(x) = x + \eta \mu \left( {f(x)} \right)}$ από Χρήστο Καρδάση
$\displaystyle{f^3 (x) + f(x) = 2e^x}$ από hsiodos
$\displaystyle{f^3(x) + f(x) + 2 = x}$ από Kagias
$\displaystyle{\lim_{x \to 0}\frac{f(x)}{x}= \lambda}$ όταν $\displaystyle{f^{2}(x)(f(x)-4x)=x^{2}(6x-7f(x))}$ από georgeman
$\displaystyle{{f^3}(x) + f(x) - 1 = 0}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{\mathop {lim}\limits_{x \to 2} f(x)}$ όταν $\displaystyle{h(x) \le f(x) \le g(x),\mathop {lim}\limits_{x \to 2} h(x) = {\lambda _1}},\mathop {lim}\limits_{x \to 2} g(x) = {\lambda _2},\lambda _1,\lambda _2 > 0}$ από Χρήστο Καρδάση
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left(1 + \frac{{\ln x}}{{f(x)}}\right)^{\frac{{f(x)}}{x}} }$ όταν $\displaystyle{f(x)\ln (f(x)) = e^x}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{\lim _{x\rightarrow 4}\frac{f(x)-\sqrt{g(x)}+\sqrt{5}}{\sqrt{g(x)}-\sqrt{5}}}$ όταν $\displaystyle{(f\circ g)=\sqrt[3]{5}\left|x-3 \right|^{\frac{2}{3}}, g(x)\geq 0}$ από erxmer
$\displaystyle{\lim_{x\rightarrow +\infty}\frac{f(x)}{x^3},\lim_{x\rightarrow +\infty}\frac{f(x)}{x} }$ όταν $\displaystyle{f^3(x)+f(x)=x^3}$ από Χρήστο Τσιφάκη
$\displaystyle{3f(x)=2x+\sin f(x)}$ από Στράτη Αντωνέα (εδώ κι εδώ)
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } f(x),\mathop {\lim }\limits_{x \to \frac{4}{3}} f\left( x \right)}$ όταν $\displaystyle{f^3 (x) + 3f(x) = 3x}$ από Γιώργο Τσικαλουδάκη και Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\lim_{x \to 1}\frac{f^2(x)-9}{x^2-4x+3}}$ όταν $\displaystyle{f(e^{2x})+2f(x^2+1)=x+9}$ από erxmer
$\displaystyle{f^3(x)+f(x)+1=x^2}$ από μαριαννα
$\displaystyle{f^{3}(x)+2f(x)-x=2006}$ από Christiano
$\displaystyle{\lim_{x \rightarrow +\infty} \frac{f(x)}{x^{5}}}$ όταν $\displaystyle{f^{2}(x) \le 4xf(x)-3x^{2}}$ από Christiano
$\displaystyle{\mathop {\lim }\limits_{x \to 1} f(x) = \ell \in \R}$ όταν $\displaystyle{e^{f(x)} + f(x) = \ln x}$ από Σπύρο Καρδαμίτση
$\displaystyle{\lim_{x\to 0}f(x),\lim_{x\to\pm\infty}f(x),\lim_{x\to\pm\infty}\frac{f(x)}{x}}$ όταν $\displaystyle{2f(x)+\eta \mu (f(x))=x}$ από Βασίλη Κακαβα
$\displaystyle{\underset{x\to -\,\infty }{\mathop{\lim }}\,\frac{f(x)}{{{x}^{2}}}}$ όταν $\displaystyle{{{f}^{2}}(x)\le 2xf(x)}$ από ghan
$\displaystyle{\underset{x\to \,-\infty }{\mathop{\lim }}\,f(x),\underset{x\to 0}{\mathop{\lim }}\,\frac{f(x)}{\sin \left| x \right|}}$ όταν $\displaystyle{{f}^{2}}(x)=2xf(x)+1,f(0)=1}$ από ghan

Δίνεται όριο, ζητείται όριο, θεωρητικές
$\displaystyle\mathop{\lim}\limits_{x\rightarrow{+\infty}}{({f(x)})^{x}},\mathop{\lim}\limits_{x\rightarrow{+\infty}}{({g(x)})^{x}}$ όταν $\displaystyle{0<\mathop{\lim}\limits_{x\rightarrow{+\infty}}{f(x)}<1<\mathop{\lim}\limits_{x\rightarrow{+\infty}}{g(x)}=l\in R}$ από Γρηγόρη Κωστάκο
$\displaystyle{\mathop {\ell im}\limits_{x \to 0} f(x) = \mathop {\ell im}\limits_{x \to 0} k(x) = 0}$ όταν $\displaystyle{g(x) = {f^2}(x) + {x^4} + 1,h(x) = {k^2}(x) + \left| x \right| + 1,\mathop {\ell im}\limits_{x \to 0} \left( {g(x) + h(x)} \right) = 2}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{\,\mathop {\lim }\limits_{x \to 0} f(x) ,\mathop {\lim }\limits_{x \to 0} g(x) }$ όταν $\displaystyle{f(x) \ge 0\,\,\,\,\kappa \alpha \iota \,\,\,\,g(x) \ge 0,\mathop {\lim }\limits_{x \to 0} [f(x) + g(x)] = 0\,}$ από hsiodos
$\displaystyle{\lim_{x\rightarrow 0}f(x),\lim_{x\rightarrow 0}g(x)}$ όταν $\displaystyle{ f^2(x) \leq f^2(x)+g^2(x) \leq sin^2x}$ από harinho7
$\displaystyle{\mathop {\lim }\limits_{x \to \alpha } \left( {f\left( x \right) + g\left( x \right)} \right) = \mathop {\lim }\limits_{x \to \alpha } \left( {f\left( x \right) g\left( x \right)} \right) = 0}$ από Μάκη Χατζόπουλο
$\displaystyle{\lim_{x\rightarrow x_{o}}f(x),\lim_{x\rightarrow x_{o}}g(x)}$ όταν $\displaystyle{f(x),g(x)\geq 1,\lim_{x\rightarrow x_{o}}[f^{3}(x)+g^{3}(x)]=2}$ από margk
$\displaystyle{(\mathop {\lim }\limits_{x \to x_o } f(x) = \mathop {\lim }\limits_{x \to x_o } g(x) = 0) \Leftrightarrow \mathop {\lim }\limits_{x \to x_o } (f^2 (x) + g^2 (x)) = 0}$ από Σπύρο Καρδαμίτση
$\displaystyle{\mathop {\lim }\limits_{x \to x_0 } \left[ {\max \left\{ {f(x),g(x)} \right\}} \right] = \max \left\{ {l,m} \right\}, \mathop {\lim }\limits_{x \to x_0 } \left[ {\min \left\{ {f(x),g(x)} \right\}} \right] = \min \left\{ {l,m} \right\}}$ όταν $\displaystyle{ \mathop {\lim }\limits_{x \to x_0 } f(x) = l \in R , \mathop {\lim }\limits_{x \to x_0 } g(x) = m \in R}$ από Νίκο Ζανταρίδη
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{f(x)}},\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{g(x)}}}$ όταν $\displaystyle{x^2 f(x) + x^2 g(x) - f^2 (x)g^2 (x) = 0,x>0}$ από Σπύρο Καρδαμίτση
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } f\left( x \right),\;\mathop {\lim }\limits_{x \to + \infty } g\left( x \right)} }$ όταν $\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left( {f^3 (x) - g^3 (x)} \right) =\mathop {\lim }\limits_{x \to + \infty } \left( {f(x) g(x)} \right) = 0} }$ από Σωτήρη Λουρίδα

Δίνεται όριο, ζητείται όριο
$\displaystyle\mathop {\lim }\limits_{x \to 0} \frac{{{e^{f\left( x \right)}} - 2x - 1}}{x}$ όταν $\displaystyle\mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - 2x}}{x} = 4$ από Χρήστο Κυριαζή (chris_gatos)(εδώ)
$\displaystyle{\mathop {\lim }\limits_{x \to 0} f\left( x \right) = + \infty}$ όταν $\displaystyle{\mathop {\lim }\limits_{x \to 0} \left[ {2f\left( x \right) - f\left( { - x} \right)} \right] = + \infty}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle\lim_{x\to2}f(x)$ όταν $\displaystyle\lim_{x\to2}(f(x)+3f(4-x))=4$ από Αναστάσιο Κοτρώνη
$\displaystyle{\lim_{x\rightarrow +\infty }\left[\frac{1}{x^{2}} f\left(\frac{2}{x} \right) \right] }$ όταν $\displaystyle { \lim_{x\rightarrow 0}\left[x^{2} f\left(x \right) \right]=1 }$ από panathas13
$\displaystyle \lim_{x \rightarrow 2}\frac{f(x)}{sin(\pi x)}$ όταν $\displaystyle \lim_{x \rightarrow 2}\frac{f(x)}{x-2}=3$ από Κώστα Καπένη (kostas136)
$\displaystyle{\mathop {\lim }\limits_{x \to 2} f(x),\mathop {\lim }\limits_{x \to 2} g(x)}$ όταν $\displaystyle{\mathop {\lim }\limits_{x \to 2} \left[ {xf(x) - 2g(x)} \right] = 3,\mathop {\lim }\limits_{x \to 2} \left[ {f(x) - \sqrt {1 + 4x} g(x)} \right] = 5}$ από ZITAVITA
$\displaystyle\lim_{x\to 0}f(x)$ όταν $\displaystyle\lim_{x\to 0}\left(f(x)+ \frac {1}{f(x)} \right)=2$ από Σπύρο Καπελλίδη
$\displaystyle{\mathop {\lim }\limits_{x \to 1} f\left( x \right) }$ όταν $\displaystyle{\mathop {\lim }\limits_{x \to 1} \left[ {e^{f\left( x \right)} - f\left( x \right)} \right] = 1}$ από από Στάθη Κούτρα
$\displaystyle{\mathop {\lim }\limits_{x \to 0} f(x)}$ όταν $\displaystyle{f(\alpha - x) = f(x) + x,\mathop {\lim }\limits_{x \to \alpha } (2f(x) + 2x - \alpha ) = 1}$ από Σπύρο Καρδαμίτση
$\displaystyle{\underset{x\to 1}{\mathop{\lim }}\,\frac{{{f}^{2}}(x)-f(x)-2}{\sqrt{{{f}^{2}}(x)+3}-2x}}$ όταν $\displaystyle{\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)+x}{x-1}=2}$ από Βασίλη Κακαβα
$\displaystyle{\underset{x\to 1}{\mathop{\lim }}\,\frac{f(x)-2{{x}^{2}}}{{{x}^{3}}-1}}$ όταν $\displaystyle{\underset{x\to 1}{\mathop{\lim }}\,\frac{{{f}^{2}}(x)+f(x)-6}{x-1}=5}$ από Βασίλη Κακαβα
$\displaystyle\lim_{x\rightarrow 4}\frac{f(x)-1}{x-4}$ όταν $\displaystyle{f(x)=f(x+3), \lim_{x\rightarrow 1}\frac{f(x)-1}{x-1}=2}$ από margk
$\displaystyle{\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{{{(\sqrt{1+{{f}^{2}}(x)}+2f(x))}^{10}}-{{(\sqrt{1+{{f}^{2}}(x)}-3f(x))}^{10}}}{f(x)}}$ όταν $\displaystyle{\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x)=0}$ από Βασίλη Κακαβα
$\underset{x\to \infty }{\mathop{\lim }}\,\frac{f(100x)}{f(x)}$ όταν $\underset{x\to \infty }{\mathop{\lim }}\,\frac{f(2x)}{f(x)}=1. f\nearrow$ από ghan
$\mathop {\lim }\limits_{x \to - \infty } f(x)$ όταν $\mathop {\lim }\limits_{x \to - \infty } \left( {e^{f(x)} + f(x)} \right) = - \infty$ από Γιώργο Τσικαλουδάκη
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \frac{{\ln \left( {f\left( x \right)} \right)}}{{\ln x}}}$ όταν $\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = l >0}$ από Νίκο Ζανταρίδη
$\displaystyle{ \lim_{x\rightarrow 3}f(x)}$ όταν $\displaystyle \lim_{x\rightarrow 3}[f(x)+2f(6-x)]=3$ από Κώστα Καπένη (kostas136)

Υπολογισμός παραμέτρων σε ισότητα ανισότητα χρησιμοποιώντας όρια
$\displaystyle{\kappa \alpha ^x + \lambda \beta ^x + \mu \gamma ^x = 0}$ από Χρήστο Καρδάση
$\displaystyle{a \eta \mu (2009x) + b \eta \mu (2010x) \le c \eta \mu (2011x)}$ από Χρήστο Λαζαρίδη
$\displaystyle{\lim_{x\rightarrow 0}\frac{sin^{2010}x-sinx^{2010}}{x^{^{n}}}=l\in R^*}$ από Νίκο Αποστολάκη
$\displaystyle{\lim_{x\rightarrow 0}\frac{a\left\vert \varepsilon \varphi x\right\vert +\sqrt{x^{2}+x^{4}}}{\sqrt{x^{2}+x+1}-1}\in R,a\in R ?}$ από erxmer
$\displaystyle{\eta \mu (\alpha x)\leq \eta \mu (\beta x)+\eta \mu (\gamma x)}$ από pito
$\displaystyle{\lim_{x \rightarrow +\infty}\left(x^{\frac{x+1}{x}}+ax \right)=0,a\in R ?}$ από STOPJOHN
$\displaystyle{a{{e}^{x}}+\beta {{e}^{-x}}\ge 2}$ από Βασίλη Κακαβα
$\displaystyle{cos ax+cos bx-cos 2011x\leq 1}$ από Γιώργος Κ77

Όρια σε πραγματικό
$\displaystyle{\lim_{x\rightarrow 1}\frac{x-1-\sqrt{x^2-3x+2}}{\sqrt{x^2-3x+2}-\sqrt{x^2-4x+3}}}$ από Στέλιο Μαρίνη
$\displaystyle \lim_{x\to1}\frac{x^{3n-2}\sqrt{x}-1}{1-x^{2n}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[k]{x} - 1}}{{x - 1}} k \in {N^*},\mathop {\lim }\limits_{x \to 1} \frac{{(1 - \sqrt x )(1 - \sqrt[3]{x})...(1 - \sqrt[{100}]{x})}}{{{{(1 - x)}^{99}}}},\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\sqrt[{10}]{{\eta \mu x}} - 1}}{{\sigma \upsilon {\nu ^2}x}}}$ από Χρήστο Λαζαρίδη
$\displaystyle\lim_{x\to 1}\frac{x^{n+1}-(n+1)x+n}{(x-1)^2},n\in N^{\star}$ από Χρήστο Τσιφάκη
$\displaystyle\mathop{\lim}\limits_{x\rightarrow0^{+}}\frac{\ln{x}}{x}$ από tsolis
$\displaystyle\mathop{\lim}\limits_{x\rightarrow0^{+}}\left({x^5\,\sin\tfrac{10}{x}}\right)$ από tsolis
$\displaystyle{\lim_{x\rightarrow 0}\frac{\sqrt[3]{x+8}-2}{x}}$ από ioakim
$\displaystyle{\lim_{x\rightarrow 1}\frac{x^{2}-\sqrt{x}}{\sqrt{x}-1}}$ από ioakim
$\displaystyle{\mathop {\lim}\limits_{x \to - 5} \;\;\frac{{\sqrt {x ^2 + 10x + 25} }}{{x + 5}}}$ από ioakim
$\displaystyle{\lim_{x\rightarrow 0}\frac{\eta \mu x(e^x-1)}{1-\sigma \upsilon \nu x}}$ από vzf
$\displaystyle{\lim_{x\rightarrow 0}\frac{\eta \mu(x^2)}{(1-\sigma \upsilon \nu x)^{2010}}}$ από vzf
$\displaystyle{\lim_{x\rightarrow 0}\left(\frac{1+e^{4x}}{1+\sigma \upsilon \nu x} \right)^{\sigma \varphi x}}$ από vzf
$\displaystyle{\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \left[ {\left( {\varepsilon \varphi x - 1} \right)\left( {1 - \varepsilon \varphi \frac{x}{2}} \right)} \right]}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\mathop {\lim }\limits_{x \to 0} \frac{{\eta {\mu ^2}x - {x^2}}}{{{x ^2}\eta {\mu ^2}x }} }$ από tsalikdimd
$\displaystyle{\lim_{x\to 0}(\displaystyle\frac{x^{2}}{sinx}sin\frac{x-1}{x})}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\lim_{x\to 0}(\displaystyle\frac{x^{2}}{tanx}cos\frac{2}{x})}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\mathop{\lim}\limits_{x\rightarrow{e}}{\ln({\ln({\ln{x}})})}}$ από VASILISt
$\displaystyle\lim_{x\rightarrow 0}\frac{x\sin \frac{1}{x}}{x-\sin x}$ από Γιώργο Ασημακόπουλο
$\displaystyle{\lim_{x\rightarrow 1}\frac{(1-\sqrt{x})(1-\sqrt[3]{x})(1-\sqrt[4]{x})...(1-\sqrt[\nu ]{x})}{(1-x)^{\nu -1}}, \nu \geq 2}$ από Παντελή Βενάρδο (smarpant)
$\displaystyle{\lim_{x\rightarrow -2}\frac{\sqrt{x^2+2x}}{x+2}}$ από mixalis_i
$\displaystyle{\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x}}$ όταν το $\displaystyle{x}$ εκφράζει μοίρες από Σωτήρη Λουρίδα (κι εδώ) (όριο σε μοίρες)
$\displaystyle{\lim_{x\to2} \frac{2^x+2^{3-x}-6}{\sqrt{2^{-x}}-2^{1-x}}}$ από irakleios
$\displaystyle{\lim_{x\to a}\frac{\sqrt{x}-\sqrt{a}+\sqrt{x-a}}{\sqrt{x^2-a^2}}}$ από irakleios
$\displaystyle{\mathop {\lim }\limits_{x \to 3 }ln(-x^2+7x-10)+3\sqrt{cos(\pi\sqrt{x^2+7})-1}-ln2}$ από Παναγιώτη Γκριμπαβιώτη
$\displaystyle\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\sigma \upsilon {\nu ^a}x}}{{{{(1 - \eta \mu x)}^b}}},a ,b > 0$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{x + \sqrt[4]{x}}}}}{{\sqrt[4]{{x + \sqrt[3]{x}}}}}}$ από Σπύρο Καρδαμίτση
$\displaystyle{\mathop {\lim }\limits_{x \to 2} \left( {\frac{{\sqrt {1 - \sigma \upsilon \nu \left( {2\left( {x - 2} \right)} \right)} }}{{x - 2}}} \right)}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle {\lim_{x \rightarrow 0}(\frac{2}{x}-ln(1+e^{\frac{2}{x}}))}$ από Christiano
$\displaystyle{\lim_{x\rightarrow 0} \frac{sin^{2}(x)sin(\frac{\pi}{x})}{x}}$ από Christiano
$\displaystyle{\lim_{x\rightarrow 0}\frac{e^x}{lnx}}$ από parmenides51
$\displaystyle{\lim_{x\rightarrow 0}\frac{lnx^2}{x}$ από parmenides51
$\displaystyle\lim_{x \to 7}\frac{\sqrt{x+2}-\sqrt[3]{x+20}}{\sqrt[4]{x+9}-2}$ από irakleios
$\displaystyle{\mathop{\lim}\limits_{x\rightarrow\alpha}{\frac{\sqrt{x^2-3\alpha{x}+3\alpha^2}-\alpha}{|{x}|-\alpha}}\,, \ \alpha\in R}$ από kostakos ale
$\displaystyle{\lim_{x\to 0}\frac{x+\sin x}{x^3+x^2}}}$ από Ωmega Man
$\displaystyle{\lim_{x\to 0}\frac{e^x-2}{\sin 7x}}$ από Ωmega Man
$\displaystyle{\underset{x\to 0}{\mathop{\lim }}\,\frac{1+2{{\cos }^{3}}x-3\sqrt{\cos 2x}}{{{\sin }^{4}}x}}$ από ghan
$\displaystyle{\mathop {\lim }\limits_{x \to 0} \frac{{\sin (2\sin (2\sin x))}}{{\tan (2\tan (2\tan x))}}}$ από mathxl
$\displaystyle\underset{x\to 1}{\mathop{\lim }}\,\left( \left( 1-x \right)\tan \frac{\pi x}{2} \right)$ από ghan
$\displaystyle{\underset{x\to 0}{\mathop{\lim }}\,\left\{ {{x}^{-2}}\left( \sqrt{\cos \alpha x}-\sqrt{\cos \beta x} \right) \right\},\alpha ,\beta ,\alpha -\beta \ne 0}$ από ghan
$\displaystyle{\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{1+x\sin x}-\cos x}{{{\displaystyle\sin }^{2}}\frac{x}{2}}}$ από ghan
$\displaystyle{\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin ({{x}^{30}}+2x)}{5x+{{x}^{100}}}}$ από ghan
$\displaystyle{ \lim_{x \to \ +\infty }\left(\eta \mu {\sqrt{x+1}}-\eta \mu\sqrt{x} \right)}$ από irakleios
$\displaystyle{\mathop {\lim }\limits_{x \to 1} \frac{{(1 - x)(1 - {x^2}) \ldots (1 - {x^{2n}})}}{{{{[(1 - x)(1 - {x^2})(1 - {x^3}) \ldots (1 - {x^n})]}^2}}},n \in {N^ * }}$ από mathxl

Όρια με τον περιορισμό χωρίς de l' Hospital
$\displaystyle{\lim_{x\rightarrow \frac{\pi }{2}} \frac{1-\eta \mu x}{\sqrt{1+\sigma \upsilon \nu 2x}}}$ από Κώστα Καπένη
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{{2009x + 20}}{{2009x}}} \right)^{ - \frac{x}{5}}}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle\lim_{x\rightarrow +\infty}\displaystyle\frac{x 2^{x+1}-3 3^{x}}{4 5^{x}-x 2^{x}}$ από Σπύρο Ορφανάκη
$\displaystyle{\lim_{x\rightarrow 0} \frac{1-\sqrt{cos(x)}}{x^2}}$ από ioakim
$\displaystyle\mathop{\lim}\limits_{x\rightarrow+\infty}{\frac{\ln{\frac{2+\eta\mu{x}}{6+\sigma\upsilon\nu{x}}}}{x}}$ από Γρηγόρη Κωστάκο
$\displaystyle{\lim_{x\rightarrow 0} \frac { 1 - \sqrt { \sigma \upsilon \nu x}}{x^2}}$ από ioakim
$\displaystyle{\lim_{x\rightarrow 0}\frac{\frac{sinx}{x}-1}{x}}$ από Κική
$\displaystyle\mathop {\lim }\limits_{x \to 0} \frac{{1 - \sigma \upsilon \nu \left( {2{x^2}} \right)}}{{1 - \sigma \upsilon \nu \left( {3{x^2}} \right)}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\lim_{x\rightarrow 0}\frac{x-sinx}{x^{3}}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\lim_{x\rightarrow 0}\frac{x-ln(x+1)}{x^{2}}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{ \lim_{x\rightarrow 0}\frac {1 - \cos ax \cos bx \cos cx}{x^2}}$ από Αναστάσιο Κοτρώνη
$\displaystyle{\mathop {\lim }\limits_{x \to 0} \left( {\frac{1}{x} - \frac{{\eta \mu x}}{{x^2 }}} \right)}$ από Γιώργο Τσικαλουδάκη
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left( {x - x^2 \eta \mu \frac{1}{x}} \right)}$ από Γιώργο Τσικαλουδάκη
$\displaystyle\lim_{x\to\infty}\frac{x+sinx}{x-sinx}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\lim_{x\rightarrow \frac{\pi}{2n}}(\frac{sinx}{sin\pi/2n})^{\frac{1}{cosnx}}}$ από antegeia
$\displaystyle{\lim_{x\rightarrow\frac{\pi}{4}^+}(\frac{sinx+cosx}{\sqrt2})^{\frac{1}{\sqrt{x-\pi/4}}}}$ από antegeia
$\displaystyle{\lim_{x\rightarrow\frac{\pi}{2}^+}\frac{tanx-ln(x-\frac{\pi}{2})}{x-\frac{\pi}{2}}}$ από antegeia
$\displaystyle\mathop {\lim }\limits_{x \to +\infty } \left( 1+\frac{1}{x}\right)^x}$ από KapioPulsar
$\displaystyle{\lim_{x\rightarrow 0}\frac{\sqrt{cosx}-\sqrt[3]{cosx}}{1-cos^2x}}$ από erxmer
$\displaystyle{\displaystyle{\lim_{x \to 0}\frac{sinx}{\sqrt{1-cosx}}}}$ από erxmer
$\displaystyle\lim_{x\rightarrow 1^{+}}\frac{xlnx}{x-1}$ από mixalis_i
$\displaystyle{\lim_{t\rightarrow+\infty}\displaystyle\frac{\ln (t+\sqrt{t^{2}+1})}{\ln t}}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\lim_{x\to a}\frac{x^a-a^x}{x^x-a^a}}$ από Αναστάσιο Κοτρώνη
$\displaystyle{\mathop {\lim }\limits_{x \to 0} \frac{{x - \eta \mu x}}{{x^2 }}}$ από Γιώργο Τσικαλουδάκη
$\displaystyle{\lim_{x \to 0}\frac{ln(x+1)+e^x-cos2x}{(1-sinx)^2-e^x}}$ από erxmer
$\displaystyle{\lim_{x \to \frac{\pi}{2}}(sinx)^{tanx}}$ από erxmer
$\displaystyle{\lim_{x \to 0}(1+tanx)^\displaystyle{{\frac{1}{tanx}}}}$ από erxmer
$\displaystyle\lim_{x \to 7}\frac{\sqrt{x+2}-\sqrt[3]{x+20}}{\sqrt[4]{x+9}-2}$ από irakleios
$\displaystyle{\lim_{x\to a}\frac{\sin^2x-\sin^2a}{x^2-a^2}}$ από irakleios
$\displaystyle{\lim_{x\to 0}\frac{e^x-1}{x}}$ από irakleios
$\displaystyle{\lim_{x\to 0}\frac{a^x-1}{x},0 < a\neq 1}$ από irakleios
$\displaystyle{\lim_{x\to 1}\frac{x^m-1}{x^n-1},\, m,n\in N}$ από irakleios
$\displaystyle{\lim_{x\to 0} (\cos x)^{\displaystyle\frac{1}{\sin^2x}}}$ από irakleios
$\displaystyle{\lim_{x\to 0}x(\ln(x+1)-\ln x)}$ από irakleios
$\displaystyle{\lim_{x \rightarrow +\infty}\left(e^{x}-\frac{x^{2}}{2}-x+lnx \right)}$ από dopfev
$\displaystyle{ \lim_{x \to 0}{\frac{x - sinx}{x^3}}}$ από irakleios
$\displaystyle{\underset{x\to 0}{\mathop{\lim }}\,\frac{\tan \alpha x}{\tan \beta x}, \alpha\beta \ne 0}$ από ghan
$\displaystyle \lim_{x \to 0^{+}}\frac{x-x\sigma \upsilon \nu x}{x-\eta \mu x}$ από g.liolios

Όρια στο άπειρο
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \frac{{x^{k + 8} + 2001}}{{4x^{2k + 4} - x^{12} + 2001}}, k \in N }$ από Κώστα Τηλέγραφο
$\displaystyle{\begin{gathered}\mathop{\lim }\limits_{x\to +\infty }\sqrt{\frac{{x-\cos^{2}x}}{{x+\sin x}}}\hfill\\ \mathop\ \end{gathered} }$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\lim\limits_{x\rightarrow\infty}\left( a\sqrt{x+1}+b\sqrt{4x+1}+c\sqrt{9x+1}\right),a,b,c\in R}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle \mathop {\lim }\limits_{x \to \infty } \frac{{\alpha + \eta \mu [\ln (x + \beta )]}}{{\alpha + \eta \mu (\ln x)}},\alpha \notin \left[ { - 1,1} \right]$ από Βασίλη Μαυροφρύδη (mathxl)
$\mathop {\lim }\limits_{x \to + \infty } \left[ {x\left( {\sqrt {{x^2} + 1} - \sqrt[3]{{{x^3} + 1}}} \right)} \right]$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{\lim_{x\rightarrow +\infty}\frac{e^{x}-e^{-x}+2}{e^{x}+e^{-x}+3}}$ από skywalker13
$\displaystyle{ \lim_{x\rightarrow +\infty }(\sqrt{7x^{4}+6x+5}-\sqrt{7x^{4}+3x+3}) \sqrt{63x^{2}-5x+20}$ από Χρήστο Στραγάλη
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left( {2x\eta \mu \frac{1}{x} - x\eta \mu \frac{2}{x}} \right) }$ από Γιώργο Τσικαλουδάκη
$\displaystyle{\mathop {{\rm{ }}\lim }\limits_{x \to + \infty } \left( {2x^3 \eta \mu \frac{1}{x} - x^3 \eta \mu \frac{2}{x}} \right) }$ από Γιώργο Τσικαλουδάκη
$\displaystyle{\lim_{x\rightarrow +\infty}\left(\frac{5cosa-\sqrt{7}sina}{8}\right)^x ,a\in\left(-\frac{\pi}{4},\frac{\pi}{4}\right)}$ από erxmer
$\displaystyle{\lim_{x\rightarrow +\infty}\frac{2^x\eta \mu x-7^{x+1}}{\lambda ^x+5^x},\lambda > 0}$ από erxmer
$\displaystyle\lim_{x\to +\infty}(2010^{\frac {1-x}{x}}+2010^{\frac {2-x}{x}}+...+2010^{\frac {2010-x}{x}})$ από Σπύρο Καπελλίδη
$\displaystyle{\lim_{x\rightarrow -\infty }\frac{3^{2x}}{2^{3x}}}$ από mixalis_i
$\displaystyle{\lim_{x\to \infty} \left ({\sqrt{x^2+ax+c}+\sqrt{x^2+bx+d}-2x}\right)}$ από irakleios
$\displaystyle{\lim_{x \to + \infty } \left( {x^\nu \cdot \eta \mu \left( {1 - \sigma \upsilon \nu \frac{1}{x}} \right)} \right),\nu \in Z}$ από Στάθη Κούτρα
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left[ {\left( {5x^3 \eta \mu \left( {\frac{2}{x}} \right) + x^2 + x} \right) \left( {\sqrt[3]{{x^3 + 1}} - x} \right)} \right]}$ από Στάθη Κούτρα
$\displaystyle{\lim_{x \rightarrow +\infty}(1 + \frac{1}{ax}) ^ x,a >1}$ από onedeadslime
$\displaystyle {\lim_{x \rightarrow -\infty}e^{\displaystyle \frac{x^{3}sin(\frac{2}{x})}{x^{2}+1}}}}$ από Christiano
$\displaystyle {\lim_{x \rightarrow +\infty} (4^{x}sin(\frac{1}{3^{x}}))}$ από Christiano
$\displaystyle{\mathop {\lim }\limits_{x \to \pm \infty } \frac{{a^x + 2^{x + 1} }}{{a^{x + 1} + 2^x }},a > 0}$ από Σπύρο Καρδαμίτση
$\displaystyle{\lim_{x\rightarrow +\infty}\frac{\sigma \upsilon \nu x}{lnx}}$ από parmenides51
$\displaystyle{\lim_{x\rightarrow +\infty}(2x-3\eta \mu x)}$ από parmenides51
$\displaystyle{\lim_{x\rightarrow\\+\infty}{(e^x - x)}}$ από irakleios
$\displaystyle{\lim_{x\rightarrow\\+\infty}\frac{\sqrt{x-3}}{\sqrt x - 3}}$ από irakleios
$\displaystyle{\lim_{x\rightarrow +\infty}\eta\mu x\eta \mu \left(\frac{1}{x} \right)}$ από Χρήστο Λαζαρίδη
$\displaystyle{\lim_{x\rightarrow -\infty}\left(\sigma \upsilon \nu x-1 \right)\eta \mu \left(\frac{1}{x} \right)}$ από Χρήστο Λαζαρίδη
$\displaystyle{\lim_{x\rightarrow +\infty}(\sqrt{4x^{2}-1}-\frac{2x^{2}-1}{x+2})}$ από pito
$\displaystyle{\lim_{x\to +\infty}[\sqrt{x^{2}+3x}+\sqrt{4x^{2}+5-(ax+b)]=0,a\ne 0,a,b\in R}$ από Γιώργος Κ77
$\displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,(x+1)\eta \mu (\frac{\pi x}{x+1})}$ από Βασίλη Κακαβα
$\displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,\sigma \upsilon \nu (x(x+1)\eta \mu (\frac{\pi x}{x+1})\eta \mu ((x+1)\eta \mu (\frac{\pi x}{x+1})}$ από Βασίλη Κακαβα
$\displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,\left\{ {{x}^{\frac{\lambda }{3}}}\left[ {{\left( {{x}^{2}}+1 \right)}^{\frac{1}{3}}}-{{x}^{\frac{2}{3}}} \right] \right\}}}$ από ghan (παραμετρικό)
$\displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,\frac{{{e}^{\sqrt{\ln x}}}}{\sqrt{x}}}$ από ghan
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left[ {{x^2}\left( {a\sigma \upsilon \nu \frac{1}{x} - b\sigma \upsilon \nu \frac{2}{x}} \right)} \right] = \frac{3}{2}}$ από mathxl (παραμετρικό)
$\displaystyle{\underset{n\to +\infty }{\mathop{\lim }}\,\sqrt[n]{2{{\sin }^{2}}\frac{{{n}^{1000}}}{n+1}+{{\cos }^{2}}\frac{{{n}^{1000}}}{n+1}}}$ από ghan
$\displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,{{\left( 1+\frac{x-2}{{{x}^{2}}+1} \right)}^{\frac{{{x}^{3}}-1}{{{x}^{2}}+1}}}$ από orestisgotsis

Όρια με de l' Hospital
Μεταφέρθηκαν όλα στο Bulletin Διαφορικός Λογισμός

Δίνεται συνέχεια σε σημείο, ζητείται συνέχεια αλλού
$\displaystyle{f(x+y)=xf(y)+yf(x)}$ νδο $\displaystyle{f}$ συνεχής στο $\displaystyle{(0,+\infty)}$ αν $\displaystyle{f}$ συνεχής στο $\displaystyle{ 1}$ από Φωτεινή Καλδή
$\displaystyle{f(x+y)=f(x)+f(y)+xy(x+y)+k}$ vδο $\displaystyle{f}$ συνεχής στο $\displaystyle{R}$ αν $\displaystyle{\lim_{x\rightarrow 0} \frac{k+f(x)}{x}=k\in R}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f\left( {x - 2y} \right) = f\left( x \right) - 2f\left( y \right)}$ νδο $\displaystyle{f}$ συνεχής στο $\displaystyle{R}$ αν $\displaystyle{f}$ συνεχής στο $\displaystyle{ 2010 }$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x+y)=f(x)cos(2y) + f(y)cos(2x)}$ νδο $\displaystyle{\lim_{x \rightarrow a}\frac{f(x)-f(a)}{x-a}=cos2a}$ αν $\displaystyle{\lim_{x \rightarrow 0}\frac{f(x)}{x}=1}$ από harinho7
$\displaystyle{f(xy) = f(x)f(y)}$ νδο $\displaystyle{f}$ συνεχής στο $\displaystyle{R^ *}$ αν $\displaystyle{f}$ συνεχής στο $\displaystyle{ a\in R^ *}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(f(x))=4x-3}$ , νδο $\displaystyle{\lim_{x \rightarrow 1}\frac{f(x)}{x^{2}-2x+1}=+\infty}$ αν $\displaystyle{f}$ συνεχής στο $\displaystyle{ 1}$ από Christiano
$\displaystyle{f\left( x+y \right)=\frac{f\left( x \right)+f\left( y \right)}{1-f\left( x \right)\cdot f\left( y \right)},\left( x \right)\cdot f\left( y \right)\ne 1$ , νδο $\displaystyle{f}$ συνεχής στο $\displaystyle{R}$ αν $\displaystyle{f}$ συνεχής στο $\displaystyle{ 0}}$ από ghan
$\displaystyle{f\left( x+y \right)=f\left( x \right) f\left( y \right)}$ νδο $\displaystyle{f}$ συνεχής στο $\displaystyle{R}$ αν $\displaystyle{f}$ συνεχής στο $\displaystyle{a}$ από ghan

Συνέχεια συνάρτησης
$\displaystyle{f^{-1}(x)=\frac{1}{f(x)},x\in\left[\frac{1}{\alpha},\alpha\right]}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f^3 (x) + f(x) = 2e^x}$ από hsiodos
$\displaystyle{f^3(x) + f(x) + 2 = x}$ από Kagias
$\displaystyle{f(x)=\sqrt{x^4-x^2}}$ από Κώστα Σερίφη
$\displaystyle{f(x) = \left\{ {\begin{matrix} {\frac{{\sqrt {1 - \cos \left( {{x^2}} \right)} }}{{1 - \cos (x)}}} & {,x \in \left[ { - \sqrt {\frac{\pi }{2}} ,\sqrt {\frac{\pi }{2}} } \right]- \left\{ 0 \right\}} \\ a & {,x = 0} \\ \end{matrix}} \right.}$ από papel
$\displaystyle{f(x)=\begin{cases} x^2+5 & \text{ ,} x \notin Z \\ 2 & \text{ ,} x \in Z \end{cases}}$ από Φωτεινή Καλδή
$\displaystyle{f(x+y)\leq f(x)+f(y)}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)=\begin{cases} -1 & , x \in Q \\ 0 & , x \in R-Q \end{cases}}$ από bokalos (Dirichlet)
$\displaystyle{(f(x))^4 + (g(x))^2 + x \le 2f(x)g(x) + x^2 }$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x)=\begin{cases} & \text {x-1 } , x<0 \\ & \text {cosx} , x\geq 0 \end{cases}}$ από Νίκο Ζαφειρόπουλο
$\displaystyle{g(x) = f(x) \eta \mu x,h(x) = f(x) \sigma \upsilon \nu x}$ συνεχείς από Χρήστο Καρδάση
$\displaystyle{\left| {f(\alpha ) - f(\beta )} \right| \ge \left| {\alpha - \beta } \right|}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{3f(x)=2x+\sin f(x)}$ από Στράτη Αντωνέα (εδώ κι εδώ)
$\displaystyle{f^3 (x) + 3f(x) = 3x}$ από Γιώργο Τσικαλουδάκη
$\displaystyle{f(x)+f(f(x))=2005,f(4)=3}$ από kost65
$\displaystyle{cos(f(x)-f(y)) \ge cox(x-y)}$ από Σπύρο Καπελλίδη
$\displaystyle{(f\circ f)(x)=x+sinx+a}$ από Σπύρο Καπελλίδη
$\displaystyle{ f:\left[ {0,1} \right]\to Q,f\left( \frac{1}{2}\right) = \frac{1}{2}}$ από Χρήστο Κυριαζή (chris_gatos) (ρητοί)
$\displaystyle{sinf(x)=1}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)f(f(x)) = 2,f(8) = 5}$ από Χρήστο Κυριαζή (chris_gatos) (υπάρχει και συνεχής και ασυνεχής)
$\displaystyle{\sin f(t) + tf(t) = \varphi(t), \forall t \in (1,+\infty),χ>1}$ από socrates
$\displaystyle{(f(x)-f(y))(yf(x)-xf(y))\leq 0, x,y>,f}$ μονότονη από Νίκο Απστολάκη
$\displaystyle{\left\{ {f(1),f(2),f(3),...,f(100)} \right\} = \left\{ {g(1),g(2),g(3),...,g(100)} \right\}}$ από Νίκο Ζανταρίδη
$\displaystyle{f(x + \frac{1}{n}) + f(x + \frac{2}{n}) + ... + f(x + \frac{{n - 1}}{n}) = (n - 1)f(x)}$ από Νίκο Ζανταρίδη (περιοδική)
$\displaystyle{h\left( x \right) = \max \left\{ {f\left( x \right),g\left( x \right)} \right\}}$ από Βασίλη Μαυροφρύδη (mathxl) (συνάρτηση max)
$\displaystyle{f(x)\geq x, x \in R, f^{-1}(x)\geq lnx +1 ,x>0}$ από Παναγιώτη Γκριμπαβιώτη
$\displaystyle{f^{2}(x) \le 4xf(x)-3x^{2}}$ από Christiano
$\displaystyle{f(2^x-3x)=2^{f(x)}-3f(x)}$ από Ροδόλφο Μπόρη

Ερωτήσεις στην συνέχεια
συνεχής συνάρτηση - μια απλή ερώτηση από Κώστα Σερίφη
σωστό λάθος από Σπύρο Καρδαμίτση
αντίστροφη από coheNakatos
συνεχής συνάρτηση από Χρήστο Κυριαζή (chris_gatos)
πόσες μονάδες χάνει η παρακάτω λύση από Κώστα Τηλέγραφο
σωστό λάθος από Γιώργο Τσικαλουδάκη
σύνθεση ασυνεχών συναρτήσεων από Ανδρέα Πούλο
είναι συνεχής; από Θωμά Ραϊκόφτσαλη
συνέχεια από sxima
υπάρχει αντιπαράδειγμα για την fofof; από Ανδρέα Πούλο
αναζήτηση ασυνεχών συναρτήσεων από teo
συνεχής συνάρτηση από Χρήστο Κυριαζή (chris_gatos)
κάθε τιμή δυο φορές από Pla.pa.s
συνέχεια στα άκρα διαστήματος από Θωμά Ποδηματά
κι άλλο αυτονόητο από Βασίλη Κακαβα
παντού ασυνεχής από Σπύρο Καπελλίδη (εδώ, εδώ, εδώ)
όριο και συνέχεια σύνθετης από dennys
συνέχεια και αντίστροφη συνάρτηση (απορία) από djuser1911
Σ-Λ, ακατάλληλο για ανήλικους από Μπάμπη Στεργίου
σωστό - λάθος στη συνέχεια από nik21
2 ερωτήσεις για τα μαθηματικά κατεύθυνσης από Δημήτρη Κατούνη

Θεωρητικές στην συνέχεια
συνέχεια συνάρτησης από Χρήστο Κυριαζή (chris_gatos)
μια με συνέχεια ρίζας από Νίκο Μαυρογιάννη
υπάρχουν; πραγματικές συναρτήσεις ΙΙ από Απόστόλη Παπαδογιαννάκη
μέγιστο - ελάχιστο από Κώστα Σερίφη
σταθερή συνάρτηση από Βασίλη Μαυροφρύδη (mathxl)
συνεχής και όχι 1-1 από Βασίλη Μαυροφρύδη (mathxl)
συνεχής συνάρτηση από Βασίλη Μαυροφρύδη (mathxl)
συνέχεια ρίζας από Νίκο Μαυρογιάννη
απλή εκφώνηση από gemar99
συνεχής συνάρτηση από Χρήστο Ντάβα
σταθερή συνάρτηση από Σπύρο Καπελλίδη (max)
διάστημα κλειστό και φραγμένο από Σπύρο Καπελλίδη
ας τα προσέξουμε από Μπάμπη Στεργίου
αντίστροφη από coheNakatos
συνάρτηση δυο προς ένα από teo
μέγιστη τιμή συνάρτησης από Σπύρο Καρδαμίτση
συνεχής κ 1-1 είναι γν. μονότονη από Σήφη Ξυδάκη
υπάρχει; από Χρήστο Κυριαζή (chris_gatos)
συνεχείς συναρτήσεις - ακριβώς 2 ρίζες από Mulder
τοπικό μέγιστο σε δύο σημεία διαστήματος από Χρήστο Κυριαζή (chris_gatos)
συναρτήσεις από Σπύρο Καπελλίδη
όριο από socrates
1-1 και επί από Σπύρο Καπελλίδη
ύπαρξη μονοτονίας από Pla.pa.s
συνάρτηση συνεχής και επί από Σπύρο Καπελλίδη
λάθος ζητούμενο ή λάθος άσκηση από Βασίλη Κακαβα
συνεχής συνάρτηση και μονοτονία από Μπάμπη Στεργίου
ένα αυτονόητο από Βασίλη Κακαβα και Μπάμπη Στεργίου
ελάχιστο στο R από Σπύρο Καρδαμίτση
κάθε τιμή ακριβώς δύο φορές από socrates
έχει ελάχιστο δεν είναι 1-1 από Βασίλη Κακαβα
συνέχεια και αντίστροφη συνάρτηση (απορία) από djuser1911
συνεχής συνάρτηση από Σπύρο Καπελλίδη (συνάρτηση min, max)
όχι διάστημα,αλλά ένωση από Φωτεινή
μία ωραία με σταθερό σημείο από chris_gatos

Δεν υπάρχει συνεχής συνάρτηση
$\displaystyle{1+f(x) + f(x)f(2008+x) = 0 }$ από Μπάμπη Στεργίου
$\displaystyle{f\left( x \right) + f\left( {x^2 } \right) = x,x \in \left[ {0,1} \right]}$ από chris_gatos
$\displaystyle{f(1)f(2) f(3) \cdot ... \cdot f(2050) = - 1,f^2 (x) > x^2 + 1}$ από Σπύρο Καρδαμίτση
$\displaystyle{f^{2}(x)-2f(x)\sigma \upsilon \nu [f(x)]+1=0}$ από Στέλιο Μαρίνη
$\displaystyle{f(x+y)+f(f(x)+f(y))=f(f(x+f(y)))+f(y+f(x)),x,y>0, f(x)>0, f\downarrow}$ από Σπύρο Καπελλίδη
$\displaystyle{(f \circ f)(x)=2f(x)-5x}$ από Σπύρο Καπελλίδη
$\displaystyle{[f(x)]^3+af(x)=x, a<0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(f(x))=x^2-4x+6, f(2)=3}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)+f(f(x))=2005,f(4)=3}$ από kost65
$\displaystyle{\left|f(x) - f(y) \right|\geq \sqrt{\left|x-y \right|}}$ από Νίκο Ζανταρίδη
$\displaystyle{x^{2} \leq f(x) \leq x^{2} + 1, f}$ μονότονη από Ανδρέα Πούλο
$\displaystyle{f(a)=a+1,f(f(x))=(x-a)^2+a}$ από Σπύρο Καπελλίδη
$\displaystyle{f(f(x))=\frac{1}{x},x>0,f(x)>0}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x)f(f(x)) = 2,f(8) = 5}$ από Χρήστο Κυριαζή (chris_gatos) (υπάρχει και συνεχής και ασυνεχής)
η εξίσωση $\displaystyle{f(x)=c}$ να έχει ακριβώς δύο ρίζες από Mulder (εδώ κι εδώ) (δεν υπάρχει συνεχής που παίρνει κάθε τιμή της ακριβώς δυο φορές)
$\displaystyle{f^3(x)+f^2(x)= x+24}$ από Κώστα Μπουμπουλή
$\displaystyle{fog\uparrow, gof\downarrow}$ από Κώστα Σερίφη
$\displaystyle{x^a \left(f\left(\frac {2x+3}{x+1}\right)-f\left(\frac {2x+1}{x}\right)\right)=2011, x>0,a \in (0,1]}$ από Νίκο Ζανταρίδη
$\displaystyle{f\left(\frac{x}{1+x}\right)=x+f(x),x>0}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(0) = 0,f(a) = a,f^3 (x) - f(x) = x^2 - x, x \in [0,a]}$ από Χρήστο Λαζαρίδη (εδώ)
$\displaystyle{ 2f^{3}(x)-3f(x)=2x+3}$ από Δημήτρη Ιωάννου
$\displaystyle{f(x)\Q \Leftrightarow f(x+1)\in R-Q}$ από gtk1994 (ρητοί άρρητοι)
$\displaystyle{f(f(x))=(x-a)^2+a}$ από Μπάμπη Στεργίου
$\displaystyle{f(f(x))<f(x),x \in [0,1] }$ από Γιώργος Κ77

Εύρεση συνεχούς συνάρτησης
$\displaystyle{f(2x-f(x))=x, f(\xi)=\xi, f}$ 1-1 από mostel
$\displaystyle{f(2x)=f(x)}$ συνεχής στο $\displaystyle{0}$ από Αναστάσιο Κοτρώνη
$\displaystyle{K(x+ψ)=K(x)+K(y), K(x)=cx,f(x+y)=g(x)+h(y)}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x+y)=f(x)f(y)+f(x)+f(y)}$ από socrates
$\displaystyle{\left| {f(x) - f(y)} \right| \ge \left| {x - y} \right|,x,f(x)\in [0,1]}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{\left| {f(x) - f(y)} \right| \ge \left| {{2^x} - {2^y}} \right|,x,f(x)\in [0,1]}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{f(xy) \geq f(x)f(y) \geq (xy)^}$ από Φωτεινή Καλδή
$\displaystyle{f(f(x))=x}$ από Φωτεινή Καλδή
$\displaystyle{f(2x-f(x))=x,f(a)=a,f}$ 1-1 από peter
$\displaystyle{{f^2}(x) + 6x = {x^2} + 9}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{(h(x)-f(x))(h(x) - g(x)) = 0}$ από Μπάμπη Στεργίου (φυλλάδιο)
$\displaystyle{f(x + \frac{1}{n}) = f(x),χ\in Q, n\in N^*}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x)f(y)=f(\sqrt{x^2+y^2})}$ από Μπάμπη Στεργίου
$\displaystyle{f(x_{1})+f(x_{2})+f(x_{3})=f(y_{1})+f(y_{2})+f(y_{3})}$ με $\displaystyle{x_{1}+x_{2}+x_{3}=y_{1}+y_{2}+y_{3}=0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)f(ax)=e^x, a \in (0,1)}$ από socrates
$\displaystyle{f^{2}(x)-2f(x)\sigma \upsilon \nu [f(x)]+1=0}$ από Στέλιο Μαρίνη
$\displaystyle{f{f(x)-2f(y)+f(z)=0}$ με $\displaystyle{x-2y+z=0}$ από Φωτεινή Καλδή
$\displaystyle{f(x+y+1) =f(x) + f(y), f(0)=1}$ από polysot
$\displaystyle{f(f(x))=\frac{1}{2}(1+ln(1+e+e^{1+2x}),\lim_{x\to -\infty}f(x)=\frac{1}{2}}$ από Ροδόλφο Μπόρη (με δεδομένο όριο)
$\displaystyle{f(f(f(x)))+f(x)=2x}$ από Θάνο Μάγκο (matha)
$\displaystyle{f(g(x+y))=g(f(x)+f(y)),g}$ 1-1 από Σπύρο Καπελλίδη
$\displaystyle{f(x)+y=f(x+f(y))}$ από Σπύρο Καπελλίδη
$\displaystyle{f^2(x) - 2f(x)=e^{2x} -1,f(x)>1}$ από Vkalf
$\displaystyle{f(x+g(y))=y+g(x) ,f(1)<f(2)}$ από Ροδόλφο Μπόρη
$\displaystyle{f(2x) = f(x)}$ από Πέτρο Χρονόπουλο (Μαθηματικός)
$\displaystyle{f(x)+f^{-1}(x)=2x}$ από Νίκο Αποστολάκη (όχι λυκειακό)
$\displaystyle{g(2x) = g(x) + x,g}$ συνεχής στο $\displaystyle{0}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{3f\left(x \right)=f\left(\frac{x}{2} \right)+f\left(\frac{x}{3} \right)}$ από Νίκο Ζανταρίδη
$\displaystyle{g(x)=\frac{1}{3}g(x^{2})+\displastyle\frac{1}{4}g(1-x^{2}}),x \in [0,1]}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{99f\left( x \right) = f\left( {\frac{x}{2}} \right) + f\left( {\frac{x}{3}} \right) + ... + f\left( {\frac{x}{{100}}} \right)}$ από Νίκο Ζανταρίδη
$\displaystyle{{f^2}(x) = 7f(x) - 10}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{f(x)=f(\frac {x}{1-x})}$ συνεχής στο $\displaystyle{0}$ από Νίκο Ζανταρίδη
$\displaystyle{\forall n \in N^* \wedge \forall x_1,x_2,...,x_n \in [0,1] : x_1+x_2+...+x_n=1 \Rightarrow f(x_1)+f(x_2)+...+f(x_n)=1}$ από Νίκο Ζανταρίδη
$\displaystyle{x^2f(x)=f(x^2)}$ από socrates
$\displaystyle{f(x)f(f(x)) = 2,f(8) = 5}$ από Χρήστο Κυριαζή (chris_gatos) (υπάρχει και συνεχής και ασυνεχής)
$\displaystyle{f(f(x))=e^{x}}$ από Γιώργο Απόκη
$\displaystyle{f(x^2+y^2)=xf(x)+yf(y)}$ από Μπάμπη Στεργίου
$\displaystyle{\underbrace {f\left( {f\left( {...f\left( x \right)...} \right)} \right)}_{\nu - \varphi o\rho \varepsilon \varsigma } = x, x,f(x) \in \left[ {0,1} \right],f(0)=0}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x+y)=2010^xf(y)+2010^yf(x), f (1) = 2010}$ από erxmer
$\displaystyle{f\left( {x + y} \right) = yf(x) + f\left( {f(x)} \right)}$ από Γιώργο Τσικαλουδάκη
$\displaystyle{f^2(x)-5f(x)+6=0}$ από Γιώργο Απόκη
$\displaystyle{f(x+y)=f(x)+f(y)+f(x)f(y)}$ από Ροδόλφο Μπόρη

παίρνει μόνο ακέραιες τιμές, f(1)=4

από Λευτέρη Πρωτοπαπά
$\displaystyle{f(ax+x)=f(ax)a^x,a>1,f(x)>0}$ από Σπύρο Καπελλίδη
$\displaystyle{f^2(x)=(e^x+1)^2}$ από parmenides51
$\displaystyle{f^2(x)=(e^x-1)^2}$ από parmenides51
$\displaystyle{f(x)+f(y)=f(f(x)+y), x,y \in [0,1] \wedge f(x)+y \in [0,1],f:[0,1] \to [0,1]}$ από Σπύρο Καπελλίδη
$\displaystyle{ \displaystyle{(x-2)f(x)=e^x\eta \mu (x-2)}}$ από parmenides51
$\displaystyle{y^2f(x) + f(xy^2) = 2yf(xy)}$ από socrates
$\displaystyle{2^{y+1}f(x)+2^{x+1}f(y) = f(x+y)+4^yf(x-y)}$ από socrates
$\displaystyle{f\left( x \right) - f\left( {\frac{x}{2}} \right) + \frac{1}{4}f\left( {\frac{x}{4}} \right) = 2x,x \in \left[ {0,1} \right]}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f\left(\left|x\right|\right)\left|f(x)\right|=x^2}$ από Σπύρο Καπελλίδη
$\displaystyle{g\left(\left|x\right|\right)+\left|g(x)\right|=2\left|x\right|}$ από Σπύρο Καπελλίδη
$\displaystyle{\left|x^{2}f(y)-y^{2}f(x) \right|\leq x+y,x,y\geq 0,f(1)=1}$ από Γιώργος Κ77
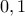$\displaystyle{f(x)=f(x^{2})}$ συνεχής σε $\displaystyle{0,1}$ από pito
$\displaystyle{2f(x) + f(y) = 3f(\frac{2x+y}{3}),x \in [0, 1],f(0) = f(1) = 0}$ από erxmer
$\displaystyle{\frac{1}{2}f(xy)+\frac{1}{2}f(xz)-f(x)f(yz) \geq \frac{1}{4}}$ από erxmer
$\displaystyle{f(x) = f(x^2 + c),c>0}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x-y)f(y-z)f(z-x)+8=0}$ από erxmer
$\displaystyle{xf(f(x))=f^2(x),x>0,f(x)>0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)=f(2x)}$ από Christiano
$\displaystyle{f(x^2)-f(y^2)=(x+y)f(x-y)}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x^3) \ge x^2f(x),f(2x) \le x+f(x),f(0)=0,f(1)=1}$ από Σπύρο Καπελλίδη
$\displaystyle{ {k\left( {x + y + z} \right) = f\left( x \right) + g\left( y \right) + h\left( z \right)}}$ από Σωτήρη Λουρίδα

Εύρεση τιμής συνεχούς συνάρτησης
$\displaystyle{f(f(x)) + f(x) = 10,f(1) = 2,f(7,999)=?}$ από Χρήστο Λαζαρίδη
$\displaystyle{f(f(x))=a\ f(x)+b \ x,0<a,b<1/2,f(0)=?}$ από Σπύρο Καπελλίδη
νδο $\displaystyle{\exists a \in [2,3): f(R)= [\frac{1}{a}, a]}$ εαν $\displaystyle{f(x) f(f(x))=1, f(3)= \frac{1}{2}}$ από Κώστα Σερίφη
$\displaystyle{f(x)\R-Q,x\in [0,1], f(0)=\sqrt{3}, f(1)=?}$ από nassou13
$\displaystyle{f(x)f\left(\frac{-1}{x}\right)=-1,x\neq 0,f(0)=?}$ από Παναγιώτη Γκριμπαβιώτη
$\displaystyle{f\left( {f\left( x \right)} \right) = {\left( {x - \alpha } \right)^2},a\in [0,\infty), a=?}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x) f\left( {f(x)} \right) = 5,f(10)=9,f(2)=? }$ , από Θωμά Ραϊκόφτσαλη (εδώ , εδώ κι εδώ) (γενίκευση)
$\displaystyle{f(x)f(f(x))=2,f(8)=5,f(2),f(3),f(4)=?}$ από Δημήτρη Ιωάννου
$\displaystyle{\mathop {\lim }\limits_{x \to 1} f(x) = \ell \in \R}$ όταν $\displaystyle{e^{f(x)} + f(x) = \ln x}$ από Σπύρο Καρδαμίτση
$\displaystyle{f(f(x))+4f(x)=6-x^{4}}$ από pito
$\displaystyle{f^2(x)+f(f(x))=x^2-x+1}$ από Μπάμπη Στεργίου

Σύνολο τιμών συνεχούς συνάρτησης
μέγιστο - ελάχιστο από Κώστα Σερίφη (Αν μια συνεχής στο (α,β) συνάρτηση έχει όρια στα α,β ή τότε θα έχει μέγιστο ή ελάχιστο αντίστοιχα)
$\displaystyle{ |f(x)-f(y)|\geq|x-y|}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f^3 (x) + f(x) = 2e^x}$ από hsiodos
$\displaystyle{f(2)>0,f(-1)<0,f^2(x)\ge x^2}$ από Ροδόλφο Μπόρη
$\displaystyle{f(x)=(g(x)-x)^{2}+4, g(1)<1,g(2)>2 }$ από tsolis
νδο $\displaystyle{\exists a \in [2,3): f(R)= [\frac{1}{a}, a]}$ εαν $\displaystyle{f(x) f(f(x))=1, f(3)= \frac{1}{2}}$ από Κώστα Σερίφη
$\displaystyle{f\left( x \right) e^{f\left( x \right)} = x}$ από Μάκη Χατζόπουλο
$\displaystyle{f(x)\,e^{f(x)} \geq x^2-100,f(10)=0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)=-x+\sqrt{1+x^2}}$ από dennys
$\displaystyle{f(x)=\sigma \upsilon \nu ^{2}x+2^{x+1}\eta \mu x-4^{x}}$ από Δημήτρη Ιωάννου
$\displaystyle{f^3(x)+f^2(x)= x+2}$ από Κώστα Μπουμπουλή
$\displaystyle{f^{3}(x)+f(x)+1=x}$ από margk
$\displaystyle{f(x) = 2 - x - x^5}$ από pastavr

Ερωτήσεις πάνω στα θεωρήματα συνεχών
θεώρημα Bolzano από cos70
ερώτηση Α Ψ από Μίλτο Παπαγρηγοράκη
σύνολο τιμών από Γιώργο Ασημακόπουλο
θεώρημα ενδιαμέσων τιμών και σύνολο τιμών από ma05860
ύπαρξη μονοτονίας από Pla.pa.s
επιτρέπεται η αντικατάσταση; από pito
θεώρημα μέγιστης ελάχιστης τιμής από pito
Bolzanakia από Βασίλη Ευαγγέλου
είναι τεκμηριωμένο;;; από Θωμά Ποδηματά
αληθές ή ψευδές από Σακης
απορία από Μαθηματικός
2 ερωτήσεις για τα μαθηματικά κατεύθυνσης από Δημήτρη Κατούνη

Νιοστή ρίζα
μέθοδος εύρεσης ριζικών σε ποιο διάστημα ανήκουν από Μάκη Χατζόπουλο
να αποδείξετε ότι από christodoulou
ν-ρίζα από KapioPulsar

Θεωρήματα συνεχών με γνωστό τύπο
$\displaystyle{\sin ^2 \left( {\varphi + \alpha } \right) + \sin ^2 (\varphi + \beta ) + \sin ^2 \left( {\varphi + \gamma } \right) = \frac{3}{2}}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{\sin ( \cos x) = \cos (\sin x)}$ από Δημήτρη Σκουτέρη (σύγκριση)
$\displaystyle{f(x) = \frac{{a_1 }}{{x - \rho _1 }} + \frac{{a_2 }}{{x - \rho _2 }} + .... + \frac{{a_\nu }}{{x - \rho _\nu }}}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{2\sin x + \cos 7x = 0}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{\frac{42}{x-5}+\frac{35}{x-6}+\frac{30}{x-7}=0}$ από tsolis (ακέραια ρίζα)
$\displaystyle{\frac{{\sin \left( {\frac{\pi }{5}} \right)}}{{x + 2}} + \frac{{\sin \left( {\frac{\pi }{7}} \right)}}{{x + 1}} + \frac{{\sin \left( {\frac{\pi }{9}} \right)}}{x} = 0}$ από Χρήστο Κυριαζή (chris_gatos) (ακέραια ρίζα)
$\displaystyle{x^{3}=x+1}$ από Λευτέρη Πρωτοπαπά
$\displaystyle{\lambda x^4-(3\lambda-4)x^3+3(\lambda-3)x^2-3(\lambda-2)x+2\lambda-3=0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)=ln^2{x^2} -\sqrt{x}lnx^4+x}$ από Παναγιώτη Γκριμπαβιώτη
$\displaystyle{3^{x^{3}+x+2 }+(x^{3}-3x+1) 3^{2x-3x^{3}}= 3^{4x+1}}$ από socrates (πλήθος ριζών)

Θεωρήματα συνεχών με πολλές τιμές
$\displaystyle{f(y)=\frac{f(x_{1})+\ldots+f(x_{n})}{n}}$ από Αναστάσιο Κοτρώνη
$\displaystyle{a f\left( {\frac{{2a + \beta }}{3}} \right) + \frac{{a + \beta }}{2} f\left( {\frac{{a + \beta }}{2}} \right) + \beta f\left( {\frac{{a + 2\beta }}{3}} \right) = 2004f(\xi )}$ από Χρήστο Καρδάση
$\displaystyle{ f(x_{i})=f(x_{j}) ,x_{i}\neq x_{j}}$ από Βασίλη Μαυροφρύδη (mathxl) (οχι 1-1)
$\displaystyle{|f(x_1 ) - f(x_2 )| = |x_1 - x_2 |^2}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{\left( {\kappa + \lambda + \mu } \right)f(x_o ) = \kappa f(\alpha ) + \lambda f(\gamma ) + \mu f(\beta )}$ από Σπύρο Καρδαμίτση
$\displaystyle{f(a) = f(b),a - b =2}$ από Σπύρο Καρδαμίτση (κι εδώ)
$\displaystyle{(\frac {x_1}{f(a)})^{f(x_2)}(\frac {f(b)}{x_1})^{f(x_3)}=\frac {e^{f(b)}}{e^{f(a)}}}$ από Σπύρο Καπελλίδη
$\displaystyle{{f^3}\left( {{x_4}} \right) = f\left( {{x_1}} \right) f\left( {{x_2}} \right) f\left( {{x_3}} \right)}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{|x-a_1|+|x-a_2|+\cdots +|x-a_n|=\dfrac{n}{2}}$ από Στράτη Αντωνέα (κι εδώ)
$\displaystyle{(a^{2}+1)f(b)=(b^{2}+1)f(a),a-b=1}$ από Νίκο Αποστολάκη (εδώ)
$\displaystyle f\left(x_{0} \right)=\frac{f\left(2 \right)+2f\left(3 \right)+3f\left(4 \right)}{6}$ από mixalis_i
$\displaystyle{f(1)+f(2)+f(3)=0}$ από Christiano
$\displaystyle{f(x_{0})=\frac{2f(0)+3f(\frac{1}{2})+4f(1)}{9},\kappa f(x_{1})+\lambda f(x_{2})+ \mu f(x_{3})=(\kappa+\lambda+\mu)f(\xi)}$ από Christiano
$\displaystyle{f(x_{o})=\frac{f(x_{1})+...+f(x_{n})}{n}}$ από Κώστα Καπένη (kostas136)
$\displaystyle{f(x_1)f(x_2)f(x_3)=x_1x_2x_3}$ από Κώστα Καπένη (kostas136)
$\displaystyle{f(x_1 ) + f(x_2 ) = 7,x_1 + 3x_2 = 5}$ από Σπύρο Καρδαμίτση και Βασίλη Κακαβα
$\displaystyle{f({{x}_{2}})-f({{x}_{1}})=\nu,{{x}_{2}}-{{x}_{1}}=\nu}$ από Βασίλη Κακαβα
$\displaystyle{g({{x}_{2}})-g({{x}_{1}})=1}$ από Βασίλη Κακαβα
$\displaystyle{x_{o}=\sqrt[\nu ]{x_{1}x_{2} \dots x_{\nu }}}$ από Γιώργος Κ77
$\displaystyle{a,\beta \in [-1,1]:f(a)+f(\beta )=a-\beta,f:[-1,1]\rightarrow [-1,1]}$ από pito
$\displaystyle{f(x_{0})=\frac{f(a)+2f(\frac{a+b}{2})+3f(b)}{6}}$ από Δημήτρη Ιωάννου
$\displaystyle{\left( {\alpha _1 + a_2 + ... + a_{2011} } \right)f(\xi ) = a_1 f\left( {\frac{1}{{2012}}} \right) + a_2 f\left( {\frac{2}{{2012}}} \right) + ... + a_{2011} f\left( {\frac{{2011}}{{2012}}} \right)}$ από hsiodos

Θεωρήματα συνεχών με άγνωστο τύπο
$\displaystyle{f(x)=x}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{f(x)\neq x}$ από Κωνσταντίνα Κυριακοπούλου
$\displaystyle{f(3x)>f(3x+3)}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{ (fof)(x) = x}$ από Χρήστο Καρδάση
$\displaystyle{{f^2}(x) + {g^2}(x) = c}$ από Χρήστο Λαζαρίδη
$\displaystyle{ f(1-xf(x+3))=xf(x+2)+f(x+1)}$ από Αντώνη Σπυριδάκη
$\displaystyle{|f(x)-f(y)|\leq \frac{|x-y|}{1+|x-y|}}$ από Σεραφείμ Τσιπέλη (μοναδική)
$\displaystyle{f(2) + f(x+2) = 0}$ από Σπύρο Καρδαμίτση (περιοδική)
$\displaystyle{f^2 (x) + \eta \mu ^2 x = x^2}$ από Σπύρο Καρδαμίτση
$\displaystyle{5f(1)+7f(2)=0}$ από μαριαννα
$\displaystyle{f^2 (x) + (A + B)f(x) + AB \le 0}$ από Σπύρο Καρδαμίτση
$\displaystyle{f(x)=\frac{g(x)}{a-x}+\frac{h(x)}{b-x}}$ από Σπύρο Καπελλίδη
$\displaystyle{|f(x)| \le \frac{{3x^2 + 4}}{7}}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f(x)=g(x)}$ από Χρήστο Κυριαζή (chris_gatos) (φραγμένη)
$\displaystyle{fog=gof}$ από makisman (παρόμοια)
$\displaystyle{fog=gof}$ από magkiora
$\displaystyle{f^2(x)=x^2}$ από Πέτρο Χρονόπουλο (Μαθηματικός)
$\displaystyle{ \displaystyle{g\left( {h(x)} \right) = {x^7} + x + 1 + h(x)}$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{f(x)+g(x)=0}$ από Σπύρο Καπελλίδη
$\displaystyle{a_0x+a_1f(x)+a_2f^2(x)+...+a_nf^n(x)=0}$ από Σπύρο Καπελλίδη
$\displaystyle{f(2x) > f(2x + 2)}$ από Γιώργο Τσικαλουδάκη
$\displaystyle{f(x)=x-1}$ από Χρήστο Κανάβη (pana1333)
$\displaystyle{f(f(x))=x}$ από Λευτέρη Πρωτοπαπά
$\left[ f^2(1) +4f(1)+34 \right]\left[ f^2(2)+5f(2)+73 \right]=2010$ από Αντώνη Σπυριδάκη
$\displaystyle{f\left( {f(x)} \right) +2f(x)= 2x + {x^2} }$ από Θωμά Ραϊκόφτσαλη
$\displaystyle{1-1 f(\rho)=0}$ από Βασίλη Κακαβα
$\displaystyle{f(1-f(x))-f(x)>0}$ από Βασίλη Κακαβα
$\displaystyle{f(2x-1)=-f(x+2)}$ από katsaounisgiannis
$\displaystyle{\frac{{x - \alpha }}{{f(x) - \alpha }} - \frac{{x - \beta }}{{f(x) - \beta }} = 0}$ από Γιώργο Τσικαλουδάκη
$\displaystyle{f^2 \left( x \right) + g^2 \left( x \right) = h^2 \left( x \right)}$ από Στάθη Κούτρα (εδώ)
$\displaystyle{\displaystyle{(f \circ f \circ ... \circ f)\left( x \right) = kx^m }$ από Σωτήρη Λουρίδα
$\displaystyle{f(x)(2g(x)+5) > 3}$ από Λευτέρη Πρωτοπαπά
$\displaystyle{f ( x + 3) + f ( x -1) = f (x +1) + x}$ από socrates
$\displaystyle f(x)=(x^2-4x+3)g(x)$ από Κώστα Καπένη (kostas136)
$\displaystyle{f(x ) + e^{x + 1} + \ln x = 1}$ από Σπύρο Καρδαμίτση
$\displaystyle{f^3 (x) + \beta f^2 (x) + \gamma f(x) = x^3 - 2x^2 + 6x - 1 }$ από Σπύρο Καρδαμίτση
$\displaystyle{f\left( a \right)f\left( b \right)f\left( c \right) = 1}$ από Eukleidis
$\displaystyle{f(x)=f(x+\frac{1}{2011})}$ από Γιώργος Κ77
αποδείξτε τα σχόλια του Bolzano από parmenides51
$\displaystyle{f(x)=x^3-x+3,g(x)=2x^3-4x+2}$ από KARKAR (συνευθειακά σημεία τομής)
$\displaystyle{f(x)=-3x}$ από Βασίλη Κακαβα και Μπάμπη Στεργίου
$\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \frac{{x^3 f(0) + 1}}{{x^2 + 2}} }$ από Σπύρο Καρδαμίτση
$\displaystyle{fog=gof}$ από Γιώργος Κ77
$\displaystyle{f(1)+f(2)=f(3)+f(4)}$ από Γιώργος Κ77
$\displaystyle{f^{2}\left(f\left(x \right) \right)+f\left(f^{2}\left(x \right))=2x^{2}}$ από tsiridim
$\displaystyle{f\left( x \right){e^x} = 1}$ από Eukleidis
$\displaystyle{f\bigl({\frac{\alpha}{\beta}}\bigl)\,f\bigl({\frac{\beta}{\gamma}}\bigl)\,f\bigl({\frac{\gamma}{\alpha}}\bigl)=1}$ από Ανδρεας
$\displaystyle{f\circ \ g=g\circ \ f}$ από pito
$\displaystyle{f(x)+1=x^2,2x^2-2007x+2001=0}$ από dennys
$\displaystyle{f^{2}(x)=\frac{1}{1+g^{2}(x)}}$ από Γιώργος Κ77
$\displaystyle{fog=gof}$ από Γιώργος Κ77
$\displaystyle{\mathop {\lim }\limits_{x \to \pm \infty } \frac{{f(x)}}{{{x^n}}} = 0}$ από Γιώργος Κ77
$\displaystyle{f(x)=2x^2-x+1}$ από Δημήτρη Κατούνη
$\displaystyle{fog=gof}$ από socrates

Ασκήσεις με τριώνυμα
$\displaystyle{f(x) = \alpha x^2 + \beta x + \gamma ,2\alpha +3 \gamma =0}$ από Σπύρο Καρδαμίτση
$\displaystyle{f(x) = x^2 + ax + \beta ,g(x) = - x^2 + ax + \beta ,\kappa f(x) + \lambda g(x) = 0}$ από Math Rider
$\displaystyle{f(x)=ax^2+bx+c, g((x,y))=|x|+|y|}$ από Σπύρο Καπελλίδη
$\displaystyle{ax^{2}+bx+c=0,\left|ac \right|>0,\left|a \right|-\left|b \right|+\left|c \right|<0}$ από Χρήστο Στραγαλη (ακέραιες ρίζες)
$\displaystyle{x^2+ax-b=0,0<b<a}$ από stelmarg (ακέραιες ρίζες)
$\displaystyle{ax^2 - bx + c = 0,x_1,x_2\in (0,1),(a + b + c)_{min}=?}$ από Χρήστο Κυριαζή (chris_gatos)
νδο $\displaystyle{n^2>km}$ όταν $\displaystyle{km+2mn+m^2<0,a\neq 0}$ από Λευτέρη Πρωτοπαπά
νδο $\displaystyle{b^2>4ac }$ όταν $\displaystyle{ac-bc+c^2<0,a\neq 0}$ από Αντώνη Νασιούλα
σύνθεση συναρτήσεων από dennys
$\displaystyle{fog=gof}$ από socrates

Πολυώνυμα
$\displaystyle{|f(\xi)|\leq |f(x)|}$ από Χρήστο Κυριαζή (chris_gatos)
$\displaystyle{f_{n}(x)e^{nx}+f_{n-1}(x)e^{(n-1)x}+\ldots+f_{0}(x)=0}$ από Αναστάσιο Κοτρώνη (γραμμικός συνδυασμός με εκθετικά)
$\displaystyle{f(x)=a_{5}x^{5}+a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0},a_{0}>0,}$ $\displaystyle{a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=0, 5a_{5}+4a_{4}+3a_{3}+2a_{2}+a_{1}>0}$ από Κωνσταντίνα Κυριακοπούλου
$\displaystyle{ax^{3}+bx+c=0,3a+2b+3c=0}$ από Βασίλη Μαυροφρύδη (mathxl)
$\displaystyle{f(x) + f(x+1) + f(x+2)=0}$ από Λευτέρη Πρωτοπαπά (όχι πολυωνυμική)
$\displaystyle{\lim_{x \to \infty } \frac{{1 + 2x^{345} + 6x^{789} }}{{p(x)}} = 2009}$ από papel
$\displaystyle{\lim_{x \to \,\lambda } \frac{{f(x)}}{{\left| {\,x - \lambda \,} \right|}} = 2\,\lambda - 1}$ από Χρήστο Καρδάση
$\displaystyle{a^4\beta^4= \gamma\ x^5+2(x-\beta)^4(x-a)^4,\gamma \neq 0,a < 0 < \beta}$ από Λευτέρη Πρωτοπαπά
$\displaystyle{x^6-6x^5 + 12x^4 + ax^3 + 12x^2-6x + 1}$ από erxmer
λογαριθμική από Γ. Τασσόπουλο (η λογαριθμική συνάρτηση δεν είναι πολυωνυμική)
$\displaystyle{|P(x)| \le b|Q(x)|}$ από Σπύρο Καπελλίδη
$\displaystyle{f(x)=x}$ αδύνατη στο R $\displaystyle{\Rightarrow f(f(x))=x}$ αδύνατη στο R από Παναγιώτη Γκριμπαβιώτη
$\displaystyle{x^3 + \alpha x^2 + \beta = 0,\beta > 0,\alpha + \beta + 1 < 0}$ από Σπύρο Καρδαμίτση
$\displaystyle{P(x)=\epsilon\phi x}$ από Φωτεινή
$\displaystyle{p(x)=x^5-x+a}$ από achilleas

Πρόβλημα
κλεμμένο περιδέραιο από Demetres
γεμίζουμε ένα ισόπλευρο με ίσους κύκλους από Μάκη Χατζόπουλο
ο οδοιπόρος (Bolzano) από John13
ορθογωνοποίηση των κύκλων από Μάκη Χατζόπουλο
συνέχεια και καθετότητα από Θωμά Ραϊκόφτσαλη
ο αυλικός και ο ευγενής από nonlinear
υπάρχει σημείο από Στάθη Κούτρα
ορειβασία από Γιώργο Απόκη
ανοιχτή ερώτηση από KARKAR
συναρτήσεις 2 από Γιώργος Κ77
υπαρξιακό σε τετράγωνο από Θάνο Μάγκο (matha)
γραφική παράσταση συνεχούς συνάρτησης από Σπύρο Καπελλίδη
συνέχεια συνάρτησης από dennys
απόδειξη ύπαρξης σημείου από Ανδρέα Πούλο
συναρτήσεις 11 από Γιώργος Κ77
συναρτήσεις 12 από Γιώργος Κ77
συναρτήσεις 13 από Γιώργος Κ77
το πρόβλημα με τις δύο τηγανίτες από Χρήστο Ντάβα

Ασκήσεις για επανάληψη
2009
θέμα (2) από Νίκο Αποστολάκη
το 3ο υποερώτημα λύνεται πιο εύκολα με θεωρία εντός σχ.ύλης; από Βασίλη Μαυροφρύδη (mathxl)
όριο στο άπειρο και κύκλος και χρόνια πολλά από Θωμά Ραϊκόφτσαλη
να βρεθεί το όριο από Κώστα Τηλέγραφο
θέμα 12 από Βασίλη Καλαμάτα
συναρτησιακές εξισώσεις από peter
f(f(x))=e^x από Σπύρο Καρδαμίτση
από τον διαγωνισμό εις μνήμην Β. Ξανθόπουλου από Χρήστο Τσιφάκη
συναρτησιακή και αντίστροφη από hsiodos
επαναληπτική (για να μην ξεχνιόμαστε) από Χρήστο Τσιφάκη
2010
άσκηση τη χρειάζομαι για διαγώνισμα sos από μαριαννα
συναρτήσεις από μαριαννα
άσκηση από μαριαννα
δύο συνεχείς συναρτήσεις από Σπύρο Καρδαμίτση
μια τουλάχιστον θετική ρίζα από Σπύρο Καρδαμίτση
γν. μονότονη και συνεχής από Σπύρο Καρδαμίτση
λογαριθμική και αντίστροφη από Σπύρο Καρδαμίτση
3ο - 4ο συνέχεια από Αντώνη Σπυριδάκη
βοήθεια σε άσκηση από BGNMK
f(x)e^f(x) = x ......ποια είναι η αντίστροφη της f ? από Μάκη Χατζόπουλο
άσκηση 3 από μαριαννα
όριο συνέχεια από Κώστα Τηλέγραφο
όρια συνέχεια από Γιώργο Τσικαλουδάκη
μάλλον ....θα γίνονταν το λάθος από Μπάμπη Στεργίου
συναρτήσεις όρια συνέχεια από Γιώργο Τσικαλουδάκη
με θέμα συνάρτηση από Vkalf
μονοτονία στο [1,+άπειρο) από rek2
όμορφη συνέχεια από Χρήστο Στραγάλη
άσκηση αντίστροφης συνάρτησης από kyriakh
αντίστροφη - όρια από christodoulou
συναρτήσεις όρια συνέχεια από Γιώργο Τσικαλουδάκη
άσκηση με 1-1, αντίστροφη και σύνθεση από Μάκη Χατζόπουλο και Σωτήρη Λουρίδα
άσκηση ορίων συνέχειας από τον Νίκο Ζανταρίδη
2011
αν η f έχει μοναδική ρίζα --> f(a)f(b)<0 από Παναγιώτη Γκριμπαβιώτη (PanosG)
συναρτήσεις (συνδυαστική) από erxmer
απορία για τη συνέχεια της αντίστροφης από Παναγιώτη Γκριμπαβιώτη
αντίστροφη σύνολο τιμών από Φωτεινή Καλδή
συναρτησιακή σχέση, αντίστροφη συνάρτηση, όρια από Λευτέρη Πρωτοπαπά
μονοτονία, αντίστροφη, όρια από Λευτέρη Πρωτοπαπά
μονοτονία εφαρμογή από Βασίλη Κακαβα
1-1 συνάρτηση από Σπύρο Καρδαμίτση
μονοτονία ανίσωση από Σπύρο Καρδαμίτση
μονότονη συνάρτηση από Δημήτρη Ιωάννου
εξίσωση με αντίστροφη συνάρτηση από Σπύρο Καρδαμίτση
συνέχεια από Christiano και Βασίλη Μαυροφρύδη (mathxl)
εξίσωση με αντίστροφη συνάρτηση από Σπύρο Καρδαμίτση
μάλλον απαιτητικά αλλά με στόχο από Βασίλη Κακαβα
ανίσωση με αντίστροφη από Σπύρο Καρδαμίτση
εξίσωση με αντίστροφη συνάρτηση από Σπύρο Καρδαμίτση
10 ερωτήματα σε εξισώσεις κι ανισώσεις από parmenides51
άσκηση από socrates
μια καλή επαναληπτική άσκηση από Χρήστο Κυριαζή (chris_gatos)
επαναληπτική από Γιώργο Απόκη
μονοτονία - αντίστροφη - όρια από wavelet
κλίση σε ... αναμονή από KARKAR
ένα αυτονόητο από Βασίλη Κακαβα και Μπάμπη Στεργίου
συναρτήσεις από erxmer
μονοτονία - αντίστροφη δικλαδικής από Παναγιώτη Γκριμπαβιώτη
εύρεση συνάρτησης στο γενικό μέρος από Μπάμπη Στεργίου
όριο και συνέχεια από Σπύρο Καρδαμίτση
λίγο απ' όλα από erxmer
υπολογισμός ορίων από pito
2012
όμορφη άσκηση από pito
εύρεση τιμής συνάρτησης - γενικό μέρος από Μπάμπη Στεργίου
μονοτονία - Θ.Bolzano από dennys
υπάρχει ξ από dennys
συνέχεια συνάρτησης - ρίζες από dennys
συνέχεια ... αρνήσεις από Μπάμπη Στεργίου
συναρτησιακή σχέση με αντίστροφη από Νίκο Κατσίπη (ΕΜΕ 2008, 24)
συναρτήσεις 19 από Γιώργος Κ77
συναρτήσεις 20 από Γιώργος Κ77
συναρτήσεις 24 από Γιώργος Κ77

Ασκήσεις με πολλά ερωτήματα για επανάληψη
2011
λίγο απ' όλα, χωρίς τα θεωρήματα της συνέχειας από Λευτέρη Πρωτοπαπά

Συνδυαστικές με μιγαδικούς
2009
επαναληπτική άσκηση από Χρήστο Τσιφάκη
συνάρτηση από tsolis
μιγαδικοί και συνέχεια σε κλειστό διάστημα από tsolis
θεώρημα Bolzano από tsolis
μια συνδυαστική άσκηση από το Γ1 από Βασίλη Παπαδάκη από Βασίλη Μαυροφρύδη (mathxl)
θέμα από διαγώνισμα από hsiodos
σταθερό πρόσημο από Σπύρο Καρδαμίτση
μιγαδικοί - συνέχεια από Σπύρο Καρδαμίτση
2010
συνδυαστική από Χρήστο Κυριαζή (chris_gatos)
επαναληπτική μέχρι συνέχεια από hsiodos
όρια από panathas13
ωραία ως...μπλόφα από Χρήστο Κυριαζή (chris_gatos)
εύρεση σημείου από erxmer
2011
συνεχείς συναρτήσεις από ZITAVITA
συναρτήσεις - μιγαδικοί από erxmer
συνδυαστικό με μιγαδικούς από Βασίλη Κακαβα
όρια και μιγαδικοί από Βασίλη Κακαβα
για να μην χαθεί από polysot
μετασυνεδριακή από Χρήστο Τσιφάκη

Αξιόλογες Συλλογές
2008
αρχεία από το παλιό mathematica_club στό pathfinder
2009
σωστό λάθος από Θωμά Ραϊκόφτσαλη
25 συνδυαστικές ασκήσεις στην ανάλυση - κεφάλαιο 1 από Μάκη Χατζόπουλο
συνέχεια σε κλειστό διάστημα από Θωμά Ραϊκόφτσαλη
όρια - συνέχεια Ε.Μ.Ε. (2002)
χρήσιμα από Νίκο Μαυρογιάννη
επαναληπτικό φυλλάδιο α΄β΄λυκείου για γ΄λυκείου από polysot
συνέπειες των ορισμών - χρήση χωρίς απόδειξη από Μπάμπη Στεργίου
2010
σύνθετα θέματα ορίων από Κωνσταντίνο Ρεκούμη (rek2)
πριν τη γ Λυκείου – τυπολόγιο μαθηματικών από Μίλτο Παπαγρηγοράκη
βιβλίο με ασκήσεις ανάλυσης γ λυκείου από Ροδόλφο Μπόρη
επανάληψη λυκειακής ύλης (πλην ορίων) από Μιχάλη Λάμπρου
αρχείο Bolzano από Θωμά Ραϊκόφτσαλη
μιγαδοοριακά συνεχόμενα δωράκια για τα Χριστούγεννα από xgastone
2011
μια συλλογή με παραμετρικά όρια από Κώστα Μαλλιάκα
συλλογή θεμάτων σε συναρτήσεις όρια συνέχεια (οργάνωση σε ένα αρχείο από parmenides51) (30 λυμένες)
2012
Κουίζ σε Συναρτήσεις, Όρια: μέρος 1ο, μέρος 2ο, μέρος 3ο του dimplak (online κουίζ)
2013
26 ασκήσεις στις συναρτήσεις από Δημήτρη Μυρογιάννη
Θ. Bolzano και ύπαρξη σημείων από Θανάση Κοπάδη
θεωρία 1ου κεφαλαίου από Δημήτρη Κοντόκωστα
2014
συναρτήσεις - λίγο από μέθοδο, λίγο από ασκήσεις από Νίκο Αλεξανδρόπουλο
όρια - λίγο από μέθοδο, λίγο από ασκήσεις από Νίκο Αλεξανδρόπουλο

Άξια Αναφοράς
2009
Το 3ο υποερώτημα λύνεται πιο εύκολα με θεωρία εντός σχ.ύλης; (ανισότητες και όρια στο άπειρο, μεταφέρονται;)
συναρτησιακή εξίσωση Cauchy από Demetres (Cauchy)
ανάλυση, θεωρητική - όχι για μαθητές (γνησίως μονότονη με πεδίο ορισμού και σύνολο τιμών το R άρα συνεχής)
απάντηση Α. Πετράκη στα όσα γράφτηκαν στο τεύχος 69 του Ευκλ από Βασίλη Μαυροφρύδη (mathxl)
αρκεί;; (πολλαπλότητα ρίζας)
σύστημα με αρκετό ενδιαφέρον (κι όμως λύνεται)
(παρόμοια εδώ , εδώ, εδώ , εδώ , εδώ , εδώ , εδώ)
εκθετική συνάρτηση και ελάχιστο (εντυπωσιακές ιδέες για ελάχιστο)
ιστορία βγαλμένη από την ... πραγματικότητα (βρείτε το λάθος)
προβληματισμός στον ορισμό της μονοτονίας (αντίστροφο ορισμού μονοτονίας) (κι εδώ)
συνέχεια και εύρεση τύπου (φυλλάδιο)
απορία στη βαθμολόγηση (περί βαθμολογίας)
1- κάποιοι συνάδελφοι φοβίζουν τους μαθητές 1 (τρόπος γραφής στα όρια με άπειρα)
όρια τριγωνομετρικών συναρτήσεων στο άπειρο (οι αποδείξεις) (πχ1 ,πχ2,πχ3, πχ.4.,πχ.5. )
απορία σχετικά με τη βαθμολόγηση (περί βαθμολογίας)
2010
ερώτηση πάνω σε ορισμό σχολ. βιβλίου (διατυπώσεις σχολικού)
ερώτηση Α Ψ (διατυπώσεις σχολικού)
πράξεις με σύνολα (πράξεις με σύνολα)
μια πρόσθεση (πράξεις με σύνολα)
ορισμός ακέραιου μέρους (ορισμός ακέραιου μέρους)
αντίστροφη (γνησίως μονότονη με πεδίο ορισμού και σύνολο τιμών το Δ άρα συνεχής)
σημαντικό ερώτημα(περι βαθμολογίας στην αλλαγή απάντησης στην σειρά ερωτημάτων)
χρησιμότητα bolzano (χρησιμότητα Bolzano)
είναι σωστή αυτή η διατύπωση σε ερώτηση Σ-Λ; (περί ΣΛ)
πόσες μονάδες χάνει η παρακάτω λύση (περί βαθμολογίας)
απορία (συνέχεια αντίστροφης) (η απόδειξη)
τελικά πόσο κάνει; διδακτικό επεισόδιο 2 (όρια αλα ΑΣΕΠ)
κριτήριο παρεμβολής στο άπειρο (κριτήριο παρεμβολής με μια ανισότητα στο άπειρο) (κι εδώ)
λογαριθμική (η λογαριθμική συνάρτηση δεν είναι πολυωνυμική)
2011
συνεχής κ 1-1 είναι γν. μονότονη (η απόδειξη)
είναι Σ ή Λ η παρακάτω πρόταση (ορισμός 1-1)
κυκλικές αποδείξεις (επιτρεπόμενο del' hospital σε τριγωνομετρικά όρια)
παράγωγοι; όχι, ευχαριστώ! (ακρότατα χωρίς παραγώγους)
όριο ναί (όριο ημχ/χ σε μοίρες) (κι εδώ)
να δειχθεί το όριο (κι όμως λύνεται)
εύρεση της f ^ {-1} (x) (τύπος αντίστροφης τριτοβάθμιας)
ισοδυναμία ορίων (χρήσιμη πρόταση)
συνέχεια (συνάρτηση max)
σύνθεση και πράξεις συναρτήσεων (δείτε γραφικά σύνθεση συναρτήσεων στο διαδίκτυο)
ακρότατα στην γεωμετρία χωρίς παραγώγους (ακρότατα χωρίς παραγώγους)
μονότονη συνάρτηση (μονοτονία αντίστροφης γνησίως αύξουσας και σημεία τομής αντίστροφων) (η απόδειξη)
ύπαρξη μονοτονίας (συνεχής με μονότονο περιορισμό της)
τιμές συνάρτησης (περί κέντρου συμμετρίας)
διευκρίνιση (περί αρνητικών σε υπόρριζο και μονού συνεπάγεται)
αντίστροφη συνάρτηση (σημεία τομής αντίστροφων συναρτήσεων)
2012
διδασκαλία πεδίου ορισμού και σύνολου τιμών με παράλληλη βοήθεια νέων τεχνολογίων από Κώστα Μάλλιακα

Άρθρα
νιοστές ρίζες, τα σύμβολα, σχετικά θέματα από Αντώνη Κυριακόπουλο
επισημάνσεις και διευκρινίσεις με αφορμή θέματα Πανελλαδικών εξετάσεων από Νίκο Ιωσηφίδη (7-3-07.pdf)
ορισμός ε,δ ορίου συνάρτησης από Ροδόλφο Μπόρη
μια απλή αλλά πολύ χρήσιμη πρόταση από Αντώνη Κυριακόπουλο
μέθοδοι απόδειξης και εύρεσης στα μαθηματικά από Αντώνη Κυριακόπουλο
συναρτήσεις - χρήσιμες επισημάνσεις στις βασικές έννοιες από Αντώνη Κυριακόπουλο
απόδειξη συνεπαγωγής, η ισοδυναμία από Αντώνη Κυριακόπουλο
ποσοδείκτες, προτάσεις και θέματα του τύπου: σωστό λάθος από Αντώνη Κυριακόπουλο
εύρεση συνάρτησης από Μπάμπη Στεργίου
κυβική (τριτοβάθµια) πολυωνυµική εξίσωση του Δημήτρη Αναγνώστου (τριτοβάθμια)

Πανελλαδικές Εξετάσεις
Θέματα Εξετάσεων Μαθηματικών 1974-1983 σε word
Θέματα Εξετάσεων Μαθηματικών Δεσμών 1983-2001 σε word
Θέματα Εξετάσεων Μαθηματικών ΤΕΛ 1997, 2000, 2001 σε word και pdf
Θέματα Εξετάσεων Μαθηματικών ΤΕΕ 2000-10 σε word (Ημερησίων, Εσπερινών)
Θέματα Εξετάσεων Μαθηματικών Γενικής ΓΛ 2000-10 σε word (Ημερησίων, Εσπερινών, Προαγωγικών, Επαναληπτικών)
Θέματα Εξετάσεων Μαθηματικών Κατεύθυνσης ΓΛ 2000-10 σε word (Ημερησίων, Εσπερινών, Προαγωγικών, Επαναληπτικών)
Θέματα Εξετάσεων Μαθηματικών Ομογενών ΓΛ 2001-10 σε pdf (τα υπόλοιπα υπάρχουν στο site της ΟΕΦΕ)

Μην δημοσιεύετε ασκήσεις σε αυτό το αρχείο, εδώ θα περνάω μόνο τα links από άλλες δημοσιεύσεις.
Περιμένω τα σχόλια σας και την κριτική σας καθώς και προτάσεις πως μπορεί να βελτιωθεί το παρόν bulletin.
Τα κόκκινα γράμματα υποδηλώνουν ότι οι ασκήσεις είναι άλυτες.

Αγαπητέ συνάδελφε, ΧΙΛΙΑ ΕΥΧΑΡΙΣΤΩ για την υπέροχη δουλειά που μας προσφέρεις.

wavelet

Πολύ καλή δουλεία

Κώστας Μαλλιάκας

Συγχαρητήρια για την δουλειά σου και τον κόπο σου που δεν πάει χαμένος αλλά και στην ιδέα σου για αυτό το νοικοκύρεμα ...

Ellas95

Ευχαριστουμε!Πολη καλη δουλεια!

Bulletin Επανάληψη ΓΛ ΣΥΝΑΡΤ. ΟΡΙΑ ΣΥΝΕΧΕΙΑ

Bulletin Επανάληψη ΓΛ ΣΥΝΑΡΤ. ΟΡΙΑ ΣΥΝΕΧΕΙΑ

Re: Bulletin Επανάληψης ΓΛ ΣΥΝΑΡΤΗΣΕΙΣ ΟΡΙΑ ΣΥΝΕΧΕΙΑ

Re: Bulletin Επανάληψης ΓΛ ΣΥΝΑΡΤΗΣΕΙΣ ΟΡΙΑ ΣΥΝΕΧΕΙΑ

Re: Bulletin Επανάληψης ΓΛ ΣΥΝΑΡΤΗΣΕΙΣ ΟΡΙΑ ΣΥΝΕΧΕΙΑ

Re: Bulletin Επανάληψης ΓΛ ΣΥΝΑΡΤΗΣΕΙΣ ΟΡΙΑ ΣΥΝΕΧΕΙΑ

Μέλη σε σύνδεση