Να προσδιορίσετε τους ακεραίους
 για τους οποίους ισχύει
για τους οποίους ισχύει  .
.Θέμα 2ο
Σε οξυγώνιο τρίγωνο
 φέρνουμε τα ύψη
φέρνουμε τα ύψη  . Αν η
. Αν η  είναι παράλληλη στην
είναι παράλληλη στην  , η γωνία
, η γωνία  είναι
είναι  και
και  να προσδιορίσετε τα μέτρα των πλευρών και των γωνιών του τριγώνου
να προσδιορίσετε τα μέτρα των πλευρών και των γωνιών του τριγώνου  .
.Θέμα 3ο
Για οποιουσδήποτε θετικούς αριθμούς
 να αποδείξετε ότι το κλάσμα
να αποδείξετε ότι το κλάσμα  βρίσκεται μεταξύ των αριθμών
βρίσκεται μεταξύ των αριθμών  . (Τα
. (Τα  είναι τέτοια ώστε να έχουν έννοια τα παραπάνω κλάσματα).
είναι τέτοια ώστε να έχουν έννοια τα παραπάνω κλάσματα).Θέμα 4ο
Θεωρούμε μία τριγωνική τοποθέτηση των αριθμών
 . Οι αριθμοί που βρίσκονται στο εσωτερικό του τριγώνου είναι ίσοι με το άθροισμα των δύο γειτονικών αριθμών της προηγούμενης σειράς. Για παράδειγμα οι έξι πρώτες σειρές είναι:
. Οι αριθμοί που βρίσκονται στο εσωτερικό του τριγώνου είναι ίσοι με το άθροισμα των δύο γειτονικών αριθμών της προηγούμενης σειράς. Για παράδειγμα οι έξι πρώτες σειρές είναι:
Έστω
 το άθροισμα των αριθμών της
το άθροισμα των αριθμών της  σειράς. Να προσδιορίσετε τα δύο τελευταία ψηφία του
σειράς. Να προσδιορίσετε τα δύο τελευταία ψηφία του  .
.Αλέξανδρος

 ,
, .
. , το τετράπλευρο
, το τετράπλευρο  θα είναι εγγράψιμο σε κύκλο διαμέτρου
θα είναι εγγράψιμο σε κύκλο διαμέτρου  . Άρα, θα είναι
. Άρα, θα είναι 

 , οπότε το τρίγωνο
, οπότε το τρίγωνο  είναι ισόπλευρο και τα ύψη του
είναι ισόπλευρο και τα ύψη του  και
και  είναι και διάμεσοι. Άρα, θα είναι
είναι και διάμεσοι. Άρα, θα είναι 
 . Ο ισχυρισμός ισχύει για
. Ο ισχυρισμός ισχύει για  . Για το επαγωγικό βήμα αρκεί να δείξουμε ότι για κάθε
. Για το επαγωγικό βήμα αρκεί να δείξουμε ότι για κάθε  ισχύει ότι
ισχύει ότι  . Πράγματι αν ο ισχυρισμός ισχύει για
. Πράγματι αν ο ισχυρισμός ισχύει για  τότε θα ισχύει και για
τότε θα ισχύει και για  αφού τότε θα έχουμε
αφού τότε θα έχουμε  .
. . Αυτό είναι άμεσο αφού για να πάρουμε τους αριθμούς της
. Αυτό είναι άμεσο αφού για να πάρουμε τους αριθμούς της  σειράς προσθέτουμε τους αιρθμούς της
σειράς προσθέτουμε τους αιρθμούς της  και για αυτόν τον λόγο προκύπτει το
και για αυτόν τον λόγο προκύπτει το  στον τύπο.
στον τύπο. . Έχουμε
. Έχουμε  . Επίσης από Fermat-Euler, αφού
. Επίσης από Fermat-Euler, αφού  έχουμε
έχουμε  και άρα
και άρα  . Άρα
. Άρα  και
και  , δηλαδή τα δυο τελευταία ψηφία του
, δηλαδή τα δυο τελευταία ψηφία του 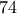 .
. Επομένως
Επομένως  . Τότε
. Τότε
 .
.
 είναι παρόμοια.
είναι παρόμοια.