parmenides51 έγραψε:4. Έστω

τέτοιο ώστε:
i) Αν

τότε

ii)

και

Να αποδειχτεί ότι :
![\displaystyle{\sqrt[\displaystyle2^{1453}]{2^{1821}}\in A} \displaystyle{\sqrt[\displaystyle2^{1453}]{2^{1821}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/f2e51c084cd232c3176748543c38dd97.png)

![\displaystyle{1\in A , \sqrt{2}\in A\Rightarrow \sqrtr{1.\sqrt{2}}\in A\Rightarrow \sqrt[2^2]{2}\in A} \displaystyle{1\in A , \sqrt{2}\in A\Rightarrow \sqrtr{1.\sqrt{2}}\in A\Rightarrow \sqrt[2^2]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/c021af5e35564b87b165d1c4409dfac7.png)
![\displaystyle{1\in A , \sqrt[2^2]{2}\in A\Rightarrow \sqrt{1.\sqrt[2^2]{2}}\in A\Rightarrow \sqrt[2^3]{2}\in A} \displaystyle{1\in A , \sqrt[2^2]{2}\in A\Rightarrow \sqrt{1.\sqrt[2^2]{2}}\in A\Rightarrow \sqrt[2^3]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/45e3194e6dccab24e1849539ed15848e.png)
Kαι εύκολα επαγωγικά, δείχνουμε ότι
![\displaystyle{\sqrt[2^n]{2}\in A} \displaystyle{\sqrt[2^n]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/a8be09758619c620ec461d6fe0d31350.png)
, (ΣΧΕΣΗ *), για κάθε
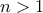
Επίσης, βλέπουμε ότι αν
![\displaystyle{\sqrt[2^n]{m}\in A \Rightarrow \sqrt{\sqrt[2^n]{m}.\sqrt[2^n]{m}}\in A \Rightarrow \sqrt[2^{n+1}]{m^2}\in A} \displaystyle{\sqrt[2^n]{m}\in A \Rightarrow \sqrt{\sqrt[2^n]{m}.\sqrt[2^n]{m}}\in A \Rightarrow \sqrt[2^{n+1}]{m^2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/5b025f2bbfa63040a535e37d4af859a0.png)
, (ΣΧΕΣΗ **), όπου

Θέτουμε τώρα στην σχέση (*)

. Tότε έχουμε
![\displaystyle{\sqrt[1437]{2}\in A} \displaystyle{\sqrt[1437]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/baab137137e522771cf3b27c3309a4f5.png)
. Oπότε από την σχέση (**), έχουμε:
![\displaystyle{\sqrt[2^{1438}]{2^2}\in A } \displaystyle{\sqrt[2^{1438}]{2^2}\in A }](/forum/ext/geomar/texintegr/latexrender/pictures/591157845648530acee8ebc4cfd8dd0a.png)
και εκ νέου από την (**) έχουμε
![\displaystyle{\sqrt[2^{1439}]{2^4}\in A} \displaystyle{\sqrt[2^{1439}]{2^4}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/a3567ffd000ada888969c343af1aa596.png)
και πάλι από την (**) συνεχίζοντας ομοίως, τελικά έχουμε:
![\displaystyle{\sqrt[2^{1447}]{2^{1024}}\in A} \displaystyle{\sqrt[2^{1447}]{2^{1024}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/b4935965c03f5c0c4b9b90e138c6b4a5.png)
, (1)
Για

, η σχέση (*) δίνει
![\displaystyle{\sqrt[2^{1438}]{2}\in A} \displaystyle{\sqrt[2^{1438}]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/7811b2f5f2237090679399aaf4b21d76.png)
και με βάση την (**), όπως και προηγουμένως, διαδοχικά θα πάρουμε ότι
![\displaystyle{\sqrt[2^{1447}]{2^{512}}\in A} \displaystyle{\sqrt[2^{1447}]{2^{512}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/11d217dfffe5666a1d391e7676426da9.png)
, (2)
Aπό τις (1) και (2) έχουμε ότι:
![\displaystyle{\sqrt{\sqrt[2^{1447}]{2^{1024}}.\sqrt[2^{1447}]{2^{512}}\in A} \displaystyle{\sqrt{\sqrt[2^{1447}]{2^{1024}}.\sqrt[2^{1447}]{2^{512}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/114129b5e5907803dfb4a65922436e67.png)
. Δηλαδή:
![\displaystyle{\sqrt[2^{1448}]{2^{1536}}\in A} \displaystyle{\sqrt[2^{1448}]{2^{1536}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/47a624afff6d770596ee5b3c5f875364.png)
, (3)
Συνεχίζοντας, θέτουμε στην (*),

και εργαζόμενοι με τα ίδια όπως πριν βήματα, βρίσκουμε ότι :
![\displaystyle{\sqrt[2^{1448}]{2^{256}}\in A} \displaystyle{\sqrt[2^{1448}]{2^{256}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/2f0c5f45705b3c1fe4aabb0ee9b90729.png)
, (4)
Από τις σχέσεις (3) , (4) παίρνουμε:
![\displaystyle{\sqrt[2^{1449}]{2^{1792}}\in A} \displaystyle{\sqrt[2^{1449}]{2^{1792}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/aebdfce101e4a5da26cf0742d463c234.png)
, (5)
Θέτουμε στην (*) ,

, οπότε βρίσκουμε ότι
![\displaystyle{\sqrt[2^{1449}]{2^{16}}\in A} \displaystyle{\sqrt[2^{1449}]{2^{16}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/775d4d0ab3d41a49dd69c227ad400292.png)
, (6)
Aπό (5) , (6) έχουμε:
![\displaystyle{\sqrt[2^{1450}]{2^{1808}}\in A} \displaystyle{\sqrt[2^{1450}]{2^{1808}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/f0f58a6a1ffec346afdf6c214571a5a4.png)
, (7)
Θέτουμε στην (*) ,

. Tότε βρίσκουμε
![\displaystyle{\sqrt[2^{1450}]{2^8}\in A} \displaystyle{\sqrt[2^{1450}]{2^8}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/c3477781827affd4dee69d0af5765f21.png)
, (8)
Από (7) , (8) έχουμε:
![\displaystyle{\sqrt[2^{1451}]{2^{1816}}\in A} \displaystyle{\sqrt[2^{1451}]{2^{1816}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/a989c9cf30db5f111c9cd1c9a374f5b5.png)
,(9)
Θέτουμε στην (*) ,

. Τότε βρίσκουμε
![\displaystyle{\sqrt[2^{1451}]{2^4}\in A} \displaystyle{\sqrt[2^{1451}]{2^4}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/a575379886d2f113820338e3b4059abc.png)
, (10)
Από (9),(10) έχουμε:
![\displaystyle{\sqrt[2^{1452}]{2^{1820}}\in A} \displaystyle{\sqrt[2^{1452}]{2^{1820}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/7e3432b625f29c4c612b58b97b688a5d.png)
, (11)
Tέλος, θέτουμε στην (*) ,

. Τότε
![\displaystyle{\sqrt[2^{1452}]{2}\in A} \displaystyle{\sqrt[2^{1452}]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/df66f372e2260c2a5faf6ca21bb475bc.png)
, (12)
Από (11) , (12) βρίσκουμε:
![\displaystyle{\sqrt[2^{1453}]{2^{1821}}\in A} \displaystyle{\sqrt[2^{1453}]{2^{1821}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/19d8da97c72bcec1929f03be6abbc7aa.png)
, όπως θέλαμε.
ΣΗΜ: Δεν μπόρεσα να σκεφτώ ευκολώτερη λύση. Αν κάποιος καταφέρει κάτι πιο απλό, ας το δημοσιεύσει
 και
και 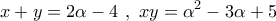 .
. ;
; εγγεγραμμένο σε κύκλου
εγγεγραμμένο σε κύκλου 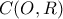 . Αν
. Αν  είναι σημείο του τόξου
είναι σημείο του τόξου  και αν
και αν  είναι οι πόδες των καθέτων που άγονται από το σημείο
είναι οι πόδες των καθέτων που άγονται από το σημείο  επί των ευθειών
επί των ευθειών 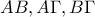 αντίστοιχα.
αντίστοιχα. όπου
όπου  το ύψος που αντιστοιχεί στην πλευρά
το ύψος που αντιστοιχεί στην πλευρά  .
. και
και  σ' έαν ορθογώνιο παραλληλόγραμμο
σ' έαν ορθογώνιο παραλληλόγραμμο  τέμνουν τις πλευρές
τέμνουν τις πλευρές  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα.
αντίστοιχα. 
 τέτοιο ώστε:
τέτοιο ώστε: τότε
τότε 
 και
και 
![\displaystyle{\sqrt[\displaystyle2^{1453}]{2^{1821}}\in A} \displaystyle{\sqrt[\displaystyle2^{1453}]{2^{1821}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/f2e51c084cd232c3176748543c38dd97.png)


 (1)
(1) ώστε να ισχύουν οι παραπάνω σχέσεις πρέπει να υπάρχει
ώστε να ισχύουν οι παραπάνω σχέσεις πρέπει να υπάρχει 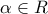 ώστε η εξίσωση
ώστε η εξίσωση  , όπου
, όπου  και
και  , να έχει πραγματικές ρίζες, δηλαδή πρέπει:
, να έχει πραγματικές ρίζες, δηλαδή πρέπει: 
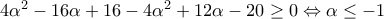
 παρουσιάζει ελάχιστο αν
παρουσιάζει ελάχιστο αν 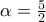 δηλαδή στο διάστημα
δηλαδή στο διάστημα 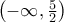 είναι γν. φθίνουσα, έτσι και στο διάστημα
είναι γν. φθίνουσα, έτσι και στο διάστημα ![\left( -\infty ,-1 \right] \left( -\infty ,-1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/d378ca0947d9cf092b66ef2026df24f6.png) είναι γν. φθίνουσα.
είναι γν. φθίνουσα. παρουσιάζει ελάχιστο αν
παρουσιάζει ελάχιστο αν  , το
, το 

 αντίστοιχα έχουμε:
αντίστοιχα έχουμε:  . Με πρόσθεση κατά μέλη και από την τριγωνική ανισότητα παίρνουμε:
. Με πρόσθεση κατά μέλη και από την τριγωνική ανισότητα παίρνουμε:  .
.
![\displaystyle{1\in A , \sqrt{2}\in A\Rightarrow \sqrtr{1.\sqrt{2}}\in A\Rightarrow \sqrt[2^2]{2}\in A} \displaystyle{1\in A , \sqrt{2}\in A\Rightarrow \sqrtr{1.\sqrt{2}}\in A\Rightarrow \sqrt[2^2]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/c021af5e35564b87b165d1c4409dfac7.png)
![\displaystyle{1\in A , \sqrt[2^2]{2}\in A\Rightarrow \sqrt{1.\sqrt[2^2]{2}}\in A\Rightarrow \sqrt[2^3]{2}\in A} \displaystyle{1\in A , \sqrt[2^2]{2}\in A\Rightarrow \sqrt{1.\sqrt[2^2]{2}}\in A\Rightarrow \sqrt[2^3]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/45e3194e6dccab24e1849539ed15848e.png)
![\displaystyle{\sqrt[2^n]{2}\in A} \displaystyle{\sqrt[2^n]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/a8be09758619c620ec461d6fe0d31350.png) , (ΣΧΕΣΗ *), για κάθε
, (ΣΧΕΣΗ *), για κάθε 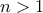
![\displaystyle{\sqrt[2^n]{m}\in A \Rightarrow \sqrt{\sqrt[2^n]{m}.\sqrt[2^n]{m}}\in A \Rightarrow \sqrt[2^{n+1}]{m^2}\in A} \displaystyle{\sqrt[2^n]{m}\in A \Rightarrow \sqrt{\sqrt[2^n]{m}.\sqrt[2^n]{m}}\in A \Rightarrow \sqrt[2^{n+1}]{m^2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/5b025f2bbfa63040a535e37d4af859a0.png) , (ΣΧΕΣΗ **), όπου
, (ΣΧΕΣΗ **), όπου 
 . Tότε έχουμε
. Tότε έχουμε ![\displaystyle{\sqrt[1437]{2}\in A} \displaystyle{\sqrt[1437]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/baab137137e522771cf3b27c3309a4f5.png) . Oπότε από την σχέση (**), έχουμε:
. Oπότε από την σχέση (**), έχουμε:![\displaystyle{\sqrt[2^{1438}]{2^2}\in A } \displaystyle{\sqrt[2^{1438}]{2^2}\in A }](/forum/ext/geomar/texintegr/latexrender/pictures/591157845648530acee8ebc4cfd8dd0a.png) και εκ νέου από την (**) έχουμε
και εκ νέου από την (**) έχουμε ![\displaystyle{\sqrt[2^{1439}]{2^4}\in A} \displaystyle{\sqrt[2^{1439}]{2^4}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/a3567ffd000ada888969c343af1aa596.png)
![\displaystyle{\sqrt[2^{1447}]{2^{1024}}\in A} \displaystyle{\sqrt[2^{1447}]{2^{1024}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/b4935965c03f5c0c4b9b90e138c6b4a5.png) , (1)
, (1) , η σχέση (*) δίνει
, η σχέση (*) δίνει ![\displaystyle{\sqrt[2^{1438}]{2}\in A} \displaystyle{\sqrt[2^{1438}]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/7811b2f5f2237090679399aaf4b21d76.png) και με βάση την (**), όπως και προηγουμένως, διαδοχικά θα πάρουμε ότι
και με βάση την (**), όπως και προηγουμένως, διαδοχικά θα πάρουμε ότι ![\displaystyle{\sqrt[2^{1447}]{2^{512}}\in A} \displaystyle{\sqrt[2^{1447}]{2^{512}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/11d217dfffe5666a1d391e7676426da9.png) , (2)
, (2)![\displaystyle{\sqrt{\sqrt[2^{1447}]{2^{1024}}.\sqrt[2^{1447}]{2^{512}}\in A} \displaystyle{\sqrt{\sqrt[2^{1447}]{2^{1024}}.\sqrt[2^{1447}]{2^{512}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/114129b5e5907803dfb4a65922436e67.png) . Δηλαδή:
. Δηλαδή:![\displaystyle{\sqrt[2^{1448}]{2^{1536}}\in A} \displaystyle{\sqrt[2^{1448}]{2^{1536}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/47a624afff6d770596ee5b3c5f875364.png) , (3)
, (3) και εργαζόμενοι με τα ίδια όπως πριν βήματα, βρίσκουμε ότι :
και εργαζόμενοι με τα ίδια όπως πριν βήματα, βρίσκουμε ότι :![\displaystyle{\sqrt[2^{1448}]{2^{256}}\in A} \displaystyle{\sqrt[2^{1448}]{2^{256}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/2f0c5f45705b3c1fe4aabb0ee9b90729.png) , (4)
, (4)![\displaystyle{\sqrt[2^{1449}]{2^{1792}}\in A} \displaystyle{\sqrt[2^{1449}]{2^{1792}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/aebdfce101e4a5da26cf0742d463c234.png) , (5)
, (5) , οπότε βρίσκουμε ότι
, οπότε βρίσκουμε ότι ![\displaystyle{\sqrt[2^{1449}]{2^{16}}\in A} \displaystyle{\sqrt[2^{1449}]{2^{16}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/775d4d0ab3d41a49dd69c227ad400292.png) , (6)
, (6)![\displaystyle{\sqrt[2^{1450}]{2^{1808}}\in A} \displaystyle{\sqrt[2^{1450}]{2^{1808}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/f0f58a6a1ffec346afdf6c214571a5a4.png) , (7)
, (7) . Tότε βρίσκουμε
. Tότε βρίσκουμε ![\displaystyle{\sqrt[2^{1450}]{2^8}\in A} \displaystyle{\sqrt[2^{1450}]{2^8}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/c3477781827affd4dee69d0af5765f21.png) , (8)
, (8)![\displaystyle{\sqrt[2^{1451}]{2^{1816}}\in A} \displaystyle{\sqrt[2^{1451}]{2^{1816}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/a989c9cf30db5f111c9cd1c9a374f5b5.png) ,(9)
,(9)  . Τότε βρίσκουμε
. Τότε βρίσκουμε ![\displaystyle{\sqrt[2^{1451}]{2^4}\in A} \displaystyle{\sqrt[2^{1451}]{2^4}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/a575379886d2f113820338e3b4059abc.png) , (10)
, (10)![\displaystyle{\sqrt[2^{1452}]{2^{1820}}\in A} \displaystyle{\sqrt[2^{1452}]{2^{1820}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/7e3432b625f29c4c612b58b97b688a5d.png) , (11)
, (11) . Τότε
. Τότε ![\displaystyle{\sqrt[2^{1452}]{2}\in A} \displaystyle{\sqrt[2^{1452}]{2}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/df66f372e2260c2a5faf6ca21bb475bc.png) , (12)
, (12)![\displaystyle{\sqrt[2^{1453}]{2^{1821}}\in A} \displaystyle{\sqrt[2^{1453}]{2^{1821}}\in A}](/forum/ext/geomar/texintegr/latexrender/pictures/19d8da97c72bcec1929f03be6abbc7aa.png) , όπως θέλαμε.
, όπως θέλαμε.
 , όπου
, όπου 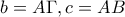
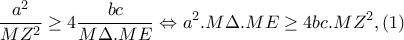
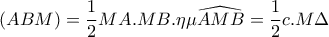
 , έχω:
, έχω: 
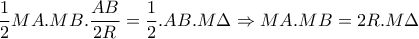 , (2)
, (2) , (3)
, (3)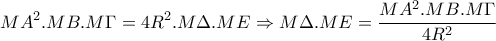 ,(4)
,(4)
 , 'εχουμε:
, 'εχουμε:
 , (5)
, (5)
 , (6)
, (6) , έχουμε:
, έχουμε: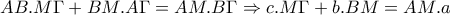
 , η οποία προφανώς είναι αληθής.
, η οποία προφανώς είναι αληθής.