gbaloglou έγραψε:....
Πιστεύω επίσης ότι αν ο ισχυρισμός αποδειχθεί τελικά αληθής ... θα πρόκειται για ΠΑΝΕΜΟΡΦΟ αποτέλεσμα!
Ωραίο θα είναι, πράγματι.
Αν είχαμε μια καλή βιβλιογραφία στη διάθεσή μας θα μπορούσαμε να το ψάξουμε. Ένα άλλο αποτέλεσμα του κ. Κωνσταντόπουλου έπεται από μια άσκηση που βρήκα στο "Mathematical Analysis" του Apostol για παράδειγμα.
Δεν είμαι σίγουρος, όμως, ότι ο ισχυρισμός έχει διατυπωθεί σωστά.
Τι σημαίνει "
το σημείο ξ του Θ.Μ.Τ. του διαφορικού" και "
το σημείο ξ του ...";
Για οποιαδήποτε από τα δύο θεωρήματα μέσης τιμής, τα σημεία αυτά δεν είναι κατ'ανάγκη μοναδικά.
Ποια εκδοχή από τις παρακάτω είναι η σωστή;
**********************************************************
ΕΚΔΟΧΗ 1. Αν η παραγωγίσιμη συνάρτηση

είναι τέτοια ώστε, για κάθε
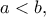
υπάρχει
μοναδικό 
τέτοιο ώστε

και

,
τότε ισχύει

για κάθε

(με

σταθερές).
**********************************************************
ή
**********************************************************
ΕΚΔΟΧΗ 2. Αν η παραγωγίσιμη συνάρτηση

είναι τέτοια ώστε, για κάθε
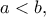
υπάρχει

τέτοιο ώστε

και

,
τότε ισχύει

για κάθε

(με

σταθερές).
**********************************************************
Rafaelcrete έγραψε:....
ΙΣΧΥΡΙΣΜΟΣ
Δεν υπάρχει άλλη στοιχειώδης συνάρτηση με την παραπάνω ιδιότητα.
Σε καμιά από τις παραπάνω εκδοχές δεν υπάρχει η λέξη "στοιχειώδης", όμως. Πως θα μπορούσε να συμπεριληφθεί και τι σημαίνει ακριβώς;
Θα πρέπει ο ισχυρισμός να διατυπωθεί με περισσότερη σαφήνεια.
Φιλικά,
Αχιλλέας
 όπου
όπου  τυχαία σταθερά και
τυχαία σταθερά και  και σε κάθε διάστημα,το σημείο
και σε κάθε διάστημα,το σημείο  του Θ.Μ.Τ. του διαφορικού λογισμού και το σημείο
του Θ.Μ.Τ. του διαφορικού λογισμού και το σημείο  του Θ.Μ.Τ. του ολοκληρωτικού λογισμού,ταυτίζονται.
του Θ.Μ.Τ. του ολοκληρωτικού λογισμού,ταυτίζονται.
 βρίσκω ότι
βρίσκω ότι 

 για όλα τα
για όλα τα  τότε θέτοντας
τότε θέτοντας  βρίσκω
βρίσκω  . Δηλαδή
. Δηλαδή  για όλα τα
για όλα τα  . και επομένως θέτοντας
. και επομένως θέτοντας  .
.  .
.  είναι τέτοια ώστε, για κάθε
είναι τέτοια ώστε, για κάθε 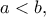 υπάρχει μοναδικό
υπάρχει μοναδικό  τέτοιο ώστε
τέτοιο ώστε και
και  ,
,  για κάθε
για κάθε  (με
(με  σταθερές).
σταθερές).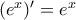 και αρκετά αργότερα ότι αυτή είναι η μοναδική συνάρτηση με αυτή την ιδιότητα.
και αρκετά αργότερα ότι αυτή είναι η μοναδική συνάρτηση με αυτή την ιδιότητα.
 , το
, το  ικανοποιεί και τα δύο αποτελέσματα:
ικανοποιεί και τα δύο αποτελέσματα: και
και  .
. με γνησίως μονότονη παράγωγο για τις οποίες για κάθε
με γνησίως μονότονη παράγωγο για τις οποίες για κάθε  και
και 
 με
με  .
.