Μαθηματικοί διαγωνισμοί - Γυμνάσιο

#1161

socrates έγραψε:ΑΣΚΗΣΗ 551
Αν η εξίσωση έχει ακέραια ρίζα να δείξετε ότι $\displaystyle{\frac{1}{2}<\frac{m}{n}<2.}$

Καλησπέρα. Τα m , n

είναι ακέραιοι;

#1162

ΔΗΜΗΤΡΗΣ έγραψε:
socrates έγραψε:ΑΣΚΗΣΗ 551
Αν η εξίσωση έχει ακέραια ρίζα να δείξετε ότι $\displaystyle{\frac{1}{2}<\frac{m}{n}<2.}$
Καλησπέρα. Τα είναι ακέραιοι;

Θετικοί ακέραιοι!!

#1163

socrates έγραψε:ΑΣΚΗΣΗ 553
Να βρεθούν οι ρητοί αν $\sqrt{x\sqrt{5}}-\sqrt{y\sqrt{5}}=\sqrt{6\sqrt{5}-10}.$

Αρχικά, πρέπει $\displaystyle{\sqrt{x\sqrt{5}}-\sqrt{y\sqrt{5}}\geq 0\Leftrightarrow x\geq y}$

Τώρα, η δοσμένη σχέση, γράφεται:

$\displaystyle{\sqrt{x\sqrt{5}}=\sqrt{6\sqrt{5}-10}+\sqrt{y\sqrt{5}}\Leftrightarrow }$ ,(με ύψωση στο τετράγωνο)

$\displaystyle{x\sqrt{5}=6\sqrt{5}-10+y\sqrt{5}+2\sqrt{y\sqrt{5}(6\sqrt{5}-10)}\Leftrightarrow}$

$\displaystyle{(x-y-6)\sqrt{5}+10=2\sqrt{y(30-10\sqrt{5})}}$

Με νέα ύψωση στο τετράγωνο, έχουμε:

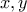$\displaystyle{(x-y-6)^{2}.5+100-120y=[-20(x-y-6)-40y]\sqrt{5}}$ . Και αφού οι $\displaystyle{x , y}$ είναι ρητοί, θα πρέπει:

$\displaystyle{5.(x-y-6)^{2}+100-120y=0}$

$\displaystyle{20(x-y-6)+40y=0}$

Άρα:

$\displaystyle{y^{2}-6y+5=0}$

$\displaystyle{x=6-y}$

Και αφού $\displaystyle{x\geq y}$ , προκύπτει η μοναδική λύση $\displaystyle{x=5 , y=1}$ , η οποία επαληθεύει την δοσμένη εξίσωση.

#1164

socrates έγραψε:ΑΣΚΗΣΗ 551
Αν η εξίσωση έχει ακέραια ρίζα να δείξετε ότι $\displaystyle{\frac{1}{2}<\frac{m}{n}<2.}$

ΔΗΜΗΤΡΗΣ έγραψε:Τα είναι ακέραιοι;

socrates έγραψε:Θετικοί ακέραιοι!!

Λόγω συμμετρίας της δοσμένης εξίσωσης υποθέτουμε ότι $m\geq n$ .

Τότε $\dfrac{m}{n} \geq 1>\dfrac{1}{2}$ . Επίσης η εξίσωση γράφεται: $(x+m)(x+n)=(x+m)+n \Longleftrightarrow (x+m)(x+n-1)=n$ . Τότε όμως οι δύο παράγοντες του γινομένου είναι ακέραιοι αριθμοί και διαιρέτες του

. Συνεπώς η διαφορά τους είναι μικρότερη ή ίση από n-1

.

Άρα $(x+m)-(x+n-1)\leq n-1$ δηλαδή $m\leq 2n-2$ δηλαδή $\dfrac{m}{n}\leq 2-\dfrac{2}{n}$

Οπότε τελικά $\dfrac{1}{2}<\dfrac{m}{n} \leq 2-\dfrac{2}{n} < 2$ που θέλαμε.

Όμοια αν $n\geq m$ τότε αφενός $\dfrac{m}{n}\leq 1<2$ και αφετέρου αν γράψουμε την αρχική εξίσωση ως (x+m-1)(x+n)=m

τότε (όμοια όπως πριν) πρέπει $x+n-(x+m-1) \leq m-1$ οπότε $n\leq 2m-2$ δηλαδή $\dfrac{m}{n}\geq \dfrac{1}{2}+\dfrac{1}{n}$

Άρα τελικά και σε αυτή την περίπτωση έχουμε: $\dfrac{1}{2}< \dfrac{1}{2}+\dfrac{1}{n} \leq \dfrac{m}{n} < 2$

Αλέξανδρος

#1165

ΑΣΚΗΣΗ 554
Να λυθεί το σύστημα

$\displaystyle{\begin{cases} \sqrt{x-y^2}=z-1 \\ \sqrt{y-z^2}=x-1 \\ \sqrt{z-x^2}=y-1 \end{cases}}$

ΑΣΚΗΣΗ 555
Να λυθεί το σύστημα

$\displaystyle{\begin{cases} \sqrt{x^2-y}=z-1 \\ \sqrt{y^2-z}=x-1 \\ \sqrt{z^2-x}=y-1 \end{cases}}$

ΑΣΚΗΣΗ 556
Ένα ημικυκλικό κομμάτι χαρτί, ακτίνας 10, διπλώνεται ώστε να σχηματιστεί κώνος.
Να βρεθεί το ύψος του.

ΑΣΚΗΣΗ 557
Οι πρώτοι αριθμοί p,q

είναι τέτοιοι ώστε $q \mid p^2+1$ και $p \mid q^2-1$ .

Δείξτε ότι ο αριθμός p+q+1

είναι σύνθετος.

Atemlos · #1166

Ασκηση 556)

Έστω

η ακτίνα του κώνου και

η ακτίνα του κύκλου . Τότε $R= \frac{r}{2}$ και το ύψος

$h= \sqrt{r^2-R^2} \Rightarrow h= \frac{ \sqrt{3} }{2} r$

kostas136 · #1167

Για την 554.
Λόγω των περιορισμών θα πρέπει να ισχύει:

$\displaystyle z\geq 1\ ,\ x\geq 1\ ,\ y\geq 1\ ,\ x\geq y^2\ ,\ y\geq z^2\ ,\ z\geq x^2$

$\displaystyle z\geq x^2\Rightarrow z\geq y^4\Rightarrow z\geq z^8\Rightarrow z^7\leq 1$

Αλλά:

$\displaystyle z^7\geq 1\Rightarrow z^7=1\Rightarrow z=1$

Ομοίως: $\displaystyle x=y=z=1$

dr.tasos · #1168

socrates έγραψε:ΑΣΚΗΣΗ 554
Να λυθεί το σύστημα

$\displaystyle{\begin{cases} \sqrt{x-y^2}=z-1 \\ \sqrt{y-z^2}=x-1 \\ \sqrt{z-x^2}=y-1 \end{cases}}$

Πρέπει να είναι αρχικά $\displaystyle{ x,y,z \geq 1 }$

Τετραγωνίζω ολες τις σχέσεις και προσθέτω και έχω

$x+y+z-(x^2+y^2+z^2)=x^2+y^2+z^2+3-2(x+y+z) \Leftrightarrow 3 (x+y+z)-3=2(x^2+y^2+z^2) \Leftrightarrow x^2-2x+1+y^2-2y+1+z^2-2z+1+x^2-x+y^2-y+z^2-z=0 \Leftrightarrow (x-1)^2+(y-1)^2+(z-1)^2+x(x-1)+y(y-1)+z(z-1)=0$

ολοι οι όροι ειναι μη αρνητικοι ακομα και οι $\displaystyle{ x(x-1),y(y-1),z(z-1) }$

Λογω του αρχικου περιορισμου οτι $\displaystyle{ x,z,y \geq 1 }$

έτσι είναι $\displaystyle{ x=y=z=1 }$

kostas136 · #1169

Για την 555:

Λόγω περιορισμών θα ισχύει:

$\displaystyle x\geq 1\ ,\ y\geq 1\ ,\ z\geq 1$

Τετραγωνίζοντας και προσθέτοντας κατά μέλη προκύπτει:

$\displaystyle x^2-y+y^2-z+z^2-x=(z-1)^2+(x-1)^2+(y-1)^2\Rightarrow x+y+z=3$

Αλλά: $\displaystyle x+y+z\geq 3$ με το ελάχιστο να "πιάνεται" αν και μόνο αν $\displaystyle x=y=z=1$

dr.tasos · #1170

socrates έγραψε: ΑΣΚΗΣΗ 555
Να λυθεί το σύστημα

$\displaystyle{\begin{cases} \sqrt{x^2-y}=z-1 \\ \sqrt{y^2-z}=x-1 \\ \sqrt{z^2-x}=y-1 \end{cases}}$

Πρέπει $\displaystyle{ x,y,z \geq 1 }$ κλασσικα λογω ριζικου κτλ .

Τετραγωνιζω προσθέτω κατα μέλη και έχω:

$\displaystyle{ (x^2+y^2+z^2)-(x+y+z)=(x^2+y^2+z^2)+3-2(z+x+y) \Leftrightarrow x+y+z=3 }$

Θέλω όμως $\displaystyle{ z \geq 1 \Leftrightarrow 3-x-y \geq 1 \Leftrightarrow -x-y \geq -2 \Leftrightarrow x+y \leq 2 }$

Αφου όμως $\displaystyle{ x \geq 1 \wedge y \geq 1 \Rightarrow x+y \geq 2 }$ Συνεπως θα ισχυει η ισότητα άρα
αν καποιος απο τους $\displaystyle{ x,y }$ ηταν μεγαλυτερος απο $\displaystyle{ 1 }$ τοτε το αθροισμα τους θα ηταν μεγαλυτερο απο 2 συνεπως παιρνουμε ατοπο και ισχυει $\displaystyle{ x=y=1 }$ άρα και $\displaystyle{ z=1 }$

dr.tasos · #1171

Νταξ μας εφαγε λαχανο ο κυριος Κωστας .

Να προσθεσω οτι την 555 μπορουμε να την τελειώσουμε προσθετοντας ολες τις σχεσεις κατα μελη και βγάζω εύκολα

$\displaystyle{ x^2=y \wedge y^2=z \wedge z^2=x }$
Συνδιαζοντας τις παραπανω παίρνω $\displaystyle{ y^4=x }$

Και επειτα $\displaystyle{ y^8=y \Rightarrow y=1 }$ αφου $\displaystyle{ y \geq 1 }$ εύκολα θα πάρω $\displaystyle{ x=y=z=1 }$ .

Αρχιμήδης 6 · #1172

Για την άσκηση 557 θεωρώ πως το καλύτερο θα ήταν να βρεθούν όλες οι ακέραιες λύσεις..

#1173

socrates έγραψε: ΑΣΚΗΣΗ 557
Οι πρώτοι αριθμοί είναι τέτοιοι ώστε $q \mid p^2+1$ και $p \mid q^2-1$ .

Δείξτε ότι ο αριθμός είναι σύνθετος.

Λύση αφιερωμένη στους μαθητές του 6ου καλοκαιρινού μαθηματικού σχολείου στη Βέροια:

Έχουμε τις περιπτώσεις:

Αν p=2

, τότε

, αφού $q \mid p^2+1=5$ , οπότε p+q+1=8

, κι άρα είναι σύνθετος.

Αν q=2

, τότε

, αφού $p \mid q^2-1=3$ , οπότε p+q+1=6

, κι άρα είναι σύνθετος.

Ας υποθέσουμε, λοιπόν, ότι p>2

και

. Τότε, αφού $p \mid q^2-1=(q-1)(q+1)$ , θα είναι $p \mid q+1$ ή $p \mid q-1$ .

Αλλά, δε μπορεί να ισχύει $p \mid q-1$ . [Διότι τότε για τον θετικό ακέραιο $k=\dfrac{p^2+1}{q}$ θα είναι

$p \mid k(q-1)=p^2-(k-1)$ , κι άρα $p \mid k-1$ , αλλά

$k=\dfrac{p^2+1}{q}\leq \dfrac{p^2+1}{p+1}<p$ , αφού $p\leq q-1$ .

Συνεπώς, αφού k<p

και $p\mid k-1$ έπεται ότι k=1

, οπότε θα είναι q=p^2+1

, δηλ. περιττός=άρτιος, άτοπο].

Άρα $p\mid q+1$ , οπότε ο p+q+1

, που είναι μεγαλύτερος από τον

, είναι σύνθετος ως πολλαπλάσιο του

.

Φιλικά,

Αχιλλέας

Αρχιμήδης 6 · #1174

Άσκηση

εύρεση λύσεων...
Αν p/q+1

και

(2) τότε

άρα από

$p-1\leq q$ (4)

από

ισχύει $pq\leq p^2+q+1$ άρα
$q\leq\frac{p^2+1}{p-1}\leq p+2$ (5)

από

...

ή

και σαν λύσεις μετά από λίγες πράξεις θα βρούμε τις λύσεις (2,5),(3,2),(3,5)

Αυτές είναι όλες οι λύσεις.(Ευχαριστώ τον Αχιλλέα για την διόρθωση.

Φιλικά

Δημήτρης

#1175

Αρχιμήδης 6 έγραψε:Άσκηση εύρεση λύσεων...
Αν και (2) τότε
άρα από $p-1\leq q$
από ισχύει $pq\leqp+q^2+1$ άρα
$q\leq\frac{p^2+1}{p-1}\leq p+2$
από ...
ή ή ή και σαν λύσεις μετά από λίγες πράξεις θα βρούμε πάλι τις 2 λύσεις
Αυτές είναι όλες οι λύσεις.

Φιλικά

Δημήτρης

Η σχέση (2) δεν είναι σωστή.

Μια ακόμα λύση της 557 είναι p=3

και

.

Φιλικά,

Αχιλλέας

#1176

socrates έγραψε:ΑΣΚΗΣΗ 548
Να λυθεί το σύστημα

$\displaystyle{\begin{cases} x^2 - y = z^2 \\ y^2- z = x^2 \\ z^2- x = y^2 \end{cases}}$

Το δοσμένο σύστημα γράφεται:

x^2 -z^2 =y

Και με πρόσθεση ανά δύο των παραπάνω εξισώσεων, παίρνουμε:

(y-z)(y+z)=y+z

, ........................ΣΧΕΣΗ (1)

(x-y)(x+y)=x+y

, .......................ΣΧΕΣΗ (2)

(z-x)(z+x)=z+x

, .......................ΣΧΕΣΗ (3)

Αν ήταν $y+z\neq 0 , x+y\neq 0 , z+x\neq 0$ , τότε θα είχαμε:

y-z=1

που είναι αδύνατον, αφού με πρόσθεση κατά μέλη, παίρνουμε: 0=3

Άρα ένα τουλάχιστον από τα y+z , x+y , z+x

, θα είναι ίσο με μηδεν.

1η ΠΕΡΙΠΤΩΣΗ: y+z= 0

. Τότε

, και από την ΣΧΕΣΗ (3) έπεται: (x+y)(x-y)=-(x-y)

,.............ΣΧΕΣΗ (4)

Θα διακρίνουμε τώρα δύο υποπεριπτώσεις:

1(α) ΥΠΟΠΕΡΙΠΤΩΣΗ: x-y=0

, δηλαδή

. Tότε από την ΣΧΕΣΗ (2) έπεται ότι x=0

και άρα μια πρώτη λύση του συστήματος, είναι η (x,y,z)=(0,0,0)

1(b) ΥΠΟΠΕΡΙΠΤΩΣΗ: $x-y\neq 0$ , δηλαδή $x\neq y$ . Tότε από την ΣΧΕΣΗ (4) έπεται x+y=-1

και τώρα από την ΣΧΕΣΗ (2) έπεται ότι x-y=1

. Από τις δύο αυτές εξισώσεις, έχουμε x=0 , y=-1

και αφού

, παίρνουμε z=1

. Οπότε μια δεύτερη λύση του συστήματος, είναι η (x,y,z)=(0,-1,1)

2η ΠΕΡΙΠΤΩΣΗ: x+y=0

.

Τότε ομοίως με την 1η ΠΕΡΙΠΤΩΣΗ, βρίσκουμε επί πλέον την τρίτη λύση (x,y,z)=(-1,1,0)

3η ΠΕΡΙΠΤΩΣΗ: z+x=0

.

Τότε και πάλι εργαζόμενοι ομοίως, βρίσκουμε επί πλέον την τέταρτη λύση: (x,y,z)=(1,0,-1)

ΣΗΜ: Εύκολα επαληθεύουμε ότι οι τιμές των x,y,z

, που βρήκαμε, επαληθεύουν το αρικό μας σύστημα.

#1177

ΑΣΚΗΣΗ 558: Να αποδείξετε ότι:

Αν : $\displaystyle{1^2 + 2^2 +3^2 + . . . +50^2 =a}$ , τότε: $\displaystyle{1.2 + 2.3 + . . . +100.101 = 8a}$

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

#1178

ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 558: Να αποδείξετε ότι:

Αν : $\displaystyle{1^2 + 2^2 +3^2 + . . . +50^2 =a}$ , τότε: $\displaystyle{1.2 + 2.3 + . . . +100.101 = 8a}$

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ
Είναι προϊόν συζήτησης που είχαμε σε ταβερνάκι στους Ωρεούς της Εύβοιας, με τα μέλη μας: Μπάμπη Στεργίου, Φωτεινή Καλδή, Στάθη Κούτρα και gauss1988. Mε την ευκαιρία, να πω και ένα παράπονο: Θανάση (KARKAR), έμαθα ότι πέρασες από τα μέρη μας πριν λίγες μέρες. ΕΠΡΕΠΕ να επικοινωνούσες μαζί μας, να τα λέγαμε από κοντά!!!!!

Και μάλιστα ισχύει

$\displaystyle{\boxed{\sum_{k=1}^{2n}(k^2+k)=8\sum_{k=1}^{n}k^2}}$ ,

για κάθε θετικό ακέραιο $\displaystyle{n.}$

ΛΕΩΝΙΔΑΣ · #1179

ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 558: Να αποδείξετε ότι:

Αν : $\displaystyle{1^2 + 2^2 +3^2 + . . . +50^2 =a}$ , τότε: $\displaystyle{1.2 + 2.3 + . . . +100.101 = 8a}$

Η πρώτη σχέση γράφεται ως:
$(1^2 +50^2) + (2^2 + 49^2) + ... (25^2+26^2)= (51^2-2\times 1 \times 50) + (51^2-2\times 2\times 49) + ... + (51^2 -2\times 25 \times 26) = 25\times 51^2-2(1\times 50 + 2\times 49+...+ 25 \times 26)$
Για την δεύτερη τώρα χωρίζουμε τους όρους ανά δύο κατ'αυτόν τον τρόπο: $(1\times 2 + 2\times 3) + (3\times 4 + 4\times 5) + ...+ (99\times 100 +100\times 101)$
Παρατηρούμε ότι κάθε παρένθεση έχει τη μορφή n(n+1) + (n+1)(n+2)

. Μετά από πράξεις βλέπουμε ότι n(n+1)+(n+1)(n+2)=n^2+n+n^2+2n+n+2=2n^2+4n+2=2(n+1)^2

.
Άρα η δεύτερη σχέση γίνεται 2(2^2+4^2+...100^2)

. Δουλεύοντας με τον ίδιο τρόπο που δουλέψαμε στην πρώτη σχέση βλέπουμε ότι η παρένθεση ισούται με $25\times 102^2-2(2\times 100+4\times 98+...50\times 52) =4\times 25\times 51^2-2(4\times 1 \times 50+4\times 2\times 49+...+ 4\times 25\times 26)=4[25\times 51^2 -2(1\times 50 +2\times 49+...25\times 26)]=4a$
Τώρα πολλαπλασιάζοντας με το δυαράκι που αφήσαμε απ'έξω βλέπουμε ότι η δεύτερη σχέση ισούται τελικά με

.

#1180

socrates έγραψε:ΑΣΚΗΣΗ 546
Να λυθεί το σύστημα

$\displaystyle{\begin{cases} \sqrt{x^2+y^2}=z+1 \\ \sqrt{y^2+z^2}=x+1 \\ \sqrt{z^2+x^2}=y+1 \end{cases}}$

viewtopic.php?p=95276#p95276

Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Re: Μαθηματικοί διαγωνισμοί - Γυμνάσιο

Μέλη σε σύνδεση