Αν για τους θετικούς πραγματικούς αριθμούς
 ισχύει
ισχύει  , να αποδείξετε ότι:
, να αποδείξετε ότι: 
Πρόβλημα 2
Δίνονται δύο κύκλοι
 και
και  τέτοιοι, ώστε
τέτοιοι, ώστε  , και έστω
, και έστω  οι δύο κοινές εξωτερικές εφαπτομένες των κύκλων. Έστω
οι δύο κοινές εξωτερικές εφαπτομένες των κύκλων. Έστω  τα σημεία επαφής της
τα σημεία επαφής της  με τους κύκλους
με τους κύκλους  αντίστοιχα και
αντίστοιχα και  τα σημεία επαφής της
τα σημεία επαφής της  με τους κύκλους
με τους κύκλους  αντίστοιχα. Έστω επίσης
αντίστοιχα. Έστω επίσης  το μέσον του
το μέσον του  και
και  τα σημεία τομής των τμημάτων
τα σημεία τομής των τμημάτων  και
και  με τους κύκλους
με τους κύκλους  αντίστοιχα. Ονομάζουμε
αντίστοιχα. Ονομάζουμε  τα σημεία τομής της ευθείας
τα σημεία τομής της ευθείας  με τους κύκλους
με τους κύκλους  αντίστοιχα. Έστω ότι οι ευθείες
αντίστοιχα. Έστω ότι οι ευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  και οι εφαπτομένες των κύκλων στα σημεία
και οι εφαπτομένες των κύκλων στα σημεία  τέμνονται στο σημείο
τέμνονται στο σημείο  . Να αποδείξετε ότι οι κάθετες από τα σημεία
. Να αποδείξετε ότι οι κάθετες από τα σημεία  και
και  πάνω στα τμήματα
πάνω στα τμήματα  και
και  αντίστοιχα και η ευθεία
αντίστοιχα και η ευθεία  διέρχονται από το ίδιο σημείο.
διέρχονται από το ίδιο σημείο.Πρόβλημα 3
Να βρείτε όλα τα ζευγάρια των θετικών ακεραίων
 με
με  για τους οποίους ισχύουν ότι:
για τους οποίους ισχύουν ότι:(i) Ο αριθμός
 είναι θετικός ακέραιος και
είναι θετικός ακέραιος και (ii) Ο
 , όπου
, όπου  πρώτος και
πρώτος και  θετικός ακέραιος.
θετικός ακέραιος.Πρόβλημα 4
Δίνεται το σύνολο
 . Να βρείτε το μέγιστο πλήθος στοιχείων ενός υποσυνόλου
. Να βρείτε το μέγιστο πλήθος στοιχείων ενός υποσυνόλου  του
του  έτσι, ώστε για κάθε δύο στοιχεία
έτσι, ώστε για κάθε δύο στοιχεία  και
και 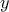 του
του  να έχουμε
να έχουμε  .
.Προσθέτω και τα θέματα



 με τουλάχιστον
με τουλάχιστον  στοιχεία. Τότε τουλάχιστον
στοιχεία. Τότε τουλάχιστον  από αυτά θα είναι στο
από αυτά θα είναι στο  . Άρα κάποιο από τα πέντε σύνολα
. Άρα κάποιο από τα πέντε σύνολα  ή
ή  ή ... ή
ή ... ή 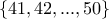 θα είχε τουλάχιστον
θα είχε τουλάχιστον  από τα στοιχεία του
από τα στοιχεία του  ). Χωρίς βλάβη το εν λόγω σύνολο είναι το
). Χωρίς βλάβη το εν λόγω σύνολο είναι το  . Όμως αυτό σίγουρα έχει δύο στοιχεία του
. Όμως αυτό σίγουρα έχει δύο στοιχεία του  είναι στο ίδιο από τα πέντε υποσύνολά του
είναι στο ίδιο από τα πέντε υποσύνολά του  ,
, ,
, ,
, ,
, . Άρα το
. Άρα το  ---(1)----
---(1)---- ----(2) ---οπότε μετά από αντικατάσταση του
----(2) ---οπότε μετά από αντικατάσταση του  στην πρώτη θα καταλήξω στην παρακάτω,
στην πρώτη θα καταλήξω στην παρακάτω, ---(3)---
---(3)--- τότε
τότε  ,
,  ,
, 
 τότε από ---(3)--- θα πρέπει
τότε από ---(3)--- θα πρέπει  ---(4)---
---(4)---
 είτε
είτε  είτε
είτε  και επειδή
και επειδή  αλλά από την ---(2)--- ισχύει ότι
αλλά από την ---(2)--- ισχύει ότι 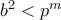 άρα
άρα  συνεπώς
συνεπώς  αδύνατον.
αδύνατον.
 αλλά δεν είναι δεκτή.
αλλά δεν είναι δεκτή.
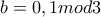 τότε δεν θα έχει λύσεις όπως έδειξα παραπάνω ενώ αν
τότε δεν θα έχει λύσεις όπως έδειξα παραπάνω ενώ αν  δεδομένου ότι τότε
δεδομένου ότι τότε  , η μέγιστη δύναμη του
, η μέγιστη δύναμη του  που διαιρεί τον
που διαιρεί τον  είναι
είναι  τότε,
τότε, άρα
άρα  αλλά από ---(2)---
αλλά από ---(2)--- άρα
άρα  οπότε μένει να ελέγξω
οπότε μένει να ελέγξω  (δεδομένου ότι
(δεδομένου ότι  άρα
άρα  οπότε από ---(2)---
οπότε από ---(2)--- 


 κτλ οπότε η υπόθεση γίνεται
κτλ οπότε η υπόθεση γίνεται  και το ζητούμενο
και το ζητούμενο 
 τότε το ζητούμενο είναι προφανές.
τότε το ζητούμενο είναι προφανές.  Από
Από  προκύπτει
προκύπτει  οπότε
οπότε 
 οπότε
οπότε 
 ή
ή  που ισχύει αφού
που ισχύει αφού  η τομή των καθέτων από τα
η τομή των καθέτων από τα  στις
στις  .
. δηλαδή το σημείο
δηλαδή το σημείο  άρα το
άρα το  είναι εγγράψιμο.Άρα
είναι εγγράψιμο.Άρα 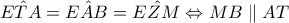 .Ομοίως
.Ομοίως  .
. .
. .
. είναι εγγράψιμο.Άρα
είναι εγγράψιμο.Άρα  δηλαδή το
δηλαδή το  .
. είναι ισοσκελές δηλαδή
είναι ισοσκελές δηλαδή  .Επομένως και το
.Επομένως και το  είναι συνευθειακά.Επίσης
είναι συνευθειακά.Επίσης  (ο ριζικός άξονας είναι κάθετος στη διάκεντρο).
(ο ριζικός άξονας είναι κάθετος στη διάκεντρο). και
και  το
το  .
. δηλαδή τα
δηλαδή τα  είναι συνευθειακά,δηλαδή τα
είναι συνευθειακά,δηλαδή τα  είναι συνευθειακά,όπως θέλαμε.
είναι συνευθειακά,όπως θέλαμε.