Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
-
Επιτροπή Θεμάτων 2023
- Δημοσιεύσεις: 28
- Εγγραφή: Πέμ Μάιος 12, 2016 9:41 am
Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Αγαπητές/τοί φίλες/οι
Στο θέμα αυτό θα αναρτηθούν (αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου) και, αποκλειστικά, θα λυθούν τα θέματα των Μαθηματικών 2023 (των ημερησίων ΓΕΛ). Επομένως σχολιασμοί-κριτική επί της δυσκολίας κ.λ.π. των θεμάτων θα απομακρύνονται από αυτήν την συζήτηση. Αυτές μπορούν να γίνουν στο Σχόλια στα Μαθηματικά ΓΕΛ 2023
Στο θέμα αυτό θα αναρτηθούν (αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου) και, αποκλειστικά, θα λυθούν τα θέματα των Μαθηματικών 2023 (των ημερησίων ΓΕΛ). Επομένως σχολιασμοί-κριτική επί της δυσκολίας κ.λ.π. των θεμάτων θα απομακρύνονται από αυτήν την συζήτηση. Αυτές μπορούν να γίνουν στο Σχόλια στα Μαθηματικά ΓΕΛ 2023
Λέξεις Κλειδιά:
- Πρωτοπαπάς Λευτέρης
- Συντονιστής
- Δημοσιεύσεις: 2937
- Εγγραφή: Τετ Οκτ 14, 2009 12:20 am
- Τοποθεσία: Πετρούπολη, Αθήνα
- Επικοινωνία:
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Δ1. Έστω η συνάρτηση  με
με 
για την οποία ισχύει
Τότε για έχουμε ότι
έχουμε ότι


και αφού
![\displaystyle{\lim_{x \rightarrow 1} \left[ h(x)(x-1)+2x\right]=\ell \cdot 0 +2 \cdot1=2,} \displaystyle{\lim_{x \rightarrow 1} \left[ h(x)(x-1)+2x\right]=\ell \cdot 0 +2 \cdot1=2,}](/forum/ext/geomar/texintegr/latexrender/pictures/16599bf60de0536dbf77331c6843c93d.png)
έχουμε ότι
![\displaystyle{\lim_{x \rightarrow 1}f(x)=2 \Leftrightarrow \lim_{x \rightarrow 1}\left[ln(2-x)-\frac{1}{x}+\kappa \right]=2 \Leftrightarrow -1+\kappa=2 \Leftrightarrow \kappa =3,} \displaystyle{\lim_{x \rightarrow 1}f(x)=2 \Leftrightarrow \lim_{x \rightarrow 1}\left[ln(2-x)-\frac{1}{x}+\kappa \right]=2 \Leftrightarrow -1+\kappa=2 \Leftrightarrow \kappa =3,}](/forum/ext/geomar/texintegr/latexrender/pictures/4ccc975fe25f5af51161a318b69b75f8.png)
δεδομένου ότι
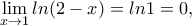

 με
με 
για την οποία ισχύει

Τότε για
 έχουμε ότι
έχουμε ότι

και αφού
![\displaystyle{\lim_{x \rightarrow 1} \left[ h(x)(x-1)+2x\right]=\ell \cdot 0 +2 \cdot1=2,} \displaystyle{\lim_{x \rightarrow 1} \left[ h(x)(x-1)+2x\right]=\ell \cdot 0 +2 \cdot1=2,}](/forum/ext/geomar/texintegr/latexrender/pictures/16599bf60de0536dbf77331c6843c93d.png)
έχουμε ότι
![\displaystyle{\lim_{x \rightarrow 1}f(x)=2 \Leftrightarrow \lim_{x \rightarrow 1}\left[ln(2-x)-\frac{1}{x}+\kappa \right]=2 \Leftrightarrow -1+\kappa=2 \Leftrightarrow \kappa =3,} \displaystyle{\lim_{x \rightarrow 1}f(x)=2 \Leftrightarrow \lim_{x \rightarrow 1}\left[ln(2-x)-\frac{1}{x}+\kappa \right]=2 \Leftrightarrow -1+\kappa=2 \Leftrightarrow \kappa =3,}](/forum/ext/geomar/texintegr/latexrender/pictures/4ccc975fe25f5af51161a318b69b75f8.png)
δεδομένου ότι
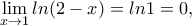

Κάθε πρόβλημα έχει μία τουλάχιστον λύση!!!
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Γιατί πάντα αριθμόν έχοντι. Άνευ τούτου ουδέν νοητόν και γνωστόν.
-
Energy Engineer
- Δημοσιεύσεις: 101
- Εγγραφή: Κυρ Μάιος 02, 2010 9:05 pm
- Τοποθεσία: Γερμανία
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Η γνώμη μου για τα Σωστό -Λάθος μετά από 17 χρόνια μακριά από το αντικείμενο:
α) Σωστό (Τελικά είναι Λάθος, νόμιζα πως ελεγε 0, όχι 1)
β) Λάθος
γ) Σωστό
δ) Λάθος (Σωστό, δεν το πρόσεξα)
ε) Σωστό
α) Σωστό (Τελικά είναι Λάθος, νόμιζα πως ελεγε 0, όχι 1)
β) Λάθος
γ) Σωστό
δ) Λάθος (Σωστό, δεν το πρόσεξα)
ε) Σωστό
τελευταία επεξεργασία από Energy Engineer σε Τρί Ιουν 06, 2023 11:23 am, έχει επεξεργασθεί 2 φορές συνολικά.
- Πρωτοπαπάς Λευτέρης
- Συντονιστής
- Δημοσιεύσεις: 2937
- Εγγραφή: Τετ Οκτ 14, 2009 12:20 am
- Τοποθεσία: Πετρούπολη, Αθήνα
- Επικοινωνία:
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Δ2. Για  έχουμε
έχουμε
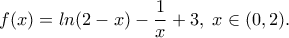
Η συνάρτηση είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 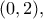 ως άθροισμα των παραγωγίσιμων συναρτήσεων
ως άθροισμα των παραγωγίσιμων συναρτήσεων  [σύνθεση των παραγωγίσιμων
[σύνθεση των παραγωγίσιμων  ] και
] και  [ρητή] και
[ρητή] και  [σταθερή], με
[σταθερή], με
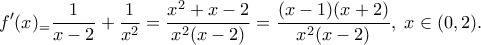
Τότε για έχουμε
έχουμε

αφού
Τότε:
ΣΥΝΗΜΜΕΝΟ ΣΧΗΜΑ
Συνεπώς
* για ισχύει
ισχύει 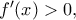 και αφού η f είναι συνεχής στο
και αφού η f είναι συνεχής στο  η
η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![(0,1], (0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/8d0721adae0ada55341b0ddf71336bb7.png)
* για ισχύει
ισχύει  και αφού η f είναι συνεχής στο
και αφού η f είναι συνεχής στο  η
η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
Επίσης
# για η f είναι συνεχής και γνησίως αύξουσα, άρα
η f είναι συνεχής και γνησίως αύξουσα, άρα

#για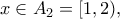 η f είναι συνεχής και γνησίως φθίνουσα, άρα
η f είναι συνεχής και γνησίως φθίνουσα, άρα
![\displaystyle{f(A_2)=\left(\lim_{x \rightarrow 2^-}f(x),f(1)\right)=(-\infty,2].} \displaystyle{f(A_2)=\left(\lim_{x \rightarrow 2^-}f(x),f(1)\right)=(-\infty,2].}](/forum/ext/geomar/texintegr/latexrender/pictures/be6175ff804ab8498e1644adc68d304f.png)
Συνεπώς οπότε η
οπότε η  έχει από μία τουλάχιστον ρίζα στα
έχει από μία τουλάχιστον ρίζα στα  αντίστοιχα και αφού είναι γνησίως μονότονη σε κάθε ένα από αυτά, η εξίσωση
αντίστοιχα και αφού είναι γνησίως μονότονη σε κάθε ένα από αυτά, η εξίσωση  έχει ακριβώς από μία λύση στα
έχει ακριβώς από μία λύση στα 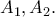
Έστω οι δύο ρίζες με
οι δύο ρίζες με 
 οπότε
οπότε 
Έστω ότι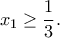
Αφού όπου η
όπου η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  ισχύει
ισχύει
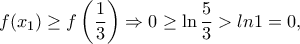
που είναι άτοπο, άρα
και συγκεντρωτικά
Υ.Γ. Μου είχαν ξεφύγει τα βέλη της μονοτονίας. Ευχαριστώ τον Pilgrim για την υπόδειξη
 έχουμε
έχουμε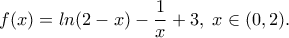
Η συνάρτηση
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 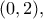 ως άθροισμα των παραγωγίσιμων συναρτήσεων
ως άθροισμα των παραγωγίσιμων συναρτήσεων  [σύνθεση των παραγωγίσιμων
[σύνθεση των παραγωγίσιμων  ] και
] και  [ρητή] και
[ρητή] και  [σταθερή], με
[σταθερή], με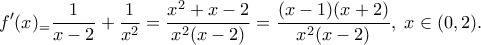
Τότε για
 έχουμε
έχουμε
αφού

Τότε:
ΣΥΝΗΜΜΕΝΟ ΣΧΗΜΑ
Συνεπώς
* για
 ισχύει
ισχύει 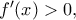 και αφού η f είναι συνεχής στο
και αφού η f είναι συνεχής στο  η
η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![(0,1], (0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/8d0721adae0ada55341b0ddf71336bb7.png)
* για
 ισχύει
ισχύει  και αφού η f είναι συνεχής στο
και αφού η f είναι συνεχής στο  η
η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
Επίσης
# για
 η f είναι συνεχής και γνησίως αύξουσα, άρα
η f είναι συνεχής και γνησίως αύξουσα, άρα
#για
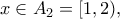 η f είναι συνεχής και γνησίως φθίνουσα, άρα
η f είναι συνεχής και γνησίως φθίνουσα, άρα![\displaystyle{f(A_2)=\left(\lim_{x \rightarrow 2^-}f(x),f(1)\right)=(-\infty,2].} \displaystyle{f(A_2)=\left(\lim_{x \rightarrow 2^-}f(x),f(1)\right)=(-\infty,2].}](/forum/ext/geomar/texintegr/latexrender/pictures/be6175ff804ab8498e1644adc68d304f.png)
Συνεπώς
 οπότε η
οπότε η  έχει από μία τουλάχιστον ρίζα στα
έχει από μία τουλάχιστον ρίζα στα  αντίστοιχα και αφού είναι γνησίως μονότονη σε κάθε ένα από αυτά, η εξίσωση
αντίστοιχα και αφού είναι γνησίως μονότονη σε κάθε ένα από αυτά, η εξίσωση  έχει ακριβώς από μία λύση στα
έχει ακριβώς από μία λύση στα 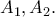
Έστω
 οι δύο ρίζες με
οι δύο ρίζες με 
 οπότε
οπότε 
Έστω ότι
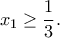
Αφού
 όπου η
όπου η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  ισχύει
ισχύει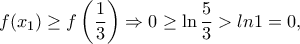
που είναι άτοπο, άρα

και συγκεντρωτικά

Υ.Γ. Μου είχαν ξεφύγει τα βέλη της μονοτονίας. Ευχαριστώ τον Pilgrim για την υπόδειξη
- Συνημμένα
-
- pan_2023_sxhma_d2.png (12.85 KiB) Προβλήθηκε 17043 φορές
τελευταία επεξεργασία από Πρωτοπαπάς Λευτέρης σε Τρί Ιουν 06, 2023 11:41 am, έχει επεξεργασθεί 1 φορά συνολικά.
Κάθε πρόβλημα έχει μία τουλάχιστον λύση!!!
-
Energy Engineer
- Δημοσιεύσεις: 101
- Εγγραφή: Κυρ Μάιος 02, 2010 9:05 pm
- Τοποθεσία: Γερμανία
- Πρωτοπαπάς Λευτέρης
- Συντονιστής
- Δημοσιεύσεις: 2937
- Εγγραφή: Τετ Οκτ 14, 2009 12:20 am
- Τοποθεσία: Πετρούπολη, Αθήνα
- Επικοινωνία:
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
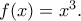
Κάθε πρόβλημα έχει μία τουλάχιστον λύση!!!
- Πρωτοπαπάς Λευτέρης
- Συντονιστής
- Δημοσιεύσεις: 2937
- Εγγραφή: Τετ Οκτ 14, 2009 12:20 am
- Τοποθεσία: Πετρούπολη, Αθήνα
- Επικοινωνία:
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Δ3. Η  ικανοποιεί τις προϋποθέσεις του ΘΜΤ στο
ικανοποιεί τις προϋποθέσεις του ΘΜΤ στο ![\left[x_1,\dfrac{1}{3} \right], \left[x_1,\dfrac{1}{3} \right],](/forum/ext/geomar/texintegr/latexrender/pictures/5b9014e77cd0d191232d1e09125b8849.png) αφού:
αφού:
* η είναι συνεχής στο
είναι συνεχής στο ![\left[x_1,\dfrac{1}{3} \right], \left[x_1,\dfrac{1}{3} \right],](/forum/ext/geomar/texintegr/latexrender/pictures/5b9014e77cd0d191232d1e09125b8849.png)
* η είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 
οπότε υπάρχει ένα τουλάχιστον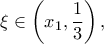 τέτοιο ώστε
τέτοιο ώστε

Τέλος αφού
υπάρχει ένα τουλάχιστον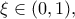 τέτοιο ώστε
τέτοιο ώστε
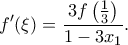
Επίσης η είναι δύο φορές παραγωγίσιμη στο
είναι δύο φορές παραγωγίσιμη στο 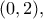
με

οπότε η είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 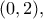
άρα το που βρήκαμε είναι μοναδικό.
που βρήκαμε είναι μοναδικό.
Επομένως, υπάρχει μοναδικό σημείο , με
, με 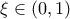 , τέτοιο, ώστε η κλίση
, τέτοιο, ώστε η κλίση  της
της  στο
στο 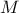 να είναι ίση με
να είναι ίση με 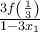 .
.
 ικανοποιεί τις προϋποθέσεις του ΘΜΤ στο
ικανοποιεί τις προϋποθέσεις του ΘΜΤ στο ![\left[x_1,\dfrac{1}{3} \right], \left[x_1,\dfrac{1}{3} \right],](/forum/ext/geomar/texintegr/latexrender/pictures/5b9014e77cd0d191232d1e09125b8849.png) αφού:
αφού:* η
 είναι συνεχής στο
είναι συνεχής στο ![\left[x_1,\dfrac{1}{3} \right], \left[x_1,\dfrac{1}{3} \right],](/forum/ext/geomar/texintegr/latexrender/pictures/5b9014e77cd0d191232d1e09125b8849.png)
* η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 
οπότε υπάρχει ένα τουλάχιστον
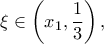 τέτοιο ώστε
τέτοιο ώστε
Τέλος αφού

υπάρχει ένα τουλάχιστον
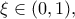 τέτοιο ώστε
τέτοιο ώστε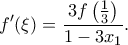
Επίσης η
 είναι δύο φορές παραγωγίσιμη στο
είναι δύο φορές παραγωγίσιμη στο 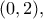
με

οπότε η
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 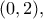
άρα το
 που βρήκαμε είναι μοναδικό.
που βρήκαμε είναι μοναδικό.Επομένως, υπάρχει μοναδικό σημείο
 , με
, με 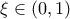 , τέτοιο, ώστε η κλίση
, τέτοιο, ώστε η κλίση  της
της  στο
στο 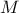 να είναι ίση με
να είναι ίση με 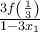 .
.Κάθε πρόβλημα έχει μία τουλάχιστον λύση!!!
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Μια απάντηση για το πολύ καλό Δ4.
i) Είναι
Για έχουμε
έχουμε 
Για έχουμε
έχουμε 
ii) Λόγω της μονοτονίας της συνάρτησης , (γνησίως αύξουσα στο
, (γνησίως αύξουσα στο ![[x_1,1] [x_1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e09814dc5fb6af0dd1dc43891376b386.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![[1,x_2] [1,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/8c32df8202908d997c95c9b4f97ecd45.png) ),
),
θα είναι
Αφού , οι συναρτήσεις
, οι συναρτήσεις  θα είναι γνησίως αύξουσες στο
θα είναι γνησίως αύξουσες στο ![[x_1,x_2] [x_1,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/e2928e128099d8ebc393e5079c62ab4c.png) .
.
Έτσι θα ισχύουν και
και 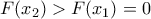 .
.
Έστω η συνάρτηση![\boxed{h(x)=x_1F(x)+x_2G(x)+2x-x_1-x_2}, \ \ x\in [x_1,x_2] \boxed{h(x)=x_1F(x)+x_2G(x)+2x-x_1-x_2}, \ \ x\in [x_1,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/e707c4d77b43f5fa426a67146aa1c572.png) .
.
Είναι και
και 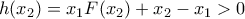 .
.
Από θεώρημα Bolzano η εξίσωση θα έχει ρίζα στο
θα έχει ρίζα στο  , η οποία θα είναι μοναδική, καθώς η
, η οποία θα είναι μοναδική, καθώς η  είναι γνησίως αύξουσα:
είναι γνησίως αύξουσα:
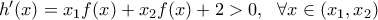 .
.
i) Είναι

Για
 έχουμε
έχουμε 
Για
 έχουμε
έχουμε 
ii) Λόγω της μονοτονίας της συνάρτησης
 , (γνησίως αύξουσα στο
, (γνησίως αύξουσα στο ![[x_1,1] [x_1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e09814dc5fb6af0dd1dc43891376b386.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![[1,x_2] [1,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/8c32df8202908d997c95c9b4f97ecd45.png) ),
), θα είναι

Αφού
 , οι συναρτήσεις
, οι συναρτήσεις  θα είναι γνησίως αύξουσες στο
θα είναι γνησίως αύξουσες στο ![[x_1,x_2] [x_1,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/e2928e128099d8ebc393e5079c62ab4c.png) .
.Έτσι θα ισχύουν
 και
και 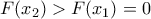 .
.Έστω η συνάρτηση
![\boxed{h(x)=x_1F(x)+x_2G(x)+2x-x_1-x_2}, \ \ x\in [x_1,x_2] \boxed{h(x)=x_1F(x)+x_2G(x)+2x-x_1-x_2}, \ \ x\in [x_1,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/e707c4d77b43f5fa426a67146aa1c572.png) .
.Είναι
 και
και 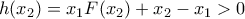 .
.Από θεώρημα Bolzano η εξίσωση
 θα έχει ρίζα στο
θα έχει ρίζα στο  , η οποία θα είναι μοναδική, καθώς η
, η οποία θα είναι μοναδική, καθώς η  είναι γνησίως αύξουσα:
είναι γνησίως αύξουσα: 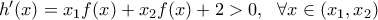 .
.

-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Καλημέρα και από δω !
Πριν ανεβάσει ο Γιώργος το πρώτο Δελτίο, θα έλεγα να μου το στείλει, να κάνω μια ελαφριά γλωσσική επιμέλεια και να δώσω σε όλο το κείμενο την ίδια περίπου ροή.
Δεν θα αλλάξω τίποτα άλλο, παρά μόνο πιθανές εκφραστικές ατέλειες κλπ.
Σε ένα τέταρτο θα το έχω ετοιμάσει.
Ας μου το στείλετε, μια κλήση θα ήταν καλή για το δω αμέσως.
Καλή δύναμη και καλά αποτελέσματα !
Πριν ανεβάσει ο Γιώργος το πρώτο Δελτίο, θα έλεγα να μου το στείλει, να κάνω μια ελαφριά γλωσσική επιμέλεια και να δώσω σε όλο το κείμενο την ίδια περίπου ροή.
Δεν θα αλλάξω τίποτα άλλο, παρά μόνο πιθανές εκφραστικές ατέλειες κλπ.
Σε ένα τέταρτο θα το έχω ετοιμάσει.
Ας μου το στείλετε, μια κλήση θα ήταν καλή για το δω αμέσως.
Καλή δύναμη και καλά αποτελέσματα !
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Μια άλλη ιδέα για το Δ4.
Είναι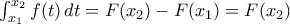 και
και  .
.
Συνεπώς, και άρα
και άρα  ,
,
Επίσης, αφού για κάθε
για κάθε 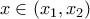 έπεται ότι
έπεται ότι  . Συνεπώς,
. Συνεπώς, 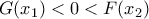 .
.
Τα υπόλοιπα όπως παραπάνω.
Φιλικά,
Αχιλλέας
Είναι
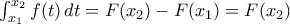 και
και  .
.Συνεπώς,
 και άρα
και άρα  ,
,Επίσης, αφού
 για κάθε
για κάθε 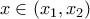 έπεται ότι
έπεται ότι  . Συνεπώς,
. Συνεπώς, 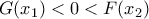 .
.Τα υπόλοιπα όπως παραπάνω.
Φιλικά,
Αχιλλέας
-
DIMITRIS585
- Δημοσιεύσεις: 1
- Εγγραφή: Τρί Νοέμ 02, 2021 9:43 pm
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Μαθητής είμαι. Και εγώ έτσι οπως είπατε τα έλυσα τα 2 ερωτήματα αλλα δεν βρήκα πουθενά τέτοια λύση και αγχώθηκα χωρίς λόγο.Καλο θα είναι όσοι ανεβάζουν λύσεις στα σαιτ να μην γράφουν μόνο μια λύση γιατί τα μαθηματικά είναι φαντασία και δεν πρέπει να περιορίζονται σε μία λύση.Επίσης μπορεί να ξεφεύγω απο το θέμα της συζήτησης αλλά ενώ απο μικρό παιδι συμμετέχω σε μαθηματικούς διαγωνισμούς, δεν μου αρέσουν καθόλου τα μαθηματικά της γ λυκείου. καθε καλοκαιρι ασχολουμαι μονος μου με πραγματα ομορφα για τα μαθηματικα. Εχουν καταντήσει τα μαθηματικά τυποποιημένες λύσεις και θεωρούνται και δύσκολα απο κάποιους!! Σας ευχαριστώ και συγγνώμη αν ξεφυγα απο το θεμα της συζήτησης αλλα ήθελα να πω την άποψη μου!! Καλο υπόλοιπο.
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Το Δ3 χωρίς Θ.Μ.Τ. μπορεί να βγει και με σύνολο τιμών της δεύτερης παραγώγου. Είναι:
 για
για 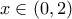
Οπότε η είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  και:
και:
 , αφού είναι:
, αφού είναι:
 ,
,
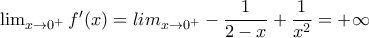
Άρα, και λόγω της μονοτονίας, υπάρχει μοναδικό , τέτοιο ώστε η
, τέτοιο ώστε η  να παίρνει την ζητούμενη τιμή.
να παίρνει την ζητούμενη τιμή.
Θα δείξουμε τώρα ότι θα πρέπει .
.
Είναι:
 , αφού:
, αφού:
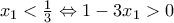 ,
,

Δηλαδή είναι:

 για
για 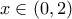
Οπότε η
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  και:
και: , αφού είναι:
, αφού είναι: ,
,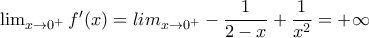
Άρα, και λόγω της μονοτονίας, υπάρχει μοναδικό
 , τέτοιο ώστε η
, τέτοιο ώστε η  να παίρνει την ζητούμενη τιμή.
να παίρνει την ζητούμενη τιμή.Θα δείξουμε τώρα ότι θα πρέπει
 .
.Είναι:
 , αφού:
, αφού: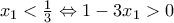 ,
,
Δηλαδή είναι:

τελευταία επεξεργασία από ohgreg σε Τρί Ιουν 06, 2023 4:32 pm, έχει επεξεργασθεί 3 φορές συνολικά.
Ντερέκης Γρηγόρης
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Το έλυσε μαθητής μου με διπλό Θ.Μ.Τ για τις F και G που είναι ουσιαστικά το ίδιο πραγμα
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Αλγεβρική επίλυση στο Β2ii από μαθητή μου


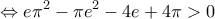
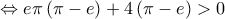



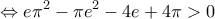
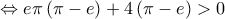

Παντούλας Περικλής
-
Επιτροπή Θεμάτων 2023
- Δημοσιεύσεις: 28
- Εγγραφή: Πέμ Μάιος 12, 2016 9:41 am
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Στην αρχική σελίδα αναρτήθηκε η 1η έκδοση του δελτίου Λύσεων των θεμάτων της σημερινής εξέτασης.
Μπορείτε να τα κατεβάσετε και από εδώ .
Μπορείτε να τα κατεβάσετε και από εδώ .
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Μια προσέγγιση για το δ4 i) (νομίζω αλλάζει λίγο η παρουσίαση , που βασίζεται στις συνέπειες θμτ και αποδεικνύει στην πορεία το πόρισμα, αλλά η ουσία είναι ίδια ..)
Θα χρησιμοποιήσουμε ότι αφού είναι αρχικές της
είναι αρχικές της  στο
στο  τότε:
τότε:
 για κάθε
για κάθε  στο
στο  και επιπλέον
και επιπλέον
 για κάθε
για κάθε  στο
στο 
Αν αφαιρέσουμε κατά μέλη τις παίρνουμε:
παίρνουμε:
 στο
στο  και επομένως
και επομένως
 στο
στο  με
με  στο
στο 
Όμως τότε (από συνέπειες ΘΜΤ)
 για κάθε
για κάθε  στο
στο  και
και  στο
στο 
Θέτω τώρα στην (3) διαδοχικά και
και  και προκύπτει ότι
και προκύπτει ότι  δηλαδη το ζητούμενο λόγο υπόθεσης.
δηλαδη το ζητούμενο λόγο υπόθεσης.
Θα χρησιμοποιήσουμε ότι αφού
 είναι αρχικές της
είναι αρχικές της  στο
στο  τότε:
τότε: για κάθε
για κάθε  στο
στο  και επιπλέον
και επιπλέον  για κάθε
για κάθε  στο
στο 
Αν αφαιρέσουμε κατά μέλη τις
 παίρνουμε:
παίρνουμε: στο
στο  και επομένως
και επομένως  στο
στο  με
με  στο
στο 
Όμως τότε (από συνέπειες ΘΜΤ)
 για κάθε
για κάθε  στο
στο  και
και  στο
στο 
Θέτω τώρα στην (3) διαδοχικά
 και
και  και προκύπτει ότι
και προκύπτει ότι  δηλαδη το ζητούμενο λόγο υπόθεσης.
δηλαδη το ζητούμενο λόγο υπόθεσης.Ο Αρχιμήδης θα μνημονεύεται, όταν ο Αισχύλος θα έχει ξεχαστεί, γιατί, ενώ οι γλώσσες πεθαίνουν, οι μαθηματικές ιδέες είναι διαχρονικές..
Χρήστος Κ.
Χρήστος Κ.
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
Στο Δ2 η ανίσωση για το 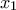 βγαίνει και ως εξής:
βγαίνει και ως εξής:

Όμως είναι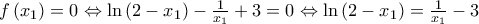
οπότε αντικαθιστώντας στην (1) έχουμε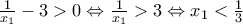
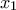 βγαίνει και ως εξής:
βγαίνει και ως εξής: 
Όμως είναι
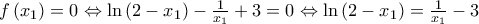
οπότε αντικαθιστώντας στην (1) έχουμε
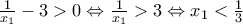
Re: Μαθηματικά ΓΕΛ 2023 (Θέματα & Λύσεις)
ΛΑΘΟΣ ΛΥΣΕΙΣ ΣΤΟ ΘΕΜΑ Γ4 ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΤΩΝ ΠΑΝΕΛΛΗΝΙΩΝ ΤΗΣ 6-6-23
Παίρνω αφορμή από το σημερινό (6-6-23) θέμα Γ4 των Μαθηματικών των Πανελληνίων εξετάσεων για τη λύση του οποίου διαφωνώ με τη συντριπτική πλειονότητα των συναδέλφων που είδα τις λύσεις τους.
Έχω τονίσει σε πολλά από τα 55 βιντεομαθήματά μου με την ύλη της Γ΄ Λυκείου, αλλά και σε διάφορες εισηγήσεις μου έχω αναφέρει ότι, τα όσα ισχυρίζομαι στηρίζονται στα θεωρήματα και τους ορισμούς των σχολικών βιβλίων και φυσικά και σε όλα τα βοηθήματα που ακολουθούν πιστά το σχολικό βιβλίο.
Έχω κάνει ιδιαίτερη αναφορά στη διατύπωση ενός προβλήματος που αφορά τα εμβαδά καμπυλόγραμμων ή μικτόγραμμων χωρίων για τα οποία αναφέρω τα εξής:
ΣΥΜΦΩΝΑ ΜΕ ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΤΗΣ Γ΄ ΛΥΚΕΙΟΥ ως εμβαδόν ενός τέτοιου χωρίου που περικλείεται από 3 ή περισσότερες γραμμές νοείται ΚΑΘΕ εμβαδόν που περικλείεται μεταξύ 2 ή περισσοτέρων από τις δοθείσες γραμμές. Αυτό γίνεται καταφανές από τις σελίδες 227 και 228 του σχολικού βιβλίου, αλλά και από όλα τα βοηθήματα που το ακολουθούν και υπολογίζουν τέτοια εμβαδά.
Για την αποκατάσταση της τάξης, προτείνω να συμπληρώνεται η εκφώνηση ενός τέτοιου προβλήματος με τη φράση: «Βρείτε το εμβαδόν του χωρίου που περικλείεται ΤΑΥΤΟΧΡΟΝΩΣ από τις τάδε γραμμές» ή «Βρείτε το εμβαδόν του χωρίου που περικλείεται από 2 ή περισσότερες από τις τάδε γραμμές». Αν η εκφώνηση ενός τέτοιου προβλήματος δεν συμπληρωθεί με τον παραπάνω τρόπο, το ερώτημα για το ποιο εμβαδόν ζητείται γίνεται ασαφές. Δηλ. ψάχνουμε κάθε εμβαδόν που περικλείεται από τις δοθείσες γραμμές ή ψάχνουμε μόνο εκείνο το εμβαδόν που περικλείεται ταυτόχρονα από όλες τις γραμμές;
Σύμφωνα με το σχολικό βιβλίο, όταν δεν γίνεται αυτή η απαραίτητη διευκρίνιση, βρίσκουμε το άθροισμα όλων των εμβαδών που περικλείονται από τις δοθείσες γραμμές. Στο συγκεκριμένο πρόβλημα του ερωτήματος Γ4 λοιπόν, έπρεπε να βρούμε ΟΛΑ τα εμβαδά που περικλείονται από τη γραφική παράσταση της f, την εφαπτομένη της cf στο σημείο x0=1, τον άξονα των x και την ευθεία x=e και όχι μόνο το εμβαδόν που περικλείεται ταυτόχρονα από τις 4 παραπάνω γραμμές.
Στις λύσεις που είδα, ο υπολογισμός του εμβαδού έγινε μόνο για το χωρίο που περικλείεται ταυτόχρονα και από τις 4 γραμμές, κάτι που δε συμφωνεί με τη λογική του σχολικού βιβλίου. Υπάρχει και εμβαδόν που περικλείεται και από τις εξής γραμμές: Τον άξονα των x, την εφαπτομένη στο σημείο x=1 και την ευθεία x=e.
Έτσι, θεωρώ ότι σωστή είναι η λύση (σύμφωνα με το σχολικό βιβλίο) που υπολογίζει και αυτό το εμβαδόν κάτι που δεν είδα σε καμιά λύση.
Πιο αναλυτικές πληροφορίες σχετικές για το εν λόγω θέμα μπορείτε να δείτε στο βιντεομάθημά μου Νο 54 στη διεύθυνση:
https://www.youtube.com/watch?v=Z2UErF- ... E%AConline
καθώς και στην εισήγησή μου με τίτλο «Ολοκληρώµατα Επισηµάνσεις - ∆ιευκρινίσεις» στις σελίδες 13 και 14 στη διεύθυνση:
http://users.sch.gr/mipapagr/images/ios ... _meros.pdf
Για πολύ περισσότερες παρατηρήσεις και διευκρινίσεις στα ολοκληρώματα, υπάρχουν 5 ακόμη βιντεομαθήματά μου συνολικής διάρκειας σχεδόν 7 ωρών με τίτλους «Ολοκληρώματα: Παρατηρήσεις - Διευκρινίσεις (α), (β), (γ), (δ), (ε)»
(Στα 5 αυτά μαθήματα περιέχονται άλλες παρατηρήσεις και διευκρινίσεις που δεν σχετίζονται με το συγκεκριμένο θέμα).
Παίρνω αφορμή από το σημερινό (6-6-23) θέμα Γ4 των Μαθηματικών των Πανελληνίων εξετάσεων για τη λύση του οποίου διαφωνώ με τη συντριπτική πλειονότητα των συναδέλφων που είδα τις λύσεις τους.
Έχω τονίσει σε πολλά από τα 55 βιντεομαθήματά μου με την ύλη της Γ΄ Λυκείου, αλλά και σε διάφορες εισηγήσεις μου έχω αναφέρει ότι, τα όσα ισχυρίζομαι στηρίζονται στα θεωρήματα και τους ορισμούς των σχολικών βιβλίων και φυσικά και σε όλα τα βοηθήματα που ακολουθούν πιστά το σχολικό βιβλίο.
Έχω κάνει ιδιαίτερη αναφορά στη διατύπωση ενός προβλήματος που αφορά τα εμβαδά καμπυλόγραμμων ή μικτόγραμμων χωρίων για τα οποία αναφέρω τα εξής:
ΣΥΜΦΩΝΑ ΜΕ ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΤΗΣ Γ΄ ΛΥΚΕΙΟΥ ως εμβαδόν ενός τέτοιου χωρίου που περικλείεται από 3 ή περισσότερες γραμμές νοείται ΚΑΘΕ εμβαδόν που περικλείεται μεταξύ 2 ή περισσοτέρων από τις δοθείσες γραμμές. Αυτό γίνεται καταφανές από τις σελίδες 227 και 228 του σχολικού βιβλίου, αλλά και από όλα τα βοηθήματα που το ακολουθούν και υπολογίζουν τέτοια εμβαδά.
Για την αποκατάσταση της τάξης, προτείνω να συμπληρώνεται η εκφώνηση ενός τέτοιου προβλήματος με τη φράση: «Βρείτε το εμβαδόν του χωρίου που περικλείεται ΤΑΥΤΟΧΡΟΝΩΣ από τις τάδε γραμμές» ή «Βρείτε το εμβαδόν του χωρίου που περικλείεται από 2 ή περισσότερες από τις τάδε γραμμές». Αν η εκφώνηση ενός τέτοιου προβλήματος δεν συμπληρωθεί με τον παραπάνω τρόπο, το ερώτημα για το ποιο εμβαδόν ζητείται γίνεται ασαφές. Δηλ. ψάχνουμε κάθε εμβαδόν που περικλείεται από τις δοθείσες γραμμές ή ψάχνουμε μόνο εκείνο το εμβαδόν που περικλείεται ταυτόχρονα από όλες τις γραμμές;
Σύμφωνα με το σχολικό βιβλίο, όταν δεν γίνεται αυτή η απαραίτητη διευκρίνιση, βρίσκουμε το άθροισμα όλων των εμβαδών που περικλείονται από τις δοθείσες γραμμές. Στο συγκεκριμένο πρόβλημα του ερωτήματος Γ4 λοιπόν, έπρεπε να βρούμε ΟΛΑ τα εμβαδά που περικλείονται από τη γραφική παράσταση της f, την εφαπτομένη της cf στο σημείο x0=1, τον άξονα των x και την ευθεία x=e και όχι μόνο το εμβαδόν που περικλείεται ταυτόχρονα από τις 4 παραπάνω γραμμές.
Στις λύσεις που είδα, ο υπολογισμός του εμβαδού έγινε μόνο για το χωρίο που περικλείεται ταυτόχρονα και από τις 4 γραμμές, κάτι που δε συμφωνεί με τη λογική του σχολικού βιβλίου. Υπάρχει και εμβαδόν που περικλείεται και από τις εξής γραμμές: Τον άξονα των x, την εφαπτομένη στο σημείο x=1 και την ευθεία x=e.
Έτσι, θεωρώ ότι σωστή είναι η λύση (σύμφωνα με το σχολικό βιβλίο) που υπολογίζει και αυτό το εμβαδόν κάτι που δεν είδα σε καμιά λύση.
Πιο αναλυτικές πληροφορίες σχετικές για το εν λόγω θέμα μπορείτε να δείτε στο βιντεομάθημά μου Νο 54 στη διεύθυνση:
https://www.youtube.com/watch?v=Z2UErF- ... E%AConline
καθώς και στην εισήγησή μου με τίτλο «Ολοκληρώµατα Επισηµάνσεις - ∆ιευκρινίσεις» στις σελίδες 13 και 14 στη διεύθυνση:
http://users.sch.gr/mipapagr/images/ios ... _meros.pdf
Για πολύ περισσότερες παρατηρήσεις και διευκρινίσεις στα ολοκληρώματα, υπάρχουν 5 ακόμη βιντεομαθήματά μου συνολικής διάρκειας σχεδόν 7 ωρών με τίτλους «Ολοκληρώματα: Παρατηρήσεις - Διευκρινίσεις (α), (β), (γ), (δ), (ε)»
(Στα 5 αυτά μαθήματα περιέχονται άλλες παρατηρήσεις και διευκρινίσεις που δεν σχετίζονται με το συγκεκριμένο θέμα).
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
