paylos έγραψε:Μια άλλη εκδοχή για το Δ1.
Είναι μια λύση, την οποία φαντάζομαι θα επέλεξαν αρκετοί μαθητές με δεδομένο ότι "δουλεύουν" αρκετές ασκήσεις μ' αυτό τον τρόπο.
Mr.Ore έγραψε:Mr.Ore έγραψε:Θα ήθελα να ρωτήσω αν η λύση στο Δ1 με φερμάτ στο 0 είναι λάθος,αφού το πεδίο ορισμού της συνάρτησης που θέτουμε είναι οι πραγματικοί αριθμοί.Στην περίπτωση αυτη πόσα μορια κόβονται;Επίσης στο όριο του Δ2,αν έχω βρει τη σωστή αντικατάσταση,και το όριο της συνάρτησης στο 0,έχοντας όμως αντικαταστήσει μόνο στο ημίτονο ,μπορώ να πάρω 1-2 μόρια;
Oποιος μπορεί ας μου απαντήσει κυρίως για το φερμάτ.
Ευχαριστω!
Θεωρώ ότι η διατύπωση του δεδομένου της ανισότητας, αν και δεν είναι η καλύτερη, αφήνει να καταλάβουμε ότι η ανισότητα ισχύει για τα θετικά

.
Από 'κει και πέρα, η σχέση ισχύει, προφανώς, με το ίσον και στο

και,
για τη συνάρτηση που τελικά προκύπτει,
μπορούμε να δείξουμε ότι ισχύει και για τα αρνητικά

και θα μπορούσε να είναι ένα καλό ζητούμενο του θέματος.
Αυτό όμως, το ότι ισχύει και για τα αρνητικά

δεν μπορούμε να το δείξουμε αν δεν βρούμε την συνάρτηση, ή, τουλάχιστον, την τιμή της στο

και τη μονοτονία της.
Συνεπώς, η εφαρμογή του Fermat στο

είναι λανθασμένη
είτε γιατί το

είναι άκρο του διαστήματος
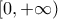
όπου ορίζουμε τη συνάρτηση και για την οποία η ανισότητα ισχύει.
είτε, αν ορίσουμε τη συνάρτηση στο

, δεν γνωρίζουμε ότι στο

έχει ακρότατο, αφού δεν μπορούμε να δείξουμε την ανισότητα για τα αρνητικά

.
Για τη βαθμολόγηση, μια υπόθεση μόνο:
Αν οι βαθμολογητές αποφασίσουν να δώσουν 2 μονάδες για την σωστή εφαρμογή του Fermat, στη θέση

, λογικά θα δώσουν 0 ή 1 μονάδες για την λάθος εφαρμογή στη θέση

.
Για το Δ2 δεν κατάλαβα τι έκανες.

 "
" οπότε αν θέσουμε
οπότε αν θέσουμε  ,
,  έχουμε
έχουμε  x > 0.
x > 0.![\begin{array}{l}
f'\left( x \right) = \frac{{\left( {\ln x - x} \right)^\prime \Phi \left( x \right) - \left( {\ln x - x} \right)\Phi '\left( x \right)}}{{\Phi ^2 \left( x \right)}} = \\
\frac{{\left( {\ln x - x} \right)^\prime \Phi \left( x \right) - \left( {\ln x - x} \right)\frac{{\ln x - x}}{{f\left( x \right)}}}}{{\Phi ^2 \left( x \right)}} = \\
\frac{{\left( {\ln x - x} \right)^\prime }}{{\Phi \left( x \right)}} - \frac{{\left( {\ln x - x} \right)^2 }}{{f\left( x \right)\Phi ^2 \left( x \right)}} = \frac{{\left( {\ln x - x} \right)
^\prime }}{{\Phi \left( x \right)}} - \left[ {\frac{{\left( {\ln x - x} \right)}}{{\Phi \left( x \right)}}} \right]^2 \frac{1}{{f\left( x \right)}} = \\
\frac{{\left( {\ln x - x} \right)^\prime }}{{\Phi \left( x \right)}} - \frac{{f^2 \left( x \right)}}{{f\left( x \right)}} = \frac{{\left( {\ln x - x} \right)^\prime }}{{\Phi \left( x \right)}} -
f\left( x \right) = \frac{{\left( {\ln x - x} \right)^\prime }}{{\frac{{\ln x - x}}{{f\left( x \right)}}}} - f\left( x \right) = \\
f\left( x \right)\frac{{\left( {\ln x - x} \right)^\prime }}{{\ln x - x}} - f\left( x \right) = f\left( x \right)\left[ {\frac{{\left( {\ln x - x} \right)^\prime }}{{\ln x - x}} - 1} \right]. \\
\end{array} \begin{array}{l}
f'\left( x \right) = \frac{{\left( {\ln x - x} \right)^\prime \Phi \left( x \right) - \left( {\ln x - x} \right)\Phi '\left( x \right)}}{{\Phi ^2 \left( x \right)}} = \\
\frac{{\left( {\ln x - x} \right)^\prime \Phi \left( x \right) - \left( {\ln x - x} \right)\frac{{\ln x - x}}{{f\left( x \right)}}}}{{\Phi ^2 \left( x \right)}} = \\
\frac{{\left( {\ln x - x} \right)^\prime }}{{\Phi \left( x \right)}} - \frac{{\left( {\ln x - x} \right)^2 }}{{f\left( x \right)\Phi ^2 \left( x \right)}} = \frac{{\left( {\ln x - x} \right)
^\prime }}{{\Phi \left( x \right)}} - \left[ {\frac{{\left( {\ln x - x} \right)}}{{\Phi \left( x \right)}}} \right]^2 \frac{1}{{f\left( x \right)}} = \\
\frac{{\left( {\ln x - x} \right)^\prime }}{{\Phi \left( x \right)}} - \frac{{f^2 \left( x \right)}}{{f\left( x \right)}} = \frac{{\left( {\ln x - x} \right)^\prime }}{{\Phi \left( x \right)}} -
f\left( x \right) = \frac{{\left( {\ln x - x} \right)^\prime }}{{\frac{{\ln x - x}}{{f\left( x \right)}}}} - f\left( x \right) = \\
f\left( x \right)\frac{{\left( {\ln x - x} \right)^\prime }}{{\ln x - x}} - f\left( x \right) = f\left( x \right)\left[ {\frac{{\left( {\ln x - x} \right)^\prime }}{{\ln x - x}} - 1} \right]. \\
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/85200712ba7c967cf7433a89ee935db6.png)
![\frac{{f'\left( x \right)}}{{f\left( x \right)}} = \left[ {\frac{{\left( {\ln x - x} \right)^\prime }}{{\ln x - x}} - 1} \right] \Leftrightarrow \left( {\ln \left| {f\left( x \right)}
\right|} \right)^\prime = \left( {\ln \left| {\ln x - x} \right| - x} \right)^\prime \frac{{f'\left( x \right)}}{{f\left( x \right)}} = \left[ {\frac{{\left( {\ln x - x} \right)^\prime }}{{\ln x - x}} - 1} \right] \Leftrightarrow \left( {\ln \left| {f\left( x \right)}
\right|} \right)^\prime = \left( {\ln \left| {\ln x - x} \right| - x} \right)^\prime](/forum/ext/geomar/texintegr/latexrender/pictures/a59dc787104bdc35921f6f977c7c94bc.png)



 .
. και,
και, και τη μονοτονία της.
και τη μονοτονία της.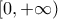 όπου ορίζουμε τη συνάρτηση και για την οποία η ανισότητα ισχύει.
όπου ορίζουμε τη συνάρτηση και για την οποία η ανισότητα ισχύει. , δεν γνωρίζουμε ότι στο
, δεν γνωρίζουμε ότι στο  δεν καταλαβαίνω,γιατί ειναί λάθος το φερμάτ στο 0.Η εκφώνηση δεν ξεκαθάριζε,αν ίσχυε η σχέση για
δεν καταλαβαίνω,γιατί ειναί λάθος το φερμάτ στο 0.Η εκφώνηση δεν ξεκαθάριζε,αν ίσχυε η σχέση για  .
. .
. , όμως το δεδομένο της ανισότητας δεν έχουμε δικαίωμα να το χρησιμοποιήσουμε στο
, όμως το δεδομένο της ανισότητας δεν έχουμε δικαίωμα να το χρησιμοποιήσουμε στο  , η οποία για κάθε
, η οποία για κάθε  ικανοποιεί τη σχέση:
ικανοποιεί τη σχέση:  "
" .
. ⟶
⟶ η οποία για κάθε
η οποία για κάθε 



 τότε πρέπει να πάρει όλες τις μονάδες του ερωτήματος .
τότε πρέπει να πάρει όλες τις μονάδες του ερωτήματος . έχει πεδίο ορισμού το
έχει πεδίο ορισμού το  .
.
 αφού το
αφού το  πράγμα που ισχύει για κάθε
πράγμα που ισχύει για κάθε 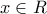
 .Στο
.Στο  .
. .
. για κάθε
για κάθε  , οπότε η
, οπότε η  παρουσιάζει ολικό ελάχιστο για
παρουσιάζει ολικό ελάχιστο για  , οπότε παρουσιάζει και τοπικό ελάχιστο για
, οπότε παρουσιάζει και τοπικό ελάχιστο για  (ως διαφορά συνεχών και πα-ραγωγίσιμων συναρτήσεων), παρουσιάζει και τοπικό ελάχιστο για
(ως διαφορά συνεχών και πα-ραγωγίσιμων συναρτήσεων), παρουσιάζει και τοπικό ελάχιστο για  , οπότε από το θεώρημα του Fermat έχουμε ότι
, οπότε από το θεώρημα του Fermat έχουμε ότι  .
. , οπότε
, οπότε 
 .
. .
.
 είναι η
είναι η  .
. μπροστά από το
μπροστά από το 
 η εξίσωση εφαπτομένης στο
η εξίσωση εφαπτομένης στο  τότε η εξίσωση εφαπτομένης στο
τότε η εξίσωση εφαπτομένης στο  θα είναι
θα είναι  και όχι
και όχι  . Δηλαδή για τον υπολογισμό της κλίσης στο σημείο
. Δηλαδή για τον υπολογισμό της κλίσης στο σημείο ![[f(kx)]' [f(kx)]'](/forum/ext/geomar/texintegr/latexrender/pictures/cabbddade3b2056d039fb230bea2f1dc.png) και στη συνέχεια θέτουμε
και στη συνέχεια θέτουμε  , αλλά απλά θέτουμε στην εξίσωση
, αλλά απλά θέτουμε στην εξίσωση  της εφαπτομένης όπου
της εφαπτομένης όπου ![[f(2x)]' [f(2x)]'](/forum/ext/geomar/texintegr/latexrender/pictures/d1e43431cd4044edb76e61a1032c3349.png) και στη συνέχεια λάβαμε την τιμή στο
και στη συνέχεια λάβαμε την τιμή στο  και όχι η
και όχι η  .
.
