Σελίδα 1 από 1
''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Παρ Δεκ 26, 2008 11:05 pm
από chris_gatos
Ευχαριστώ πολύ για τις λύσεις των συναδέλφων στην προηγούμενη άσκηση...
Συνεχίζω με την εξής άσκηση...
Εστω
![\displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]} \displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e2413e1dbc1b5c2b07ed59d0411c0d3c.png)
συνάρτηση για την οποία ισχύει:

,για κάθε

στο
![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png)
.
Να αποδείξετε οτι

για κάθε

στο
![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png)
.
Υ.Γ: Επεξεργασία σε latex 22/01/2016
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Παρ Δεκ 26, 2008 11:17 pm
από nsmavrogiannis
Χρήστο είναι καλή η εκφώνηση; Φέρνω στο μυαλό μου την

στο
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png)
.
Μαυρογιάννης
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Παρ Δεκ 26, 2008 11:23 pm
από chris_gatos
Κύριε Μαυρογιάννη είναι ακριβώς έτσι η εκφώνηση.Είναι στον πρώτο απο τους 3 τόμους της ''ανάλυσης'' του Τάκη του Βλάμου,σελ 42.
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Παρ Δεκ 26, 2008 11:31 pm
από Mihalis_Lambrou
nsmavrogiannis έγραψε:Χρήστο είναι καλή η εκφώνηση; Φέρνω στο μυαλό μου την

στο
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png)
.
Μαυρογιάννης
Νίκο, η άσκηση ζητά το σύνολο τιμών να είναι στο [α, β], δηλαδή όπως το πεδίο ορισμού.
Οπότε το αντιπαράδειγμά σου δεν κάνει. Και εγώ είχα σκεφτεί ακριβώς το ίδιο
αλλά μετά είδα σωστότερα την εκφώνηση.
Όμως ίσως (λέω, ίσως) η εκφώνηση πρέπει να διορθωθεί σε "f συνεχής".
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Παρ Δεκ 26, 2008 11:34 pm
από nsmavrogiannis
Ωχ! Ούτε που το είδα.
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Παρ Δεκ 26, 2008 11:56 pm
από Mihalis_Lambrou
Με την έξτρα υπόθεση ότι η f είναι συνεχής, να μία απόδειξη:
Η υπόθεση δίνει ότι η f είναι 1-1 (απλό). Άρα, ως συνεχής (!) είναι μονότονη. Χωρίς βλάβη, αύξουσα.
Αν υπάρχουν p, q στο [α, β] με | f(p) – f(q) | > |p – q| τότε, χωρίς βλάβη a < p < q < b.
Έτσι έχουμε (τα απόλυτα φεύγουν διότι f αύξουσα)
f(b) – f(q) > = b – q
f(q) – f(p) > q – p
f(p) – f(a) > = p – a
Προσθέτοντας κατά μέλη f(b) – f(α) > b – α (γνήσια ανίσωση). Άτοπο διότι
f(b) – f(α) < = b – a (αφού το σύνολο τιμών περιέχεται στο [a, b] ).
Για f ασυνεχή, ίδωμεν....
Φιλικά,
Μιχάλης Λάμπρου
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Σάβ Δεκ 27, 2008 12:17 am
από cretanman
Από τα δεδομένα παίρνουμε

Από την άλλη επειδή
![f(x) \in [a,b] f(x) \in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/267575e79c06cd982d90ba43ba4148b5.png)
άρα


και με πρόσθεση των δύο τελευταίων παίρνουμε

έτσι

. Λόγω των

και

παίρνουμε

.
Όμως η τελευταία ισότητα δίνει

και
![f(b)=b] f(b)=b]](/forum/ext/geomar/texintegr/latexrender/pictures/2199dc0725ca3cbc66213eaf971a518d.png)
ειτε

και
![f(b)=a] f(b)=a]](/forum/ext/geomar/texintegr/latexrender/pictures/5b42ef373375ddea58efdee724d1e528.png)
.
Στην πρώτη περίπτωση που

και

: Θέτουμε στην αρχική σχέση
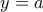
και παίρνουμε

άρα

δηλαδή

, για κάθε
![x\in[a,b] x\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/c7c42309c359c25dfe77f397d5261997.png)
.
Από την άλλη θέτοντας
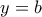
παίρνουμε

δηλαδή

δηλαδή

, για κάθε
![x\in[a,b] x\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/c7c42309c359c25dfe77f397d5261997.png)
.
Συνεπώς
![\boxed{f(x)=x, \ \ \forall x\in[a,b]} \boxed{f(x)=x, \ \ \forall x\in[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/e8015fed3df664a394ea5c88bb66a0b6.png)
Στη δεύτερη περίπτωση που

και

: Θέτουμε
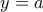
στην αρχική κι έτσι παίρνουμε

δηλαδή

δηλαδή

δηλαδή

για κάθε
![x\in[a,b] x\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/c7c42309c359c25dfe77f397d5261997.png)
.
Από την άλλη, θέτοντας
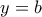
στην αρχική παίρνουμε

δηλαδή

δηλαδή

δηλαδή

, για κάθε
![x\in[a,b] x\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/c7c42309c359c25dfe77f397d5261997.png)
.
Συνεπώς
![\boxed{f(x)=a+b-x, \ \ \forall x\in[a,b]} \boxed{f(x)=a+b-x, \ \ \forall x\in[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/5fe0b77373e17348cae3059cdd5853b4.png)
.
Σε κάθε μία από τις παραπάνω περιπτώσεις ισχύει η ζητούμενη σχέση.
Αλέξανδρος Συγκελάκης
Υ.Γ. Πιστεύω ότι βγαίνει με γρηγορότερο τρόπο καθώς η παραπάνω προσδιορίζει ακριβώς τις συναρτήσεις που επαληθεύουν τη συγκεκριμένη σχέση. Είναι κάτι καλύτερο από αυτό που ζητάει η άσκηση. Φυσικά όλα αυτά, μόνο εάν τα παραπάνω είναι σωστά και δεν έχω χάσει κάπου.
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Σάβ Δεκ 27, 2008 12:42 am
από chris_gatos
Nομίζω Αλέξανδρε πως η λύση σου είναι μαθηματικά άρτια (δεδομένου της περασμένης ώρας).
Καληνύχτα και ευχαριστώ πολύ!
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Σάβ Δεκ 27, 2008 8:59 pm
από k-ser
chris_gatos έγραψε:Εστω f:[α,β]->[α,β] συνάρτηση για την οποία ισχύει:
|f(x)-f(ψ)|>=|χ-ψ|,για κάθε χ,ψ στο [α,β].
Να αποδείξετε οτι |f(x)-f(ψ)|=|χ-ψ| για κάθε χ,ψ στο [α,β]
....................
cretanman έγραψε:
....Συνεπώς
![\boxed{f(x)=x, \ \ \forall x\in[a,b]} \boxed{f(x)=x, \ \ \forall x\in[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/e8015fed3df664a394ea5c88bb66a0b6.png)
![\boxed{f(x)=a+b-x, \ \ \forall x\in[a,b]} \boxed{f(x)=a+b-x, \ \ \forall x\in[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/5fe0b77373e17348cae3059cdd5853b4.png)
....
Βρίσκω καταπληκτικό το αποτέλεσμα που δίνει η απόδειξη του Αλέξανδρου στην πολύ καλή, όπως αποδεικνύεται, έμπνευση της άσκησης.
Μπράβο και στους δύο: Στον Αλέξανδρο και σ΄αυτόν που εμπνεύστηκε την άσκηση για τον οποίο δεν γνωρίζω κατά πόσο είχε υπόψιν του το αποτέλεσμα που δίνει η απόδειξη του Α. ή, αν φτάνει στο ζητούμενο, χωρίς αυτό!
Χρήστο, μήπως γνωρίζεις τη λύση που δίνει ο συγγραφέας;
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Σάβ Δεκ 27, 2008 9:39 pm
από chris_gatos
Την έχει άλυτη κύριε Σερίφη...
Re: ''πονηράδας''....συνέχεια.
Δημοσιεύτηκε: Κυρ Δεκ 28, 2008 1:03 am
από cretanman
k-ser έγραψε:
Μπράβο και στους δύο: Στον Αλέξανδρο και σ΄αυτόν που εμπνεύστηκε την άσκηση για τον οποίο δεν γνωρίζω κατά πόσο είχε υπόψιν του το αποτέλεσμα που δίνει η απόδειξη του Α. ή, αν φτάνει στο ζητούμενο, χωρίς αυτό!
Ευχαριστώ πολύ για τα καλά σας λόγια κύριε Σερίφη!
Αλέξανδρος
![\displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]} \displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e2413e1dbc1b5c2b07ed59d0411c0d3c.png) συνάρτηση για την οποία ισχύει:
συνάρτηση για την οποία ισχύει: ,για κάθε
,για κάθε  στο
στο ![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png) .
. για κάθε
για κάθε  στο
στο ![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png) .
.![\displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]} \displaystyle{f:\left[ {\alpha ,\beta } \right] \to \left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e2413e1dbc1b5c2b07ed59d0411c0d3c.png) συνάρτηση για την οποία ισχύει:
συνάρτηση για την οποία ισχύει: ,για κάθε
,για κάθε  στο
στο ![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png) .
. για κάθε
για κάθε  στο
στο ![\displaystyle{\left[ {\alpha ,\beta } \right]} \displaystyle{\left[ {\alpha ,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/732d2d8cc68c4c7a5e1630eb99f15d40.png) .
. στο
στο ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) .
.
![f(x) \in [a,b] f(x) \in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/267575e79c06cd982d90ba43ba4148b5.png) άρα
άρα
 και με πρόσθεση των δύο τελευταίων παίρνουμε
και με πρόσθεση των δύο τελευταίων παίρνουμε 
 . Λόγω των
. Λόγω των  και
και  παίρνουμε
παίρνουμε  .
. και
και ![f(b)=b] f(b)=b]](/forum/ext/geomar/texintegr/latexrender/pictures/2199dc0725ca3cbc66213eaf971a518d.png) ειτε
ειτε  και
και ![f(b)=a] f(b)=a]](/forum/ext/geomar/texintegr/latexrender/pictures/5b42ef373375ddea58efdee724d1e528.png) .
. και
και  : Θέτουμε στην αρχική σχέση
: Θέτουμε στην αρχική σχέση 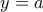 και παίρνουμε
και παίρνουμε  άρα
άρα  δηλαδή
δηλαδή  , για κάθε
, για κάθε ![x\in[a,b] x\in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/c7c42309c359c25dfe77f397d5261997.png) .
.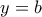 παίρνουμε
παίρνουμε  δηλαδή
δηλαδή  δηλαδή
δηλαδή  , για κάθε
, για κάθε ![\boxed{f(x)=x, \ \ \forall x\in[a,b]} \boxed{f(x)=x, \ \ \forall x\in[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/e8015fed3df664a394ea5c88bb66a0b6.png)
 και
και  : Θέτουμε
: Θέτουμε  δηλαδή
δηλαδή  δηλαδή
δηλαδή  δηλαδή
δηλαδή  για κάθε
για κάθε  δηλαδή
δηλαδή  δηλαδή
δηλαδή  , για κάθε
, για κάθε ![\boxed{f(x)=a+b-x, \ \ \forall x\in[a,b]} \boxed{f(x)=a+b-x, \ \ \forall x\in[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/5fe0b77373e17348cae3059cdd5853b4.png) .
.