Putnam 1988/B4
Δημοσιεύτηκε: Τετ Οκτ 26, 2016 11:15 pm
Να δειχθεί ότι αν η

είναι μια συγκλίνουσα σειρά θετικών αριθμών, τότε η
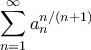
είναι επίσης συγκλίνουσα.

είναι μια συγκλίνουσα σειρά θετικών αριθμών, τότε η
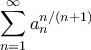
είναι επίσης συγκλίνουσα.
 :
: Αν
Αν  τότε
τότε 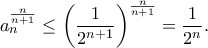
 τότε
τότε 
 ισχύει
ισχύει 
 συγκλίνει, από το Κριτήριο Σύγκρισης έπεται ότι και η σειρά
συγκλίνει, από το Κριτήριο Σύγκρισης έπεται ότι και η σειρά  συγκλίνει.
συγκλίνει.