Σελίδα 1 από 1
Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 2:20 pm
από achilleas
Να υπολογισθεί το όριο

.
Φιλικά,
Αχιλλέας
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 3:18 pm
από Ωmega Man
Αχιλλέα το όριο κάνει 0 μήπως αν όχι στείλε μου πμ να το σβήσω. Αλλιώς θα γράψω μια σκέψη.
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 3:28 pm
από papel
Εαν σπασω το οριο στα δυο μελη η παρανθεση δινει e^n αρα e^(-n)*e^(n)=1.
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 3:29 pm
από silouan
Ελπίζω να μην έχω λάθος. Από το Λήμμα Cesaro έχουμε ότι αρκεί να βρούμε το όριο
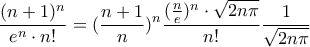
Οι πρώτοι δύο όροι είναι φραγμένοι, αφού ο πρώτος συγκίνει στο

και ο δεύτερος στο 1 (από Stirling), και η τρίτη είναι μηδενική άρα πάει στο 0
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 3:31 pm
από Ωmega Man
Εαν σπασω το οριο στα δυο μελη η παρανθεση δινει e^n αρα e^(-n)*e^(n)=1.
Η σειρά της παρένθεσης είναι η
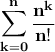
είσαι σίγουρος ότι κάνει
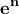
για
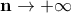
;
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 4:10 pm
από achilleas
Τώρα είδα τις απαντήσεις σας...το όριο δεν είναι ούτε 1 ούτε 0...
Φιλικά,
Αχιλλέας
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 4:14 pm
από Κοτρώνης Αναστάσιος
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 4:15 pm
από papel
Απιστευτο επεσε ακριβως στην μεση των απαντησεων.Τι συμμετρια θεε μου..
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 4:17 pm
από silouan
Tην πάτησα πανυγηρικά !! Αλλά μόλις είδα ότι και ο Αλέξανδρος είχε κανει το ίδιο λάθος.... Εντάξει μπορώ να πω ότι αισθάνομαι τις μισές τύψεις τώρα

Τυχαίο; Δε νομίζω....!"
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 4:29 pm
από p_gianno
Κοτρώνης Αναστάσιος έγραψε:[1 νέος 18 χρονών θα πάρει σύνταξη στα 88! Όλα μαζί 11888. Τυχαίο; Δε νομίζω....!" ]
Αναστάση για μια ακόμη φορά
έγραψες !!
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 4:36 pm
από achilleas
Κοτρώνης Αναστάσιος έγραψε:εδώ
Δε γνώριζα ότι είχε ξαναπροταθεί...ας είναι...νομίζω ότι θα σας αποζημιώσω με την παρακάτω λύση (όχι δική μου)...
Θεωρούμε

ανεξάρτητες τυχαίες μεταβλητές

(
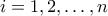
) καθεμια από τις οποίες έχει την κατανομή Poisson με παράμετρο 1.
Τότε η
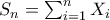
έχει την καταnομή Poisson με παράμετρο

.
Επομένως,
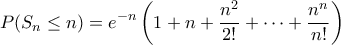
.
Για μεγάλο

, από το central limit theorem, η κατανομή της

προσεγγίζει την κανονική κατανομή με μέση τιμή και διακύμανση

.
Συνεπώς, θα είναι
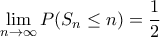
.
Το συμπέρασμα έπεται.
Σχόλια: (1) Το πρόβλημα τέθηκε στο The Mathematical Gazette to 1983. Πολλοί λύτες έστειλαν μια λύση παρόμοια με την παραπάνω! 'Αλλοι προτίμησαν μια πιο αναλυτική προσέγγιση.
(2) Μιά άλλη προσέγγιση συνδυάζει το Θεώρημα προσέγγισης του Taylor, το θεώρημα κυριαρχημένης σύγκλισης και τον τύπο του Stirling.
(3) Ένας τρόπος υπολογισμού του παραπάνω ορίου από τον Ramanujan πάει πίσω ώς το 1911.
Φιλικά,
Αχιλλέας
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 4:44 pm
από Demetres
smar έγραψε:Tην πάτησα πανυγηρικά !! Αλλά μόλις είδα ότι και ο Αλέξανδρος είχε κανει το ίδιο λάθος.... Εντάξει μπορώ να πω ότι αισθάνομαι τις μισές τύψεις τώρα

Σιλουανέ μήπως αντιγράφεις;
 Μάλλον και εγώ αντιγράφω
Μάλλον και εγώ αντιγράφω  Με πρόλαβε ο Αχιλλέας.
Με πρόλαβε ο Αχιλλέας.
Έστω
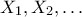
ανεξάρτητες κατανομές Poisson με παράμετρο 1.
Άρα κάθε
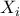
έχει μέση τιμή 1 και τυπική απόκλιση 1. Είναι επίσης γνωστό ότι η
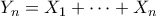
είναι κατανομή Poisson με παράμετρο

.
Από το
κεντρικό οριακό θεώρημα έχουμε
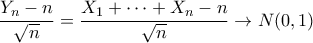
Άρα
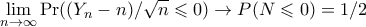
όπου

είναι κανονική κατανομή με μέση τιμή 0 και τυπική απόκλιση 1.
Αλλά
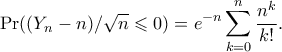
Άρα
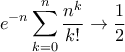
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 4:56 pm
από silouan
Demetres έγραψε:
Σιλουανέ μήπως αντιγράφεις;

Δεν θα το ξανακάνω κύριε...

Μη με μηδενίσετε...
Η λύση με τις πιαθανότητες είναι ΕΠΙΚΗ !!
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 5:05 pm
από Κοτρώνης Αναστάσιος
Ρε παιδιά, το ξεφτυλίσατε το θέμα με τις πιθανότητες! Το πατήσατε καταγής!!! Αχιλλέα οι διαφορετικές λύσεις που λες είχαν σταλεί στο περιοδικό; Πώς μπορεί κανείς να έχει πρόσβαση σε αυτές;
math_finder έγραψε:Κοτρώνης Αναστάσιος έγραψε:[1 νέος 18 χρονών θα πάρει σύνταξη στα 88! Όλα μαζί 11888. Τυχαίο; Δε νομίζω....!" ]
Αναστάση για μια ακόμη φορά
έγραψες !!
Φοβερή ατάκα ε;

Δεν είναι δικής μου έμπνευσης όμως. Κάπου την πέτυχα και έσκασα στα γέλια!!!
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Σάβ Ιουν 05, 2010 5:17 pm
από achilleas
Κοτρώνης Αναστάσιος έγραψε:Ρε παιδιά, το ξεφτυλίσατε το θέμα με τις πιθανότητες! Το πατήσατε καταγής!!! Αχιλλέα οι διαφορετικές λύσεις που λες είχαν σταλεί στο περιοδικό; Πώς μπορεί κανείς να έχει πρόσβαση σε αυτές;
Στο νέο βιβλίο
25 Years of Mathematical Gazette Problem Corner
by The Mathematical Association
που το συνιστώ ανεπιφύλακτα. Έχει όλα τα προβλήματα με τις λύσεις τους στο περιοδικό.
Φιλικά,
Αχιλλέας
Re: Όριο ακολουθίας
Δημοσιεύτηκε: Τετ Μάιος 18, 2011 9:29 pm
από Κοτρώνης Αναστάσιος
Μια ακόμα λύση για την παραπάνω άσκηση, η οποία χρησιμοποιεί την τεχνική που παρουσιάζεται
εδώ.
Ας θέσουμε
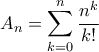
και
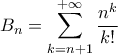
.
Αναζητούμε το
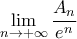
.
Από τον τύπο του Taylor με την ολοκληρωτική μορφή για το υπόλοιπο, έχουμε
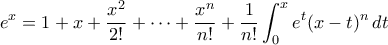
, άρα
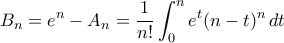
.
Όμως
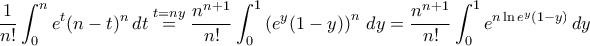
.
Τώρα η
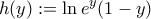
ικανοποιεί τις υποθέσεις της πρότασης 9 σελίδα 45
εδώ, άρα
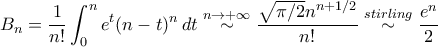
.
Έπεται ότι
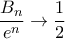
, άρα και
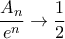
.
 .
. .
. .
.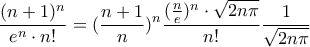
 και ο δεύτερος στο 1 (από Stirling), και η τρίτη είναι μηδενική άρα πάει στο 0
και ο δεύτερος στο 1 (από Stirling), και η τρίτη είναι μηδενική άρα πάει στο 0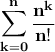 είσαι σίγουρος ότι κάνει
είσαι σίγουρος ότι κάνει 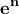 για
για 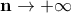 ;
; ανεξάρτητες τυχαίες μεταβλητές
ανεξάρτητες τυχαίες μεταβλητές  (
(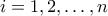 ) καθεμια από τις οποίες έχει την κατανομή Poisson με παράμετρο 1.
) καθεμια από τις οποίες έχει την κατανομή Poisson με παράμετρο 1. 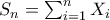 έχει την καταnομή Poisson με παράμετρο
έχει την καταnομή Poisson με παράμετρο  .
.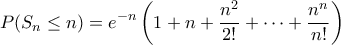 .
. , από το central limit theorem, η κατανομή της
, από το central limit theorem, η κατανομή της  προσεγγίζει την κανονική κατανομή με μέση τιμή και διακύμανση
προσεγγίζει την κανονική κατανομή με μέση τιμή και διακύμανση  .
.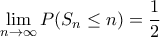 .
.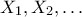 ανεξάρτητες κατανομές Poisson με παράμετρο 1.
ανεξάρτητες κατανομές Poisson με παράμετρο 1. 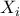 έχει μέση τιμή 1 και τυπική απόκλιση 1. Είναι επίσης γνωστό ότι η
έχει μέση τιμή 1 και τυπική απόκλιση 1. Είναι επίσης γνωστό ότι η 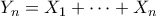 είναι κατανομή Poisson με παράμετρο
είναι κατανομή Poisson με παράμετρο  .
.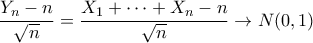
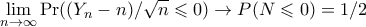
 είναι κανονική κατανομή με μέση τιμή 0 και τυπική απόκλιση 1.
είναι κανονική κατανομή με μέση τιμή 0 και τυπική απόκλιση 1.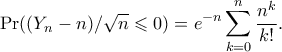
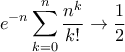

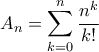 και
και 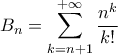 .
.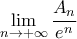 .
.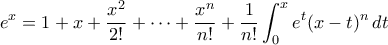 , άρα
, άρα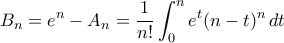 .
.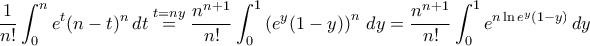 .
.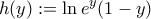 ικανοποιεί τις υποθέσεις της πρότασης 9 σελίδα 45 εδώ, άρα
ικανοποιεί τις υποθέσεις της πρότασης 9 σελίδα 45 εδώ, άρα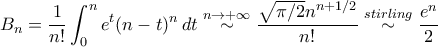 .
.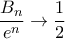 , άρα και
, άρα και 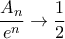 .
.