Δεν πρέπει να συγχέουμε στα Μαθηματικά τις προτάσεις με τους προτασιακούς τύπους.
• Μια πρόταση ή είναι αληθής ή είναι ψευδής .Μια πρόταση δεν είναι άλλοτε αληθής και άλλοτε ψευδής. Η τιμή αληθείας μιας πρότασης δεν μεταβάλλεται. Έτσι για μια πρόταση δεν έχει νόημα να λέμε «είναι αληθής πάντοτε» ή «είναι ψευδής πάντοτε».
• Ένας προτασιακός τύπος μιας μεταβλητής

:
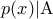
για άλλες τιμές του
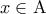
γίνεται μια πρόταση αληθής και για άλλες τιμές του
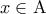
γίνεται μια πρόταση της ψευδής ( όμοια και για έναν προαστιακό τύπο δύο, τριών κλπ μεταβλητών).
• Αν σε ένα προαστιακό τύπο:
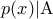
δεσμεύσουμε τη μεταβλητή

με έναν ποσοδείκτη, τότε μετατρέπεται σε πρόταση αληθή ή ψευδή ( όμοια και για έναν προαστιακό τύπο δύο, τριών κλπ μεταβλητών). Για παράδειγμα:
«
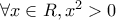
» είναι μια πρόταση ψευδής. «
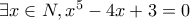
» είναι μια πρόταση αληθής. «
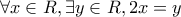
» είναι μια πρόταση αληθείς
Στα θέματα του τύπου «Σωστό –Λάθος» θα πρέπει να δίνουμε μια πρόταση (που έχει μια ορισμένη τιμή αλήθειας) γιατί μόνον τότε θα υπάρχει μονοσήμαντη απάντηση, την οποία και ζητάμε (βλέπε και
εδώ ). Η πρόταση αυτή μπορεί να είναι ποσοδεικτική ή όχι. Αν είναι ποσοδεικτική θα πρέπει φυσικά να αναφέρεται και ο ποσοδείκτης, γιατί διαφορετικά θα πρόκειται για ένα προαστιακό τύπο που δεν έχει μια ορισμένη τιμή αληθείας και επομένως τι θα πρέπει να απαντήσει ο μαθητής; Επειδή όμως τα σύμβολα των ποσοδεικτών δεν είναι γνωστά στους μαθητές,, τους εκφράζουμε με λόγια: « για κάθε», « πάντοτε». « υπάρχει» κτλ. Αν παραλείψουμε την κατάλληλη λέξη , τότε θα δίνουμε έναν προτασιακό τύπο και θα ρωτάμε αν είναι αληθείς ή ψευδής!!!!!!! Για παράδειγμα:
«
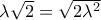
,

». Σωστό- Λάθος.
Τι θα πρέπει να απάντησε ο μαθητής, αφού με

είναι μια πρόταση αληθής, ενώ με
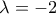
είναι μια πρόταση ψευδής. Το σωστό είναι:
«
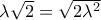
, για κάθε

». Σωστό- Λάθος. Επίσης:
"Υπάρχει

,
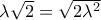
. Σωστό- Λάθος.
• Τα μαθηματικά θεμελιώνονται, κατανοούνται και αναπτύσσονται με τη βοήθεια της μαθηματικής λογικής. Τα μαθηματικά είναι σοβαρή υπόθεση.
 είναι πραγματικός αριθμός)
είναι πραγματικός αριθμός)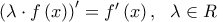
 είναι πραγματικός αριθμός)
είναι πραγματικός αριθμός) :
: 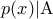 για άλλες τιμές του
για άλλες τιμές του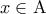 γίνεται μια πρόταση αληθής και για άλλες τιμές του
γίνεται μια πρόταση αληθής και για άλλες τιμές του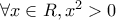 » είναι μια πρόταση ψευδής. «
» είναι μια πρόταση ψευδής. «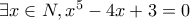 » είναι μια πρόταση αληθής. «
» είναι μια πρόταση αληθής. «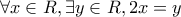 » είναι μια πρόταση αληθείς
» είναι μια πρόταση αληθείς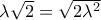 ,
,  ». Σωστό- Λάθος.
». Σωστό- Λάθος. είναι μια πρόταση αληθής, ενώ με
είναι μια πρόταση αληθής, ενώ με 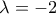 είναι μια πρόταση ψευδής. Το σωστό είναι:
είναι μια πρόταση ψευδής. Το σωστό είναι: