Σελίδα 1 από 1
Ολοκληρώματα
Δημοσιεύτηκε: Δευ Ιουν 30, 2014 3:37 pm
από Tolaso J Kos
Re: Ολοκληρώματα
Δημοσιεύτηκε: Δευ Ιουν 30, 2014 6:08 pm
από BAGGP93
Re: Ολοκληρώματα
Δημοσιεύτηκε: Τρί Ιούλ 01, 2014 12:04 am
από BAGGP93
Re: Ολοκληρώματα
Δημοσιεύτηκε: Τρί Ιούλ 01, 2014 1:37 am
από BAGGP93
Tolaso J Kos έγραψε:
3. 
Έστω
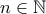
.
Ολοκληρώνουμε είτε στο
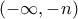
είτε στο
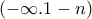
είτε... είτε στο

.
Έστω οι πραγματικές σταθερές
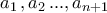
για τις οποίες ισχύει ότι

Τότε,

Για
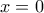
παίρνουμε

Για
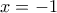
παίρνουμε

Για

παίρνουμε

Συνεχίζουμε μέχρι το
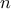
και βλέπουμε ότι

(που εύκολα βλέπουμε ότι επαληθεύουν την

και άρα είναι οι μοναδικοί με αυτήν την ιδιότητα) , οπότε

Ας το επαληθεύσουμε για μικρές τιμές του

.
Αν
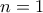
, τότε :

Αν

, τότε :

Re: Ολοκληρώματα
Δημοσιεύτηκε: Τρί Ιούλ 01, 2014 10:39 am
από grigkost
Tolaso J Kos έγραψε:...και ένα πιο δύσκολο το οποίο ξεφεύγει αρκετά από τα παραπάνω:
5. 
Μια λύση:

Χρησιμοποιήθηκαν:
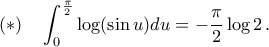
(Εύκολο.)

(Αφήνεται προς το παρόν σαν άσκηση.)
Re: Ολοκληρώματα
Δημοσιεύτηκε: Τρί Ιούλ 01, 2014 12:11 pm
από Tolaso J Kos
grigkost έγραψε:
Χρησιμοποιήθηκαν:
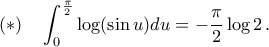
(Εύκολο.)

(Αφήνεται προς το παρόν σαν άσκηση.)
Πάμε κατευθείαν στο δεύτερο ολοκλήρωμα, και λίγο συνοπτικά γιατί πρέπει να φύγω.
Το πρώτο είναι απλό, η αντικατάσταση
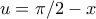
δίνει άμεσα αποτέλεσμα, για όποιον δεν τον έχει ξανά δει.
Για το δεύτερο, ο πιο γρήγορος τρόπος είναι μέσω των συναρτήσεων
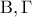
με παράγωγιση δύο φορές. Εδώ θα δώσω έναν άλλο τρόπο που έχω δει για αυτό σε ένα βιβλίο και χρησιμοποιεί σειρές
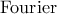
.
Έχουμε ότι:
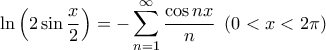
. Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε:

Ολοκληρώνουμε και τα δύο μέλη από

ως
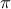
και θα χουμε λοιπόν:
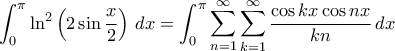
.
Τώρα το δεξί μέλος κάνει:
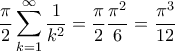
αφού
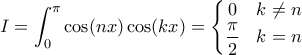
.
To αριστερό μέλος τώρα γίνεται:


Υ.Σ Υπάρχει λύση και με μιγαδική ανάλυση. Δε τη βρίσκω αυτή τη στιγμή να την ανεβάσω. Όποιος θέλει ας το κάνει.
Re: Ολοκληρώματα
Δημοσιεύτηκε: Τρί Ιούλ 01, 2014 3:06 pm
από BAGGP93
Re: Ολοκληρώματα
Δημοσιεύτηκε: Τρί Ιούλ 01, 2014 5:34 pm
από grigkost
Ακόμα μια λύση για το 4ο:
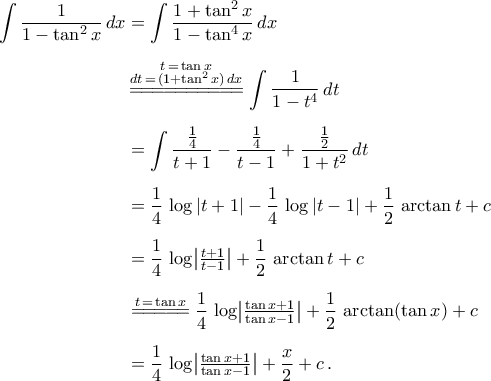
Re: Ολοκληρώματα
Δημοσιεύτηκε: Τρί Ιούλ 01, 2014 6:47 pm
από Σεραφείμ
Re: Ολοκληρώματα
Δημοσιεύτηκε: Τρί Ιούλ 01, 2014 9:14 pm
από Κοτρώνης Αναστάσιος
Tolaso J Kos έγραψε:Έχουμε ότι:
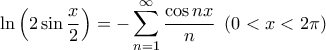
. Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε:

Εδώ χρησιμοποιήθηκε ότι
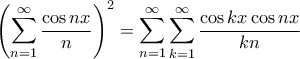
.
Γιατί ισχύει αυτό;
Tolaso J Kos έγραψε:Τώρα το δεξί μέλος κάνει:
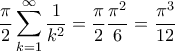
αφού
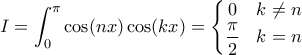
.
Πώς δικαιολογείται παραπάνω η αλλαγή ολοκλήρωσης και αθροίσεων;
Re: Ολοκληρώματα
Δημοσιεύτηκε: Κυρ Αύγ 10, 2014 3:35 pm
από Tolaso J Kos
Κοτρώνης Αναστάσιος έγραψε:Tolaso J Kos έγραψε:Έχουμε ότι:
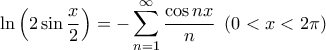
. Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε:

Εδώ χρησιμοποιήθηκε ότι
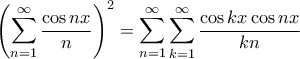
.
Γιατί ισχύει αυτό;
Πρόκειται για γνωστή (?) πρόταση, την οποία όμως δεν την έχω δει σε κανένα βιβλίο γραμμένη. Έχουν χρησιμοποιηθεί και αρκετές φορές στο

, σε υπολογισμούς σειρών (πρόσφατα μάλιστα).
Μία απόδειξη που γνωρίζω είναι η παρακάτω:

Ίδια λογική ισχύει και για τα ολοκληρώματα, δηλ:

όπου
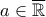
( δε γνωρίζω αν
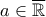
και στις σειρές)
Η τελευταία ιδιότητα (δηλ. των ολοκληρωμάτων) χρησιμοποιείται σε μία από τις πολλές αποδείξεις του
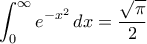
.
Δηλαδή έστω

Και στη συνέχεια προχωράμε με αλλαγή συντεταγμένων σε πολικές, για να πάρουμε τελικά ότι

οπότε και τη ζητούμενη τιμή του

.
Re: Ολοκληρώματα
Δημοσιεύτηκε: Κυρ Αύγ 17, 2014 4:15 pm
από Κοτρώνης Αναστάσιος
Tolaso J Kos έγραψε:Κοτρώνης Αναστάσιος έγραψε:Tolaso J Kos έγραψε:Έχουμε ότι:
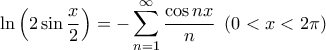
. Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε:

Εδώ χρησιμοποιήθηκε ότι
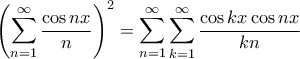
.
Γιατί ισχύει αυτό;
Πρόκειται για γνωστή (?) πρόταση, την οποία όμως δεν την έχω δει σε κανένα βιβλίο γραμμένη. Έχουν χρησιμοποιηθεί και αρκετές φορές στο

, σε υπολογισμούς σειρών (πρόσφατα μάλιστα).
Μία απόδειξη που γνωρίζω είναι η παρακάτω:

Ίδια λογική ισχύει και για τα ολοκληρώματα, δηλ:

όπου
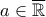
( δε γνωρίζω αν
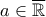
και στις σειρές)
Η τελευταία ιδιότητα (δηλ. των ολοκληρωμάτων) χρησιμοποιείται σε μία από τις πολλές αποδείξεις του
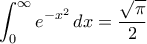
.
Δηλαδή έστω

Και στη συνέχεια προχωράμε με αλλαγή συντεταγμένων σε πολικές, για να πάρουμε τελικά ότι

οπότε και τη ζητούμενη τιμή του

.
Καλησπέρα.
Νομίζω ότι το ερώτημα παραμένει αναπάντητο.










 . Με ολοκλήρωση κατά παράγοντες έχουμε :
. Με ολοκλήρωση κατά παράγοντες έχουμε :




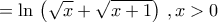 .
. έχουμε :
έχουμε :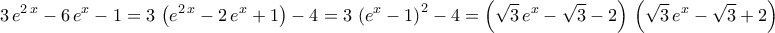 .
.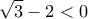 , το διάστημα ολοκλήρωσης είναι το
, το διάστημα ολοκλήρωσης είναι το 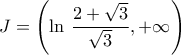 .
.
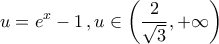 , έχουμε
, έχουμε 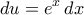 και
και 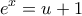 , οπότε :
, οπότε :






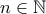 .
.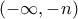 είτε στο
είτε στο 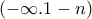 είτε... είτε στο
είτε... είτε στο  .
.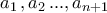 για τις οποίες ισχύει ότι
για τις οποίες ισχύει ότι

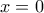 παίρνουμε
παίρνουμε 
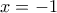 παίρνουμε
παίρνουμε 
 παίρνουμε
παίρνουμε 
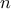 και βλέπουμε ότι
και βλέπουμε ότι 
 και άρα είναι οι μοναδικοί με αυτήν την ιδιότητα) , οπότε
και άρα είναι οι μοναδικοί με αυτήν την ιδιότητα) , οπότε
 .
.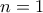 , τότε :
, τότε :
 , τότε :
, τότε :

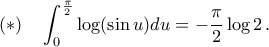 (Εύκολο.)
(Εύκολο.) (Αφήνεται προς το παρόν σαν άσκηση.)
(Αφήνεται προς το παρόν σαν άσκηση.)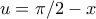 δίνει άμεσα αποτέλεσμα, για όποιον δεν τον έχει ξανά δει.
δίνει άμεσα αποτέλεσμα, για όποιον δεν τον έχει ξανά δει.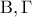 με παράγωγιση δύο φορές. Εδώ θα δώσω έναν άλλο τρόπο που έχω δει για αυτό σε ένα βιβλίο και χρησιμοποιεί σειρές
με παράγωγιση δύο φορές. Εδώ θα δώσω έναν άλλο τρόπο που έχω δει για αυτό σε ένα βιβλίο και χρησιμοποιεί σειρές 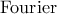 .
.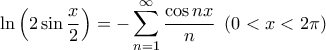 . Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε:
. Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε: 
 ως
ως 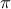 και θα χουμε λοιπόν:
και θα χουμε λοιπόν: 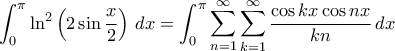 .
.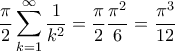 αφού
αφού 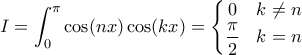 .
.

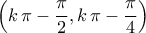 είτε στο
είτε στο 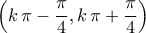 ή στο
ή στο 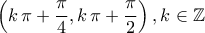 .
.![\displaystyle{\begin{aligned} \int \dfrac{1}{1-\tan^2\,x}\,\rm{dx}&=\int \dfrac{\cos^2\,x}{\cos^2\,x-\sin^2\,x}\,\rm{dx}\\&=\int \dfrac{\cos\,(2\,x)+1}{2\,\cos\,(2\,x)}\,\rm{dx}\\&=\int \left(\dfrac{1}{2\,\cos\,2\,x}+\frac{1}{2}\right)\,\rm{dx}\\&=\int \left(\dfrac{\cos\,2\,x}{2\,\left(1-\sin^2\,2\,x\right)}+\frac{1}{2}\right)\,\rm{dx}\\&=\int \left[\frac{\cos\,2\,x}{4}\,\dfrac{\left(1+\sin\,2\,x\right)+\left(1-\sin\,2\,x\right)}{\left(1-\sin\,2\,x\right)\,\left(1+\sin\,2\,x\right)}+\frac{1}{2}\right]\,\rm{dx}\\&=\int \left[\dfrac{2\,\cos\,2\,x}{8\,\left(1-\sin\,2\,x\right)}+\dfrac{2\,\cos\,2\,x}{8\,\left(1+\sin\,2\,x\right)}+\frac{1}{2}\right]\,\rm{dx}\\&=\frac{1}{8}\,\ln\,\left|1+\sin\,2\,x\right|-\frac{1}{8}\,\ln\,\left|1-\sin\,2\,x\right|+\frac{x}{2}+c\,,c\in\mathbb{R}\end{aligned}} \displaystyle{\begin{aligned} \int \dfrac{1}{1-\tan^2\,x}\,\rm{dx}&=\int \dfrac{\cos^2\,x}{\cos^2\,x-\sin^2\,x}\,\rm{dx}\\&=\int \dfrac{\cos\,(2\,x)+1}{2\,\cos\,(2\,x)}\,\rm{dx}\\&=\int \left(\dfrac{1}{2\,\cos\,2\,x}+\frac{1}{2}\right)\,\rm{dx}\\&=\int \left(\dfrac{\cos\,2\,x}{2\,\left(1-\sin^2\,2\,x\right)}+\frac{1}{2}\right)\,\rm{dx}\\&=\int \left[\frac{\cos\,2\,x}{4}\,\dfrac{\left(1+\sin\,2\,x\right)+\left(1-\sin\,2\,x\right)}{\left(1-\sin\,2\,x\right)\,\left(1+\sin\,2\,x\right)}+\frac{1}{2}\right]\,\rm{dx}\\&=\int \left[\dfrac{2\,\cos\,2\,x}{8\,\left(1-\sin\,2\,x\right)}+\dfrac{2\,\cos\,2\,x}{8\,\left(1+\sin\,2\,x\right)}+\frac{1}{2}\right]\,\rm{dx}\\&=\frac{1}{8}\,\ln\,\left|1+\sin\,2\,x\right|-\frac{1}{8}\,\ln\,\left|1-\sin\,2\,x\right|+\frac{x}{2}+c\,,c\in\mathbb{R}\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/55e3450c89a367054b90b6a9902833f2.png)


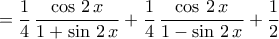





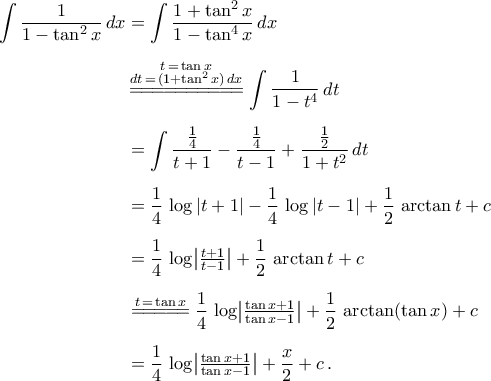
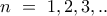 ισχύει
ισχύει 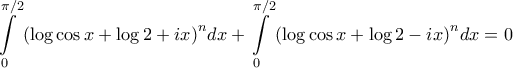 .
. 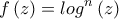 είναι αναλυτική στον ανοιχτό δίσκο
είναι αναλυτική στον ανοιχτό δίσκο 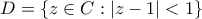 (διότι
(διότι  ), επομένως
), επομένως 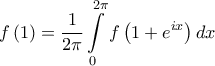 κι επειδή
κι επειδή  , θα ισχύει
, θα ισχύει 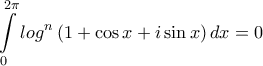 . Άρα ..
. Άρα ..


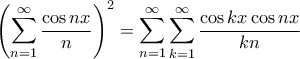 .
.

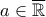 ( δε γνωρίζω αν
( δε γνωρίζω αν 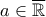 και στις σειρές)
και στις σειρές)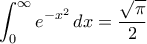 .
.
 οπότε και τη ζητούμενη τιμή του
οπότε και τη ζητούμενη τιμή του  .
.