Σελίδα 1 από 1
Συνάρτηση ολοκλήρωμα
Δημοσιεύτηκε: Τρί Σεπ 22, 2020 3:42 pm
από Tolaso J Kos
Πλέον δεν είναι κατάλληλη για το φάκελο της Γ'.
Δίδεται η συνάρτηση

(α) Να βρεθεί το πεδίο ορισμού της.
(β) Να δειχθεί ότι η

είναι γνησίως φθίνουσα στο

.
(γ) Να δειχθεί ότι για κάθε

είναι

.
(δ) Να δειχθεί ότι για κάθε

είναι

.
Re: Συνάρτηση ολοκλήρωμα
Δημοσιεύτηκε: Τρί Σεπ 22, 2020 6:09 pm
από Mihalis_Lambrou
Tolaso J Kos έγραψε: ↑Τρί Σεπ 22, 2020 3:42 pm
Πλέον δεν είναι κατάλληλη για το φάκελο της Γ'.
Δίδεται η συνάρτηση

(α) Να βρεθεί το πεδίο ορισμού της.
(β) Να δειχθεί ότι η

είναι γνησίως φθίνουσα στο

.
(γ) Να δειχθεί ότι για κάθε

είναι

.
(δ) Να δειχθεί ότι για κάθε

είναι

.
Θα γίνει πολλαπλή χρήση της

από όπου, ειδικά, ο παρονομαστής είναι

.
α) Αφού το πεδίο ορισμού του λογαρίθμου μέσα στο ολοκλήρωμα είναι το
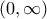
, έπεται ότι πρέπει και

. Από εκεί και πέρα η συνάρτηση δεν έχει άλλο περιορισμό.
β) Παραγωγίζοντας

. O παρονομαστής είναι θετικός
από την

, οπότε η

στο

και άρα η

είναι φθίνουσα εκεί (η εκφώνηση θέλει διόρθωση τυπογραφικού).
γ) Από την
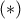
έχουμε

δ) Αφού για

είναι

(ισοδυναμεί με το

) έχουμε


 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  .
. είναι
είναι  .
. είναι
είναι  .
.
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  .
. είναι
είναι  .
. είναι
είναι  .
. από όπου, ειδικά, ο παρονομαστής είναι
από όπου, ειδικά, ο παρονομαστής είναι  .
. 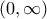 , έπεται ότι πρέπει και
, έπεται ότι πρέπει και  . O παρονομαστής είναι θετικός
. O παρονομαστής είναι θετικός  , οπότε η
, οπότε η  στο
στο  και άρα η
και άρα η 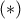 έχουμε
έχουμε 
 είναι
είναι  (ισοδυναμεί με το
(ισοδυναμεί με το  ) έχουμε
) έχουμε 