Έστω ότι το σημείοKARKAR έγραψε:"Χορταστική" , η επίλυση του Κώστα , προσιτή , επίσης , σε όλους τους ενδιαφερόμενους ...
Πάμε για άλλα ( έστω και αν απομακρυνθούμε λίγο , από τον τίτλο του θέματος ) :
Να βρεθεί ( κατασκευασθεί ) σημείοπάνω στον περίκυκλο τριγώνου
, ώστε για κάθε κύκλο
που διέρχεται από τα, και τέμνει τις πλευρές
στα σημεία
αντίστοιχα ,
να προκύπτει :
 κατασκευάστηκε.
κατασκευάστηκε.Παρατηρούμε ότι

οπότε από το θεώρημα Maclaurin (αποδεικνύεται εύκολα) θα υπάρχει σημείο
 της μεγαλύτερης πλευράς
της μεγαλύτερης πλευράς  , ώστε
, ώστε  με το
με το 
να είναι προβολή της τομής του περιγεγραμμένου κύκλου με την εξωτερική διχοτόμο της

Άρα σαν
 μπορεί να θεωρηθεί η τομή του περιγεγραμμένου κύκλου
μπορεί να θεωρηθεί η τομή του περιγεγραμμένου κύκλου  με την εξωτερική διχοτόμο της
με την εξωτερική διχοτόμο της  που κατασκευάζεται εύκολα.
που κατασκευάζεται εύκολα.edit: Απλά μετά την ανάρτηση του Κώστα αφαίρεσα την απόκρυψη.
S.E.Louridas





 γιατί είναι εγγεγραμμένες στο μικρό κύκλο και βλέπουν την ίδια χορδή)
γιατί είναι εγγεγραμμένες στο μικρό κύκλο και βλέπουν την ίδια χορδή)
 και
και  είναι ίσα και συνεπώς
είναι ίσα και συνεπώς  .
.  ισαπέχει από τα σημεία
ισαπέχει από τα σημεία  άρα προκύπτει ("κατασκευάζεται") από την τομή της μεσοκαθέτου της πλευράς
άρα προκύπτει ("κατασκευάζεται") από την τομή της μεσοκαθέτου της πλευράς  και
και  κύκλου.
κύκλου.  τέμνει τον κύκλο σε δύο σημεία:
τέμνει τον κύκλο σε δύο σημεία:  όπως φαίνεται στο δεύτερο σχήμα.
όπως φαίνεται στο δεύτερο σχήμα. , του ορθογωνίου
, του ορθογωνίου  , παίρνω τμήματα
, παίρνω τμήματα  .
. επί των
επί των  αντίστοιχα , έτσι ώστε το
αντίστοιχα , έτσι ώστε το  να είναι
να είναι . Πόσο είναι το εμβαδόν του τετραπλεύρου
. Πόσο είναι το εμβαδόν του τετραπλεύρου  ?
? .
.  του σημείου αυτού
του σημείου αυτού  του ορθογωνίου
του ορθογωνίου της γωνίας
της γωνίας  οι οποίες
οι οποίες 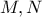 .
.  .
. δίνεται σταθερό σημείο
δίνεται σταθερό σημείο  .
. , με m,n δεδομένα μη μηδενικά ευθύγραμμα τμήματα.
, με m,n δεδομένα μη μηδενικά ευθύγραμμα τμήματα. , με m δεδομένo μη μηδενικό ευθύγραμμο τμήμα.
, με m δεδομένo μη μηδενικό ευθύγραμμο τμήμα. , ως εξής : Φέρω το
, ως εξής : Φέρω το  και το
και το  .
. στο
στο  στο
στο  .
. με ύψος
με ύψος  έχω :
έχω :  .
. , τέμνει την
, τέμνει την  στο
στο  (και στο
(και στο  ).
).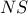 τέμνει την
τέμνει την  στο
στο  . Λόγω της ομοιότητας των ορθογωνίων
. Λόγω της ομοιότητας των ορθογωνίων 

 προϋποθέτει μια μονάδα μέτρησης
προϋποθέτει μια μονάδα μέτρησης  και συμβολίζεται με
και συμβολίζεται με  Άρα από τη στιγμή που μας δίνεται το μήκος, γνωρίζουμε και τη μονάδα μέτρησης.
Άρα από τη στιγμή που μας δίνεται το μήκος, γνωρίζουμε και τη μονάδα μέτρησης.  , τότε θα είναι:
, τότε θα είναι: 
 , τότε θα είναι:
, τότε θα είναι: 
 για το οποίο ισχύει
για το οποίο ισχύει  υψώσαμε κάθετη που έκοψε στον κύκλο
υψώσαμε κάθετη που έκοψε στον κύκλο 

 και χορδή του
και χορδή του  Επί του ενός τόξου, από εκείνα που η χορδή χωρίζει τον κύκλο, δίνονται τα σημεία
Επί του ενός τόξου, από εκείνα που η χορδή χωρίζει τον κύκλο, δίνονται τα σημεία  διάφορα των
διάφορα των  . Κατασκευάστε σημείο
. Κατασκευάστε σημείο  η τομή της χορδής
η τομή της χορδής 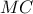 με την
με την 
 η τομή της χορδής
η τομή της χορδής  με την
με την  όπου
όπου  δοθέντα ευθύγραμμα τμήματα.
δοθέντα ευθύγραμμα τμήματα. ενός κύκλου , κατασκευάστε
ενός κύκλου , κατασκευάστε , που να έχουν γινόμενο
, που να έχουν γινόμενο  , όπου
, όπου  "κατάλληλο" , δοθέν τμήμα .
"κατάλληλο" , δοθέν τμήμα . ΄ και κατασκευάζουμε σημείο της
΄ και κατασκευάζουμε σημείο της 
 σύμφωνα με το πνεύμα που είδαμε και από το
σύμφωνα με το πνεύμα που είδαμε και από το  παράλληλη προς την
παράλληλη προς την  (ή κάθετη στην
(ή κάθετη στην  ) που τέμνει τον κύκλο στο σημείο
) που τέμνει τον κύκλο στο σημείο  Από το
Από το  θεωρούμε παράλληλη στην
θεωρούμε παράλληλη στην  που τέμνει την
που τέμνει την 
 τέμνει τον κύκλο στο
τέμνει τον κύκλο στο 
 . Επειδή το τετράπλευρο
. Επειδή το τετράπλευρο  θα έχει τις
θα έχει τις  ,
, η διαγώνιος ) . Αρκεί να κατασκευάσω τη
η διαγώνιος ) . Αρκεί να κατασκευάσω τη  , με κάθετες πλευρές
, με κάθετες πλευρές  . Στη συνέχεια ,
. Στη συνέχεια ,  . Εύκολα διαπιστώνεται ότι πράγματι :
. Εύκολα διαπιστώνεται ότι πράγματι : 
 , δηλαδή πρέπει :
, δηλαδή πρέπει : 
 καθότι έχουμε σαν βάση τα διδόμενα σημεία
καθότι έχουμε σαν βάση τα διδόμενα σημεία  Οπότε από τα ισοσκελή τραπέζια που δημιουργούνται παίρνουμε:
Οπότε από τα ισοσκελή τραπέζια που δημιουργούνται παίρνουμε: 

 να είναι στο ίδιο ημιεπίπεδο με το
να είναι στο ίδιο ημιεπίπεδο με το  Βρείτε επί της (ε) σημείο
Βρείτε επί της (ε) σημείο  ''κατάλληλες'' θετικές σταθερές.
''κατάλληλες'' θετικές σταθερές. όταν δίνονται η πλευρά
όταν δίνονται η πλευρά  , η γωνία
, η γωνία  και το ύψος
και το ύψος  .
. όταν γνωρίζουμε:
όταν γνωρίζουμε: 
 γράφουμε κύκλο. Με διάμετρο το ευθύγραμμο τμήμα
γράφουμε κύκλο. Με διάμετρο το ευθύγραμμο τμήμα  γράφουμε επίσης κύκλο που τέμνει, εν γένει, τον προηγούμενο σε σημείο
γράφουμε επίσης κύκλο που τέμνει, εν γένει, τον προηγούμενο σε σημείο  (είναι δύο τέτοια σημείο, ένα ή κανένα). Αν
(είναι δύο τέτοια σημείο, ένα ή κανένα). Αν  , το
, το  μπορεί να κινηθεί σε κάθε σημείο της ημιευθείας που σχηματίζει με τη
μπορεί να κινηθεί σε κάθε σημείο της ημιευθείας που σχηματίζει με τη  .
.  .
.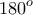 .
.