 , ενός κύκλου
, ενός κύκλου  , διέρχεται από το μέσο
, διέρχεται από το μέσο  της χορδής
της χορδής  . Οι εφαπτόμενες
. Οι εφαπτόμενες στα άκρα της
 τέμνονται στο
τέμνονται στο  , ενώ οι εφαπτόμενες στα άκρα της
, ενώ οι εφαπτόμενες στα άκρα της  τέμνονται στο
τέμνονται στο 
Δείξτε ότι :

Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 , ενός κύκλου
, ενός κύκλου  , διέρχεται από το μέσο
, διέρχεται από το μέσο  της χορδής
της χορδής  . Οι εφαπτόμενες
. Οι εφαπτόμενες  τέμνονται στο
τέμνονται στο  , ενώ οι εφαπτόμενες στα άκρα της
, ενώ οι εφαπτόμενες στα άκρα της  τέμνονται στο
τέμνονται στο 

ΈστωKARKAR έγραψε:Η χορδή, ενός κύκλου
, διέρχεται από το μέσο
της χορδής
. Οι εφαπτόμενες
στα άκρα τηςτέμνονται στο
, ενώ οι εφαπτόμενες στα άκρα της
τέμνονται στο
Δείξτε ότι :
 το κέντρο του «αρχικού κόκκινου κύκλου» τότε
το κέντρο του «αρχικού κόκκινου κύκλου» τότε  εγγράψιμο
εγγράψιμο 
 συνευθειακά και
συνευθειακά και 
 χορδές
χορδές  του περιγεγραμμένου στο
του περιγεγραμμένου στο  κύκλου ισχύει :
κύκλου ισχύει : 
 χορδές
χορδές  του κύκλου
του κύκλου  ισχύει
ισχύει 
 οπότε από το αντίστροφο του θεωρήματος
οπότε από το αντίστροφο του θεωρήματος  είναι εγγράψιμο σε κύκλο
είναι εγγράψιμο σε κύκλο 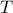 (αφού το
(αφού το  εγγράψιμο
εγγράψιμο 

 τότε
τότε  και η ευθεία
και η ευθεία  με
με  διέρχεται από το
διέρχεται από το 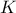
 είναι αντιστοίχως πολικές των σημείων
είναι αντιστοίχως πολικές των σημείων  . Το σημείο
. Το σημείο  ως κοινό σημείο των χορδών
ως κοινό σημείο των χορδών  θα έχει πολική που διέρχεται από τους πόλους των χορδών , δηλαδή την
θα έχει πολική που διέρχεται από τους πόλους των χορδών , δηλαδή την  .
. κάθετη στην
κάθετη στην  .(1)
.(1) ή
ή  κάθετη στην
κάθετη στην  (2)
(2)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης