Πρόκειται για ένα διαισθητικά προφανές θεώρημα που φαίνεται όμως να παρουσιάζει τεχνικές δυσκολίες... Αρχίζω με δύο ανεξαρτήτου ενδιαφέροντος 'βέλτιστες' ανισότητες, κατά τι ισχυρότερες των απαιτουμένων.
Λήμμα 1. Αν

και

τότε

Απόδειξη. Από τις

και

προκύπτει η

και επομένως, ύστερα από λίγες πράξεις, η

.
Λήμμα 2. Αν

και

τότε

.
Απόδειξη.

.
Επιστρέφοντας στο αρχικό πρόβλημα, θεωρούμε μεταβλητό κύκλο

που εφάπτεται των θετικών ημιαξόνων (άρα

) και εφάπτεται επίσης της έλλειψης

σε αναζητούμενο σημείο

(όπου

,

). Προκύπτουν αμέσως οι εξισώσεις

και

. Παρατηρούμε επίσης ότι η εφαπτόμενη κύκλου και έλλειψης είναι κοινή, άρα οι κλίσεις κύκλου και έλλειψης στο

είναι ίσες^ προκύπτει λοιπόν από τις

(κύκλος) και

(έλλειψη) μία τρίτη εξίσωση, η

.
Στόχος μας είναι να δείξουμε ότι το ως προς

,

,

σύστημα τριών εξισώσεων που προέκυψε έχει ακριβώς δύο λύσεις.
Επιλύοντας την πρώτη εξίσωση (δευτεροβάθμια) και την τρίτη εξίσωση (πρωτοβάθμια) ως προς

προκύπτουν οι

και

, άρα και η

. Θέτοντας

(με

) ανάγουμε την τελευταία εξίσωση στην διπλή εξίσωση

.
Είναι φανερό από την

ότι η πρώτη περίπτωση της παραπάνω εξίσωσης,

, δεν έχει λύση για

. Είναι επίσης εύκολο να δούμε ότι έχει μία ακριβώς λύση για

: το δεξιό σκέλος είναι γραμμική αύξουσα συνάρτηση, ενώ το αριστερό σκέλος φθίνει από το

στο

καθώς

(λόγω

).
Προκύπτει από το Λήμμα 1 ότι η δεύτερη περίπτωση της εξίσωσης,

, δεν έχει λύση για

: πράγματι ισχύει, λόγω και της αρνητικότητας του παρονομαστή, η

.
Έχει όμως μία ακριβώς λύση η

για

. Πράγματι, επειδή για

ισχύει η

, ως ισοδύναμη προς την

, είναι φανερό ότι

για

. Είναι επίσης προφανής η

για αρκετά μεγάλο

, άρα υπάρχει σημείο τομής των

και

για κάποιο

. Και δεν μπορεί να υπάρχει δεύτερο σημείο τομής για

καθώς για

η κλίση της

είναι μικρότερη της κλίσης της

λόγω της ανισότητας, για

πάντοτε,

(που είναι ισοδύναμη προς το Λήμμα 2).
Από τα παραπάνω προκύπτει ότι το αρχικό σύστημα έχει όντως δύο ακριβώς λύσεις. Σε συγκεκριμένα παραδείγματα μπορούμε απλώς να υψώσουμε την

στο τετράγωνο για να καταλήξουμε στην τεταρτοβάθμιο

(όπου

), γνωρίζοντας πλέον ότι οφείλει να έχει ακριβώς δύο αποδεκτές θετικές ρίζες. (
Δεν γνωρίζω πως να το αποδείξω αυτό χωρίς την διαδικασία που προηγήθηκε.) Στην περίπτωση της

για παράδειγμα (
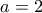
,

) προκύπτουν οι λύσεις

και

, οπότε είναι εύκολος ο προσδιορισμός των

,

από τις

,

και του

από την

: προκύπτουν, για

και

, τα αντίστοιχα σημεία επαφής

και

, και οι αντίστοιχοι κύκλοι

και

. (Τα αποτελέσματα αυτά επαληθεύονται με γράφημα.)
Ανδρέα μας έστειλες ένα υπέροχο πρόβλημα (για το οποίο ξόδεψα τόσο πολύ χαρτί που μου χρωστάς έναν καφέ)! Το πρόβλημα έχει δύο πλευρές: μία θεωρητική για μας (όπου
η προσέγγιση μου δεν είναι υποχρεωτικά η καλύτερη) και μία πρακτική για τους μαθητές (όπως καταδεικνύει η προηγούμενη παράγραφος).
Γιώργος Μπαλόγλου
 με
με  .
.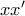 και
και  ,
,  .
.
 και
και  τότε
τότε 
 και επομένως, ύστερα από λίγες πράξεις, η
και επομένως, ύστερα από λίγες πράξεις, η  .
. τότε
τότε  .
. .
. που εφάπτεται των θετικών ημιαξόνων (άρα
που εφάπτεται των θετικών ημιαξόνων (άρα  ) και εφάπτεται επίσης της έλλειψης
) και εφάπτεται επίσης της έλλειψης  (όπου
(όπου  ,
,  ). Προκύπτουν αμέσως οι εξισώσεις
). Προκύπτουν αμέσως οι εξισώσεις  και
και  . Παρατηρούμε επίσης ότι η εφαπτόμενη κύκλου και έλλειψης είναι κοινή, άρα οι κλίσεις κύκλου και έλλειψης στο
. Παρατηρούμε επίσης ότι η εφαπτόμενη κύκλου και έλλειψης είναι κοινή, άρα οι κλίσεις κύκλου και έλλειψης στο  (κύκλος) και
(κύκλος) και  (έλλειψη) μία τρίτη εξίσωση, η
(έλλειψη) μία τρίτη εξίσωση, η  .
.  ,
,  ,
,  σύστημα τριών εξισώσεων που προέκυψε έχει ακριβώς δύο λύσεις.
σύστημα τριών εξισώσεων που προέκυψε έχει ακριβώς δύο λύσεις. και
και  , άρα και η
, άρα και η  . Θέτοντας
. Θέτοντας  (με
(με  ) ανάγουμε την τελευταία εξίσωση στην διπλή εξίσωση
) ανάγουμε την τελευταία εξίσωση στην διπλή εξίσωση  .
. ότι η πρώτη περίπτωση της παραπάνω εξίσωσης,
ότι η πρώτη περίπτωση της παραπάνω εξίσωσης,  , δεν έχει λύση για
, δεν έχει λύση για  . Είναι επίσης εύκολο να δούμε ότι έχει μία ακριβώς λύση για
. Είναι επίσης εύκολο να δούμε ότι έχει μία ακριβώς λύση για  : το δεξιό σκέλος είναι γραμμική αύξουσα συνάρτηση, ενώ το αριστερό σκέλος φθίνει από το
: το δεξιό σκέλος είναι γραμμική αύξουσα συνάρτηση, ενώ το αριστερό σκέλος φθίνει από το  στο
στο  καθώς
καθώς  (λόγω
(λόγω  ).
). , δεν έχει λύση για
, δεν έχει λύση για  .
. ισχύει η
ισχύει η  , ως ισοδύναμη προς την
, ως ισοδύναμη προς την  , είναι φανερό ότι
, είναι φανερό ότι  για
για  για αρκετά μεγάλο
για αρκετά μεγάλο  , άρα υπάρχει σημείο τομής των
, άρα υπάρχει σημείο τομής των  και
και  για κάποιο
για κάποιο  . Και δεν μπορεί να υπάρχει δεύτερο σημείο τομής για
. Και δεν μπορεί να υπάρχει δεύτερο σημείο τομής για  (που είναι ισοδύναμη προς το Λήμμα 2).
(που είναι ισοδύναμη προς το Λήμμα 2). (όπου
(όπου  ), γνωρίζοντας πλέον ότι οφείλει να έχει ακριβώς δύο αποδεκτές θετικές ρίζες. (Δεν γνωρίζω πως να το αποδείξω αυτό χωρίς την διαδικασία που προηγήθηκε.) Στην περίπτωση της
), γνωρίζοντας πλέον ότι οφείλει να έχει ακριβώς δύο αποδεκτές θετικές ρίζες. (Δεν γνωρίζω πως να το αποδείξω αυτό χωρίς την διαδικασία που προηγήθηκε.) Στην περίπτωση της  για παράδειγμα (
για παράδειγμα (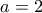 ,
,  ) προκύπτουν οι λύσεις
) προκύπτουν οι λύσεις  και
και  , οπότε είναι εύκολος ο προσδιορισμός των
, οπότε είναι εύκολος ο προσδιορισμός των  ,
,  και
και  , και οι αντίστοιχοι κύκλοι
, και οι αντίστοιχοι κύκλοι  και
και  . (Τα αποτελέσματα αυτά επαληθεύονται με γράφημα.)
. (Τα αποτελέσματα αυτά επαληθεύονται με γράφημα.)