Κατασκευή τριγώνου

dement · #1

Να κατασκευαστεί τρίγωνο με δεδομένη την πλευρά

, το ύψος

και τη διαφορά των πλευρών b-c

.

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

#2

: dement.jpg (21.74 KiB) Προβλήθηκε 1277 φορές

Ανάλυση

γνωστή .. επειδή $\displaystyle{{h_a}}$ γνωστό έχουμε ότι η κορυφή

βρίσκεται επί ευθείας $\displaystyle{\left( \varepsilon \right)}$ παράλληλης της

σε απόσταση $\displaystyle{{h_a}}$ . Επίσης αν φέρουμε τον κύκλο κέντρου

και ακτίνας $\displaystyle{\rho = b - c}$ τότε ο κύκλος κέντρου

και ακτίνας $\displaystyle{R = c}$ , εφάπτεται του $\displaystyle{\left( {C,b - c} \right)}$ και διέρχεται από το

και απ’ το

(συμμετρικό του

ως προς την ευθεία $\displaystyle{\left( \varepsilon \right)}$ ), άρα είναι κατασκευάσιμος (ένα απ’ τα 10 προβλήματα του Απολλώνιου).
Σύνθεση
Κατασκευάζουμε την πλευρά

και ευθεία $\displaystyle{\left( \varepsilon \right)}$ παράλληλη της

σε απόσταση $\displaystyle{{h_a}}$ . Κατασκευάζουμε το σημείο

συμμετρικό του

ως προς $\displaystyle{\left( \varepsilon \right)}$ , καθώς και τον κύκλο $\displaystyle{\left( {C,b - c} \right)}$ . Κατασκευάζουμε τον κύκλο που διέρχεται από τα σημεία

και

και εφάπτεται του $\displaystyle{\left( {C,b - c} \right)}$ . Το κέντρο αυτού του κύκλου είναι το ζητούμενο σημείο

.
Διερεύνηση
Το πρόβλημα δεν έχει λύση αν $\displaystyle{b - c \geqslant a}$ .

H υπόψη κατασκευή του Απολλώνιου (κύκλος διερχόμενος από δυο σημεία και εφαπτόμενος δοθέντος κύκλου) είναι γνωστό πρόβλημα. Θα δοθεί η κατασκευή με την μέθοδο της Αντιστροφής σε κάποια επόμενη ανάρτηση.

dement · #3

Πολύ ωραία Σεραφείμ ! Δίνω και τη δική μου λύση...

Ο παρεγγεγραμμένος κύκλος της

τέμνει την

σε σημείο

με $\displaystyle{AD = \frac{a+c-b}{2}}$ και έχει ακτίνα $\displaystyle{r_C = \frac{a h_a}{a+b-c}}$ . Ομοίως, ο παρεγγεγραμμένος κύκλος της

τέμνει την

σε σημείο

με $\displaystyle{AE = \frac{a+b-c}{2}}$ και έχει ακτίνα $\displaystyle{r_B = \frac{a h_a}{a+c-b}}$ .

Ετσι :

Κατασκευάζουμε κύκλο ακτίνας $\displaystyle{\frac{a h_a}{a+b-c}}$ . Φέρνουμε εφαπτομένη από σημείο

του κύκλου και επιλέγουμε σημείο

επ' αυτής με $\displaystyle{AD = \frac{a+c-b}{2}}$ . Φέρνουμε την άλλη εφαπτομένη στον κύκλο από το

και επιλέγουμε σημείο

επ' αυτής με $\displaystyle{AE = \frac{a+b-c}{2}}$ (το

και το σημείο επαφής με τον κύκλο εκατέρωθεν του

). Κατασκευάζουμε κύκλο ακτίνας $\displaystyle{\frac{a h_a}{a+c-b}}$ με τις AD, AE

κοινές εσωτερικές εφαπτόμενες των κύκλων. Η τομή μιας κοινής εξωτερικής εφαπτομένης των κύκλων και των AE, AD

δίνει τα

.

#4

Σεραφείμ έγραψε: H υπόψη κατασκευή του Απολλώνιου
(κύκλος διερχόμενος από δυο σημεία και εφαπτόμενος δοθέντος κύκλου) είναι γνωστό πρόβλημα.
Θα δοθεί η κατασκευή με την μέθοδο της Αντιστροφής σε κάποια επόμενη ανάρτηση.

Έστω

τα δοθέντα , (X)

αυτός που θέλουμε να κατασκευάσουμε και A,B

σημεία του

αρκεί κατασκευάσουμε τον αντίστροφο του (X)

Αντιστρέφουμε με πόλο το ένα σημείο πχ το

και λόγο τη δύναμη αυτού ως προς τον (C)

o

παραμένει αμετάβλητος

ο (X)

αντιστρέφεται σε ευθεία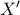

κάθετη στην

,

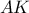το κέντρο του (X)

,

θα είναι εφαπτομένη του (C)

(αφού και τα αρχικά εφάπτονται)

και θα διέρχεται από το

(αντίστροφο του

) - κι αυτό γνωστό

δηλ.το πρόβλημα τώρα μεταφέρεται στην κατασκευή εφαπτομένης από γνωστό σημείο

σε γνωστό κύκλο (C)

... που μπορούμε
-----------------------------------------------
στην περίπτωση που το ένα σημείο πχ το

είναι το σημείο επαφής των δύο κύκλων C(O,R),(X)

τότε

το κέντρο αυτού που θέλουμε να κατασκευάσουμε είναι το σημείο τομής των

και της μεσοκαθέτου του

#5

μία επίσης όμορφη κατασκευή είναι το αδελφάκι αυτής που μας πρότεινε ο Δημήτρης

$\bullet~~:$ Να κατασκευαστεί τρίγωνο με δεδομένη την πλευρά

, το ύψος

και το άθροισμα των πλευρών b+c

.

dement έγραψε:Να κατασκευαστεί τρίγωνο με δεδομένη την πλευρά , το ύψος και τη διαφορά των πλευρών .

dement · #6

Φωτεινή έγραψε:μία επίσης όμορφη κατασκευή είναι το αδελφάκι αυτής που μας πρότεινε ο Δημήτρης

$\bullet~~:$ Να κατασκευαστεί τρίγωνο με δεδομένη την πλευρά , το ύψος και το άθροισμα των πλευρών .

Και το ωραίο είναι ότι αρκεί να αλλάξουμε μερικές λέξεις από την προηγούμενη κατασκευή. Τώρα παίρνουμε τους άλλους δύο από τους τέσσερις τρισεφαπτόμενους κύκλους.

dement έγραψε: Ο εγγεγραμμένος κύκλος τέμνει την σε σημείο με $\displaystyle{AD = \frac{b+c-a}{2}}$ και έχει ακτίνα $\displaystyle{r = \frac{a h_a}{a+b+c}}$ . Ομοίως, ο παρεγγεγραμμένος κύκλος της τέμνει την σε σημείο με $\displaystyle{AE = \frac{a+b+c}{2}}$ και έχει ακτίνα $\displaystyle{r_A = \frac{a h_a}{b+c-a}}$ .

Ετσι :

Κατασκευάζουμε κύκλο ακτίνας $\displaystyle{\frac{a h_a}{a+b+c}}$ . Φέρνουμε εφαπτομένη από σημείο του κύκλου και επιλέγουμε σημείο επ' αυτής με $\displaystyle{AD = \frac{b+c-a}{2}}$ . Φέρνουμε την άλλη εφαπτομένη στον κύκλο από το και επιλέγουμε σημείο επ' αυτής με $\displaystyle{AE = \frac{a+b+c}{2}}$ (το και το σημείο επαφής με τον κύκλο στην ίδια ημιευθεία του ). Κατασκευάζουμε κύκλο ακτίνας $\displaystyle{\frac{a h_a}{b+c-a}}$ με τις κοινές εξωτερικές εφαπτόμενες των κύκλων. Η τομή μιας κοινής εσωτερικής εφαπτομένης των κύκλων και των δίνει τα .

#7

Φωτεινή έγραψε:μία επίσης όμορφη κατασκευή είναι το αδελφάκι αυτής που μας πρότεινε ο Δημήτρης

$\bullet~~:$ Να κατασκευαστεί τρίγωνο με δεδομένη την πλευρά , το ύψος και το άθροισμα των πλευρών .

dement έγραψε:Να κατασκευαστεί τρίγωνο με δεδομένη την πλευρά , το ύψος και τη διαφορά των πλευρών .

Η κατασκευή είναι όμοια με την προηγούμενη με την διαφορά ότι το σημείο

θα είναι το κέντρο κύκλου που θα διέρχεται από τα

και

και θα εφάπτεται κύκλου με κέντρο το

και ακτίνα $\displaystyle{\rho = b + c}$ .[attachment=0]27-02-2012-3.jpg[/attachment]

#8

Με την άδεια του Δημήτρη

ας το επεκτείνουμε λιγάκι .. Να κατασκευαστεί τρίγωνο, στο οποίο δίδεται η πλευρά

κατά θέση και μέγεθος, η διαφορά b-c

καθώς και ότι η κορυφή

βρίσκεται σε σταθερή ευθεία $\displaystyle{\left( \varepsilon \right)}$ .[attachment=0]27-02-2912-4.jpg[/attachment]

Κατασκευή τριγώνου

Κατασκευή τριγώνου

Re: Κατασκευή τριγώνου

Re: Κατασκευή τριγώνου

Re: Κατασκευή τριγώνου

Re: Κατασκευή τριγώνου

Re: Κατασκευή τριγώνου

Re: Κατασκευή τριγώνου

Re: Κατασκευή τριγώνου

Μέλη σε σύνδεση