
Τα σημεία

είναι συνευθειακά γιατί οι ακτίνες

των κύκλων

αντιστοίχως, είναι κάθετες στην κοινή εφαπτομένη τους.
Η δια του

κάθετη ευθεία επί την χορδή

του

είναι μεσοκάθετη σ' αυτήν και τέμνει τον

στο σημείο έστω

προς το μέρος της

που δεν είναι ο κύκλος

Από

και

σύμφωνα με το
Θεώρημα Θαλή, έχουμε ότι τα σημεία
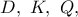
είναι συνευθειακά.
Ομοίως, αποδεικνύεται ότι τα σημεία

είναι συνευθειακά καθώς επίσης και τα σημεία

Είναι εύκολο τώρα να δούμε, ότι η κοινή εφαπτομένη των κύκλων

περνάει από το σημείο

ως το ριζικό κέντρο των κύκλων

και το
(3) ζητούμενο έχει αποδειχθεί.

Τα τρίγωνα

είναι όμοια,
γιατί έχουν

και άρα έχουμε,

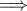


Από

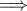

και έτσι συμπεραίνουμε, ότι ο γεωμετρικός τόπος του σημείου επαφής

των κύκλων

είναι το τόξο

του κύκλου

με κέντρο το

και ακτίνα

και το
(2) ζητούμενο έχει αποδειχθεί.
Σημειώνεται ως γνωστό, ότι το σημείο

είναι το έγκεντρο του τριγώνου

όπου


Όπως αποδείχτηκε ότι η ευθεία

περνάει από το μέσον του τόξου

του κύκλου

που δεν εφάπτεται στον κύκλο

ομοίως αποδεικνύεται ότι η ευθεία

περνάει από το μέσον

του τόξου

του

που δεν εφάπτεται στον

Ομοίως η ευθεία

περνάει από το μέσον

του τόξου
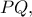
που δεν εφάπτεται στον κύκλο

Άρα, συμπεραίνουμε ότι τα σημεία

είναι συνευθειακά και ότι

και το
(4) ζητούμενο έχει αποδειχθεί.
Κώστας Βήττας.
ΥΓ. Για το
(1) ζητούμενο θα επανέλθω, αφού ψάξω να βρώ την απόδειξη του Κώστα στην οποία αναφέρθηκα πιο πάνω.
 βρίσκονται σε σταθερή παραβολή, της οποίας να βρεθεί η εστία και η διευθετούσα.
βρίσκονται σε σταθερή παραβολή, της οποίας να βρεθεί η εστία και η διευθετούσα. βρίσκεται σε σταθερό κύκλο, του οποίου να βρεθεί το κέντρο και η ακτίνα.
βρίσκεται σε σταθερό κύκλο, του οποίου να βρεθεί το κέντρο και η ακτίνα. των κύκλων
των κύκλων  και οι ευθείες
και οι ευθείες  , συντρέχουν σε σταθερό σημείο.
, συντρέχουν σε σταθερό σημείο. , βρίσκονται επί ευθείας παράλληλης της
, βρίσκονται επί ευθείας παράλληλης της  .
.

 του δοσμένου κύκλου
του δοσμένου κύκλου  και όχι απαραίτητα για διάμετρό του και θα βάλω αργότερα τις αποδείξεις που έχω υπόψη μου.
και όχι απαραίτητα για διάμετρό του και θα βάλω αργότερα τις αποδείξεις που έχω υπόψη μου. δεν έχω κάποια λύση υπόψη μου.
δεν έχω κάποια λύση υπόψη μου.  Τα σημεία
Τα σημεία  είναι συνευθειακά γιατί οι ακτίνες
είναι συνευθειακά γιατί οι ακτίνες  των κύκλων
των κύκλων  αντιστοίχως, είναι κάθετες στην κοινή εφαπτομένη τους.
αντιστοίχως, είναι κάθετες στην κοινή εφαπτομένη τους. κάθετη ευθεία επί την χορδή
κάθετη ευθεία επί την χορδή  είναι μεσοκάθετη σ' αυτήν και τέμνει τον
είναι μεσοκάθετη σ' αυτήν και τέμνει τον  προς το μέρος της
προς το μέρος της 
 και
και  σύμφωνα με το Θεώρημα Θαλή, έχουμε ότι τα σημεία
σύμφωνα με το Θεώρημα Θαλή, έχουμε ότι τα σημεία 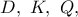 είναι συνευθειακά.
είναι συνευθειακά. είναι συνευθειακά καθώς επίσης και τα σημεία
είναι συνευθειακά καθώς επίσης και τα σημεία 
 περνάει από το σημείο
περνάει από το σημείο  ως το ριζικό κέντρο των κύκλων
ως το ριζικό κέντρο των κύκλων  και το (3) ζητούμενο έχει αποδειχθεί.
και το (3) ζητούμενο έχει αποδειχθεί. είναι όμοια,
είναι όμοια,

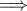



 και έτσι συμπεραίνουμε, ότι ο γεωμετρικός τόπος του σημείου επαφής
και έτσι συμπεραίνουμε, ότι ο γεωμετρικός τόπος του σημείου επαφής  του κύκλου
του κύκλου  με κέντρο το
με κέντρο το  και ακτίνα
και ακτίνα  και το (2) ζητούμενο έχει αποδειχθεί.
και το (2) ζητούμενο έχει αποδειχθεί. όπου
όπου 
 περνάει από το μέσον του τόξου
περνάει από το μέσον του τόξου  ομοίως αποδεικνύεται ότι η ευθεία
ομοίως αποδεικνύεται ότι η ευθεία  περνάει από το μέσον
περνάει από το μέσον  του τόξου
του τόξου  του
του  περνάει από το μέσον
περνάει από το μέσον  του τόξου
του τόξου 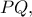 που δεν εφάπτεται στον κύκλο
που δεν εφάπτεται στον κύκλο 
 είναι συνευθειακά και ότι
είναι συνευθειακά και ότι  και το (4) ζητούμενο έχει αποδειχθεί.
και το (4) ζητούμενο έχει αποδειχθεί.
 όταν η
όταν η  , είναι το τμήμα παραβολής με χορδή
, είναι το τμήμα παραβολής με χορδή 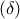 σε παράλληλη απόσταση
σε παράλληλη απόσταση  από την
από την  όπου
όπου 
 . Η απόδειξη του Κώστα είναι πλήρης. Μια αντίστοιχη απόδειξη είχε δοθεί και εδώ ..
. Η απόδειξη του Κώστα είναι πλήρης. Μια αντίστοιχη απόδειξη είχε δοθεί και εδώ ..  (σχήμα 1). Τότε ο κύκλος
(σχήμα 1). Τότε ο κύκλος  αντιστρέφεται στην ευθεία
αντιστρέφεται στην ευθεία  ως εφαπτόμενοι των παραπάνω γραμμών, αλλά και μεταξύ τους, παραμένουν αμετάβλητοι, επομένως η κοινή τους εφαπτομένη διέρχεται από το σταθερό σημείο
ως εφαπτόμενοι των παραπάνω γραμμών, αλλά και μεταξύ τους, παραμένουν αμετάβλητοι, επομένως η κοινή τους εφαπτομένη διέρχεται από το σταθερό σημείο  , δηλαδή βρίσκεται σε σταθερό κύκλο κέντρου
, δηλαδή βρίσκεται σε σταθερό κύκλο κέντρου  .
.  , τα σημεία
, τα σημεία 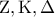 είναι συνευθειακά, ομοίως και
είναι συνευθειακά, ομοίως και  .
. στο σχήμα 2. Επομένως τα σημεία
στο σχήμα 2. Επομένως τα σημεία  είναι συνευθειακά.
είναι συνευθειακά. . Λόγω παραβολής
. Λόγω παραβολής  . Όμοια
. Όμοια  .
.  , καθώς και
, καθώς και  .
. , δηλαδή
, δηλαδή  και τελικά
και τελικά  .
.
 τέμνονται τέμνονται στο ίδιο σημείο έστω
τέμνονται τέμνονται στο ίδιο σημείο έστω  το οποίο ανήκει στην ευθεία
το οποίο ανήκει στην ευθεία 
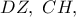 ανήκει στην ευθεία
ανήκει στην ευθεία  ανήκει στην ευθεία
ανήκει στην ευθεία 