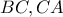 και
και  τριγώνου
τριγώνου  θεωρούμε τα σημεία
θεωρούμε τα σημεία  και
και  αντίστοιχα. Συμβολίζουμε με
αντίστοιχα. Συμβολίζουμε με  και
και  τα εμβαδά των τριγώνων
τα εμβαδά των τριγώνων  και
και  αντίστοιχα.
αντίστοιχα.(i) Να αποδείξετε ότι
 .
.(ii) Πότε ισχύει το ίσον στην παραπάνω ανισότητα;
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
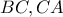 και
και  τριγώνου
τριγώνου  θεωρούμε τα σημεία
θεωρούμε τα σημεία  και
και  αντίστοιχα. Συμβολίζουμε με
αντίστοιχα. Συμβολίζουμε με  και
και  τα εμβαδά των τριγώνων
τα εμβαδά των τριγώνων  και
και  αντίστοιχα.
αντίστοιχα. .
.



 και
και  έχουν κοινή γωνία την
έχουν κοινή γωνία την  άρα
άρα
 και
και 


 που ισχύει.
που ισχύει. , δηλαδή όταν
, δηλαδή όταν 
 διέρχονται από το ίδιο σημείο.
διέρχονται από το ίδιο σημείο. οπότε προφανώς ισχύει
οπότε προφανώς ισχύει  . (1)
. (1)

 .
.

 . (2)
. (2) από τις σχέσεις (1) (και μετά τις πράξεις)
από τις σχέσεις (1) (και μετά τις πράξεις) , η οποία προφανώς ισχύει.
, η οποία προφανώς ισχύει. , οπότε, λόγω του αντίστροφου του θεωρήματος του Ceva αν-ν οι σεβιανές
, οπότε, λόγω του αντίστροφου του θεωρήματος του Ceva αν-ν οι σεβιανές  συντρέχουν.
συντρέχουν. , τότε:
, τότε: .
. (I.M.O. 1966, Θέμα 6).
(I.M.O. 1966, Θέμα 6).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης