Ετοιμαζόμαστε για τις εξετάσεις

#1

ΑΣΚΗΣΗ 1. Δίνεται κύκλος με διάμετρο ΑΒ και πάνω σε αυτόν παίρνουμε το σημείο Γ έτσι, ώστε το τόξο ΑΓ να είναι 60 μοιρών. Αν η χορδή ΒΓ είναι $6\sqrt{3}cm$
(α) Να υπολογήσετε το μήκος της χορδής ΑΓ

(β) Ένα κύλινδρικό κουτάκι έχει βάση τον πιο πάνω κυκλικό δίσκο και το ύψος του είναι 30 cm.
(1) Ποιο είναι το εμβαδόν της κυρτής (παράπλευρης) επιφάνειας;

(2) Πόσα λίτρα (με προσέγγιση εκατοστού) νερό χωρούν στο κουτάκι;

#2

ΑΣΚΗΣΗ 2. Το ύψος ενός (ορθού) πρίσματος είναι (σε cm) ακέραιος αριθμός και ικανοποιεί τις ανισώσεις: $u+1<\frac{17+u}{3},\frac{2u-5}{2}>5-\frac{u}{2}$

Η βάση του πρίσματος είναι ορθογώνιο τρίγωνο με υποτείνουσα 10 cm και μια κάθετη πλευρά 6 cm. Να βρείτε το εμβαδόν της ολικής επιφάνειας και τον όγκο του πρίσματος.

ΑΡΣΕΝΟΗ · #3

ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 2. Το ύψος ενός (ορθού) πρίσματος είναι (σε cm) ακέραιος αριθμός και ικανοποιεί τις ανισώσεις: $u+1<\frac{17+u}{3},\frac{2u-5}{2}>5-\frac{u}{2}$

Η βάση του πρίσματος είναι ορθογώνιο τρίγωνο με υποτείνουσα 10 cm και μια κάθετη πλευρά 6 cm. Να βρείτε το εμβαδόν της ολικής επιφάνειας και τον όγκο του πρίσματος.

Χαιρετώ το

...
Έχουμε απο τη πρώτη ανίσωση:
$\upsilon +1<\frac{17+\upsilon }{3}\Rightarrow 3\upsilon +3<17+\upsilon \Rightarrow 2\upsilon <14\Rightarrow \upsilon <7$
και απο τη δεύτερη:
$\frac{2\upsilon -5}{2}>5-\frac{\upsilon }{2}\Rightarrow 2\upsilon -5>10-\upsilon \Rightarrow 3\upsilon >15\Rightarrow \upsilon >5$
Αφού μας λέει οτι το ύψος είναι ακέραιος αριθμός που ικανοποιεί αυτές τις δύο ανισώσεις, ο μοναδικός αριθμός που είναι ακέραιος είναι ο υ=6.
Αφού η βάση του πρίσματος είναι ορθογώνιο τρίγωνο, εύκολα βρίσκουμε και την δευτερη κάθετη πλευρά απο πυθαγόρειο.Έχουμε:
$10^{2}=x^{2}+6^{2}$
Άρα x=8

Τώρα για το εμβαδόν της ολικής επιφάνειας:
Εολ=Επ+2Εβ=24.6+2.24=144+48=192 $cm^{2}$
Και για τον όγκο:
$V=E\beta {\cdot}\upsilon =24{\cdot}6=144cm^{3}$

Γιώτα · #4

α)
Η γωνία C είναι ορθή καθώς βαίνει στη διάμετρο του κύκλου.
Η γωνία Β είναι ίση με 30 μοίρες καθως βαίνει στο τόξο των 60 μοιρών.
Αρα η πλευρά ΑC του ορθογωνίου τριγώνου ΑΒC είναι ίση με το μίσο της πλευράς ΒΑ.
Επομένως 2ΑC=ΑΒ.
Αρα $AC^{2}+CB^{2}=(2AC)^{2}\Rightarrow AC^{2}+(6\sqrt{3})^{2} =4AC^{2}\Rightarrow AC^{2}+108=4AC^{2}\Rightarrow 108=3AC^{2}\Rightarrow 36=AC^{2}\Rightarrow AC=6$

β1)
Το Ε της κυρτής επιφάνειας είναι ίσο με την περίμετρο του κύκλου επί το ύψος που είναι 30cm.
$2\pi\varrho =2\times 3,14\times6 =37,68$ cm
$E=30\times 37,68=1130,4 cm^{2}$

β2)
Θα πρέπει να βρώ τον όγκο από το κουτάκι που είναι ίσος με:
Ε(κύκλου) επί το ύψος 30cm
Ε(κύκλου)= $\pi\times \rho ^{2}=3,14\times 6^{2}=113,04cm^{2}$
V(κύκλου)= $113,04\times 30=3391,20\simeq 3391cm^{3}$
Αρα είναι 3,39 λίτρα.

Υ.Γ Ελπιζω να μην εχω κάνει λάθος γιατι είναι αργά και πρέπει να παω για ύπνο!

pana1333 · #5

Άσκηση 3

: κύκλοι_.PNG (15.12 KiB) Προβλήθηκε 5318 φορές

Δίνονται τρεις κύκλοι με κέντρα Κ,Μ,Λ και αντίστοιχες διάμετρους $\delta _{1}=\frac{3x}{5}$ , $\delta _{2}=\frac{6x}{15}$ και ΒΓ. Δίνεται επίσης ΑΒ=8cm, ΑΓ=6cm.

α)Να βρεθεί ο αριθμός x και οι ακτίνες $\rho _{1},\rho _{2},\rho _{3}$ των κύκλων με κέντρα Κ,Μ και Λ αντίστοιχα.
β) Να υπολογίσετε τις περίμετρους των τριών κύκλων.
γ) Να υπολογιστει το εμβαδόν του τριγώνου ΑΒΓ.
δ) Να υπολογιστεί το εμβαδόν της γραμμοσκιασμένης (κίτρινης) επιφάνειας
ε) Αν η γωνία B είναι 36 μοίρες, να υπολογιστεί το εμβαδόν του κυκλικού τομέα (ΔΚΕ) και του κυκλικού τομέα (ΜΖΕ).

ΑΡΣΕΝΟΗ · #6

Καλησπέρα...
για την άσκηση 3.
α)Η γωνία Α είναι ορθή καθώς βαίνει στη διάμετρο του κύκλου ρ3.Έτσι απο Π.Θ βρίσκουμε την υποτείνουσα του τριγώνου ΑΒΓ,που είναι και η διάμετρος του κύκλου ρ3.Έχουμε:
$B\Gamma ^{2}=A\Gamma ^{2}+AB^{2}$
$B\Gamma ^{2}=36+64$
$B\Gamma =10$
Αφού η διάμετρος είναι 10cm η ακτίνα θα είναι 5cm.
Τώρα για τις ακτίνες των ρ1 και ρ2:
Αφού τα κέντρα τους είναι πάνω στην διάμετρο του κύκλου ρ3, και οι δύο διάμετροι θα έχουν άθροισμα 10cm.Έτσι μπορούμε να φτιάξουμε την εξίσωση(για να βρούμε το χ):
$\frac{3x}{5}+\frac{6x}{15}=10$
μετά απο τις πράξεις βρίσκουμε χ=10.Άρα η διάμετρος του κύκλου ρ1 είναι:
$\frac{3x}{5}=\frac{3{\cdot}10}{5}=6cm$ και η ακτίνα του 3cm.Η διάμετρος του ρ2 είναι: $\frac{6x}{15}=\frac{6{\cdot}10}{15}=4cm$ και η ακτίνα του 2cm

β)Η περίμετος του ρ3 είναι:
L=2πρ=2π.5=10π=31,4.
Η περίμετρος του ρ2 είναι(μετά απο τις πράξεις):
L=12,56
Η περίμετρος του ρ1 είναι(μετά απο τις πράξεις):
L=18,84

γ) $\frac{6{\cdot}8}{2}=24cm^{2}$ .

δ)Το εμβαδόν του κύκλου ρ3 είναι:
$E=\pi \varrho ^{2}=5^{2}\pi =25\pi$
Το εμβαδόν του κύκλου ρ2 είναι(μετά απο τις πράξεις):
Ε=4π
Το εμβαδόν του κύκλου ρ1 είναι(μετά απο πράξεις):
Ε=9π
Προσθέτοντας τα εμβαδά των κύκλων ρ1 και ρ2 έχουμε 13π.Αφαιρόντας το 13π απο το εμβαδόν του μεγάλου κύκλου (ρ3) έχουμε:
25π-13π=12π. Άρα το εμβαδόν της κίτρινης επιφάνειας είναι 12π που είναι 37,68 τετραγ.εκατ.

ε)Η γωνία ΔΚΕ είναι 72 μοίρες διότι:είναι στο αντίστοιχο τόξο με τη γωνία Γ και ώς επίκεντρη πρέπει να είναι διπλάσια, άρα 72 μοίρες.Το εμβαδόν του κυκλικού τομέα ΔΚΕ είναι:
$E=\pi \varrho ^{2}{\cdot}\frac{\mu }{360}=3,14{\cdot}3^{2}{\cdot}\frac{72}{360}=\frac{2034,72}{360}=5,65cm^{2}$
Το τρίγωνο ΒΑΓ είναι ορθωγόνιο και αφού η γωνία Β είναι 36 μοίρες, η γωνία Α είναι 90 μοίρες, η γωνία Γ θα είναι 54 μοίρες.
Η γωνία ΕΜΖ είναι 108 μοίρες για τον ίδιο λόγο που εξήγησα παραπάνω.Άρα το εμβαδόν του κυκλικού τομέα ΜΖΕ είναι:
$E=\pi \varrho ^{2}{\cdot}\frac{\mu } {360}=3,14{\cdot}2^{2}{\cdot}\frac{108}{360}=\frac{1356,48}{360}=3,77cm^{2}$

#7

Μπράβο στα δύο κορίτσια που διαπραγματεύονται πολύ ωραία τις προτεινόμενες ασκήσεις.
Συνεχίζω με την

ΑΣΚΗΣΗ 4. Δίνεται ένα ημικύκλιο με διάμετρο ΑΒ και κέντρο Ο. Πάνω στο ημικύκλιο θεωρούμε τα σημεία Γ και Δ έτσι ώστε τα τόξα ΒΓ,ΓΔ και ΔΑ να είναι ίσα.
Αν η χορδή ΑΔ είναι 5cm,
(α) Να βρείτε το εμβαδόν του ημικύκλιου

(β) Να αποδείξετε ότι το τρίγωνο ΟΔΓ είναι ισόπλευρο

(γ) Να αποδείξετε ότι το τετράπλευρο ΑΒΓΔ είναι τραπέζιο

(δ) Να βρείτε το εμβαδόν του τραπεζίου ΑΒΓΔ

kritiman · #8

Γράφω εκ μέρους ενός φίλου μου

Υπάρχει η δυνατότητα να δούμε κάποιες ερωτήσεις θεωρίας για τα θέματα του θεωρητικού.
Και πάλι ευχαριστώ .

Αχ μακάρι όταν ήμουν εγω εδω να υπηρχαν site σαν το

ΔΗΜΗΤΡΙΟΣ ΚΑΤΣΙΠΟΔΑΣ · #9

Δες viewtopic.php?f=78&t=4172 ,υπάρχουν θεματα εξετάσεων παλαιοτερων ετων.
'Ωστε να δεις την δομή ενος διαγωνισματος.Επειδή εχει μειωθεί η ύλη ,καποια θέματα πιθανόν να είναι εκτος .

parmenides51 · #10

Δώρο το σχήμα

ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 4. Δίνεται ένα ημικύκλιο με διάμετρο ΑΒ και κέντρο Ο. Πάνω στο ημικύκλιο θεωρούμε τα σημεία Γ και Δ έτσι ώστε τα τόξα ΒΓ,ΓΔ και ΔΑ να είναι ίσα.
Αν η χορδή ΑΔ είναι 5cm,
(α) Να βρείτε το εμβαδόν του ημικύκλιου

(β) Να αποδείξετε ότι το τρίγωνο ΟΔΓ είναι ισόπλευρο

(γ) Να αποδείξετε ότι το τετράπλευρο ΑΒΓΔ είναι τραπέζιο

(δ) Να βρείτε το εμβαδόν του τραπεζίου ΑΒΓΔ

: ΑΣΚΗΣΗ 4..png (21.01 KiB) Προβλήθηκε 3843 φορές

#11

Επαναφορά (ξεχάστηκε...) . Αφορά μαθητές Β Γυμνασίου.

#12

ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:
ΑΣΚΗΣΗ 4. Δίνεται ένα ημικύκλιο με διάμετρο ΑΒ και κέντρο Ο. Πάνω στο ημικύκλιο θεωρούμε τα σημεία Γ και Δ έτσι ώστε τα τόξα ΒΓ,ΓΔ και ΔΑ να είναι ίσα.
Αν η χορδή ΑΔ είναι 5cm,
(α) Να βρείτε το εμβαδόν του ημικύκλιου

(β) Να αποδείξετε ότι το τρίγωνο ΟΔΓ είναι ισόπλευρο

(γ) Να αποδείξετε ότι το τετράπλευρο ΑΒΓΔ είναι τραπέζιο

(δ) Να βρείτε το εμβαδόν του τραπεζίου ΑΒΓΔ

Καλησπέρα.
α) Αφού τα τόξα είναι ίσα μεταξύ τους, θα είναι: $\displaystyle{{\rm A}\widehat {\rm O}\Delta = \Delta \widehat {\rm O}\Gamma = \Gamma \widehat {\rm O}{\rm A} = \frac{{{{180}^0}}}{3} = {60^0}}$

Στο ισοσκελές τρίγωνο $OA\Delta$ είναι: $\displaystyle{\Delta \widehat {\rm A}{\rm O} = {\rm A}\widehat \Delta {\rm O} = \frac{{{{180}^0} - {{60}^0}}}{2} = {60^0}}$ . Επομένως

το τρίγωνο είναι ισόπλευρο, δηλαδή η ακτἰνα του ημικυκλίου είναι $\boxed{R=5cm}$ .

Το εμβαδόν του ημικυκλίου είναι $\displaystyle{{\rm E} = \frac{1}{2}\pi {R^2} = \frac{{25\pi }}{2}c{m^2} \Leftrightarrow }$ $\boxed{E=39,25 cm^2}$

β) Από τα ίσα τόξα προκύπτει ότι και αντίστοιχες χορδές θα είναι ίσες, οπότε $A\Delta=\Delta\Gamma= O\Delta=O\Gamma=5cm$ . Άρα το τρίγωνο $O\Delta\Gamma$ είναι ισόπλευρο.

: AS-4.png (15.11 KiB) Προβλήθηκε 3297 φορές

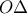γ) $\displaystyle{\Gamma \widehat \Delta {\rm O} = \Delta \widehat {\rm O}{\rm A} = {60^0} \Leftrightarrow \Gamma \Delta ||{\rm A}{\rm B}}$ (οι $AB, \Gamma\Delta$ τεμνόμενες από την $O\Delta$ σχηματίζουν τις εντός εναλλάξ γωνίες ίσες). Επειδή τώρα, $\displaystyle{\Gamma \Delta \ne {\rm A}{\rm B}}$ , το τετράπλευρο $AB\Gamma\Delta$ είναι τραπέζιο.

δ) Για να βρούμε το εμβαδόν του τραπεζίου χρειαζόμαστε το ύψος του

, δηλαδή το ύψος του ισοπλεύρου τριγώνου $AO\Delta$ .

$\displaystyle{\eta \mu {60^0} = \frac{\upsilon }{{{\rm O}\Delta }} \Leftrightarrow \upsilon = \frac{{5\sqrt 3 }}{2}}$

Άρα: $\displaystyle{({\rm A}{\rm B}\Gamma \Delta ) = \frac{{{\rm A}{\rm B} + \Gamma \Delta }}{2}\upsilon = \frac{{10 + 5}}{2} \cdot \frac{{5\sqrt 3 }}{2} \Leftrightarrow }$ $\boxed{({\rm A}{\rm B}\Gamma \Delta ) = \frac{{75\sqrt 3 }}{4}c{m^2}}$

: AS-4-d.png (4.66 KiB) Προβλήθηκε 3297 φορές

Ετοιμαζόμαστε για τις εξετάσεις

Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Re: Ετοιμαζόμαστε για τις εξετάσεις

Μέλη σε σύνδεση