Μια λύση με
Αναλυτική Γεωμετρία.
Να σημειώσω εδώ ότι, κατά τη γνώμη μου, πιο μεγάλη διδακτική αξία έχει η "προεργασία", δηλαδή η τοποθέτηση των σημείων στο σύστημα συντεταγμένων, ώστε να "μάς βολεύει" και λιγότερη η τεχνική της επίλυσης των συστημάτων, που μάς δίνουν τα υπόλοιπα σημεία και τις ζητούμενες συνθήκες.
Π.χ. δοκίμασα πρώτα το Α(0, 1), αλλά δεν βόλευε. Κατόπιν το C(1, 0), ούτε αυτό βόλευε... Μετά το Μ(1, 0) κι όλα έγινα πιο εύκολα!

- 09-6-2011 Γεωμετρία.jpg (20.98 KiB) Προβλήθηκε 1175 φορές
Σε ορθοκανονικό σύστημα συντεταγμένων με κέντρο

παίρνουμε σημεία

Στο ορθογώνιο τρίγωνο

είναι

.
Επίσης,

, οπότε Μ μέσο του ΒC και στο ορθογώνιο τρίγωνο

είναι

Οπότε

.
Το

είναι ορθογώνιο τρίγωνο με ύψος AD και διάμεσο AM.
Επίσης το S είναι συμμετρικό του D ως προς Β.
Ο κύκλος

με κέντρο Μ και ακτίνα MC έχει εξίσωση

(1)
Ο κύκλος

με κέντρο Β και ακτίνα ΒM έχει εξίσωση

(2)
Η κάθετη στoν x΄x στο S τέμνει τον

στα

Η ZC έχει εξίσωση:

Τέμνει τον

στα σημεία

Η DH έχει εξίσωση:

(3)
Οι συντεταγμένες του Τ επαληθεύουν την εξίσωση (3), οπότε το Τ ανήκει στην ευθεία που ορίζουν τα D, H.
Δεν δοκίμασα τη διερεύνηση που έκανε ο Στάθης στη δική του λύση.
 τρίγωνο
τρίγωνο  με
με  , ύψος
, ύψος  , και
, και  το μέσο της υποτείνουσας.
το μέσο της υποτείνουσας. και
και 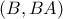 . Στο σημείο
. Στο σημείο  , που είναι συμμετρικό του
, που είναι συμμετρικό του  ως προς
ως προς  ,
,  . Η
. Η  (ξανα)τέμνει τον κύκλο
(ξανα)τέμνει τον κύκλο  στο σημείο
στο σημείο  .
. , είναι συνευθειακά .
, είναι συνευθειακά .
 τα οποία είναι ορθογώνια
τα οποία είναι ορθογώνια  , (υπόθεση)
, (υπόθεση)  (υπόθεση από τη συμμετρία) και
(υπόθεση από τη συμμετρία) και 
 άρα είναι ίσα οπότε:
άρα είναι ίσα οπότε:  και επειδή
και επειδή  συνευθειακά (από την υπόθεση) θα είναι και
συνευθειακά (από την υπόθεση) θα είναι και  συνευθειακά ( λόγω της ισότητας των
συνευθειακά ( λόγω της ισότητας των  ).
).  παραλληλόγραμμο οπότε
παραλληλόγραμμο οπότε 
 εγγράψιμο σε κύκλο (διαμέτρου
εγγράψιμο σε κύκλο (διαμέτρου  ) οπότε
) οπότε 
 μεσοκάθετη της
μεσοκάθετη της  (αφού
(αφού  απόστημα στη χορδή
απόστημα στη χορδή  συνευθειακά) η
συνευθειακά) η  άρα
άρα  .
.  (κάθετες στην ίδια ευθεία
(κάθετες στην ίδια ευθεία  και
και  ) οπότε το τετράπλευρο
) οπότε το τετράπλευρο  είναι ορθογώνιο άρα
είναι ορθογώνιο άρα  εντός εναλλάξ).
εντός εναλλάξ).  θα είναι
θα είναι  .
.  και επειδή έχουν κοινό σημείο το
και επειδή έχουν κοινό σημείο το  θα ισχύει
θα ισχύει  είναι συνευθειακά.
είναι συνευθειακά. η οποία δεν χρησιμοποιήθηκε στη λύση (το σχήμα έχει κατασκευαστεί και με αυτό το δεδομένο γι' αυτό φαίνεται ότι οι δύο (πράσινοι) κύκλοι είναι ίσοι)
η οποία δεν χρησιμοποιήθηκε στη λύση (το σχήμα έχει κατασκευαστεί και με αυτό το δεδομένο γι' αυτό φαίνεται ότι οι δύο (πράσινοι) κύκλοι είναι ίσοι) τέμνονται πάνω στον περιγεγραμμένο κύκλο του τριγώνου
τέμνονται πάνω στον περιγεγραμμένο κύκλο του τριγώνου 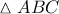 και φυσικά το σημείο τομής τους είναι και το μέσο του τμήματος
και φυσικά το σημείο τομής τους είναι και το μέσο του τμήματος 
 παίρνουμε σημεία
παίρνουμε σημεία 
 είναι
είναι  .
. , οπότε Μ μέσο του ΒC και στο ορθογώνιο τρίγωνο
, οπότε Μ μέσο του ΒC και στο ορθογώνιο τρίγωνο  είναι
είναι 
 .
.  είναι ορθογώνιο τρίγωνο με ύψος AD και διάμεσο AM.
είναι ορθογώνιο τρίγωνο με ύψος AD και διάμεσο AM. με κέντρο Μ και ακτίνα MC έχει εξίσωση
με κέντρο Μ και ακτίνα MC έχει εξίσωση  (1)
(1) με κέντρο Β και ακτίνα ΒM έχει εξίσωση
με κέντρο Β και ακτίνα ΒM έχει εξίσωση  (2)
(2)


 (3)
(3)



 εγγράψιμο ,άρα
εγγράψιμο ,άρα 
 ισοσκελές,
ισοσκελές,  άρα
άρα  μέσο
μέσο 








 επομένως τα
επομένως τα  είναι συνευθειακά
είναι συνευθειακά είναι εγγράψιμο και
είναι εγγράψιμο και 
 είναι ισοσκελές
είναι ισοσκελές 
 ,
,  και το τετράπλευρο
και το τετράπλευρο  εγγράψιμο
εγγράψιμο ανήκει στον περίκυκλο του τριγώνου
ανήκει στον περίκυκλο του τριγώνου  και
και 
 απόστημα της χορδής
απόστημα της χορδής  ...
...