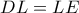Σελίδα 1 από 1
Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Δευ Αύγ 25, 2025 12:31 pm
από KARKAR
- Καθετότητα λόγω ομοιότητας.png (25.39 KiB) Προβλήθηκε 1096 φορές
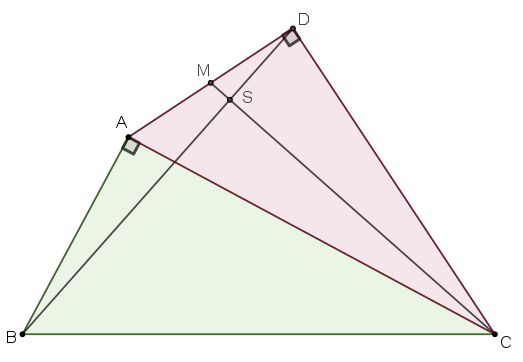
Με υποτείνουσα την κάθετη πλευρά

του ορθογωνίου τριγώνου

σχεδιάζουμε όμοιο τρίγωνο
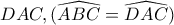
και ονομάζουμε

το μέσο της

. Δείξτε ότι :
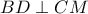
Re: Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Δευ Αύγ 25, 2025 2:23 pm
από Dimessi
Με

μέσο του

είναι
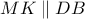
Από τις ομόλογες διαμέσους
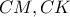
των
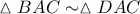
ισχύει
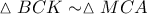
Από
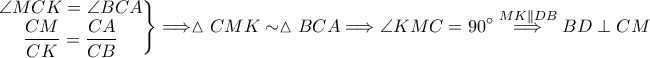
- Από παράλληλο.png (19.62 KiB) Προβλήθηκε 1073 φορές
Re: Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Δευ Αύγ 25, 2025 4:55 pm
από george visvikis
Dimessi έγραψε: ↑Δευ Αύγ 25, 2025 2:23 pm
Με

μέσο του

είναι
Από τις ομόλογες διαμέσους
των
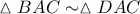
ισχύει
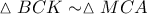
Από
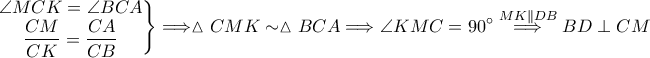
Από παράλληλο.png
Καλό 
Re: Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Δευ Αύγ 25, 2025 5:42 pm
από george visvikis
KARKAR έγραψε: ↑Δευ Αύγ 25, 2025 12:31 pm
Καθετότητα λόγω ομοιότητας.pngΜε υποτείνουσα την κάθετη πλευρά

του ορθογωνίου τριγώνου

σχεδιάζουμε όμοιο τρίγωνο
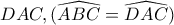
και ονομάζουμε

το μέσο της

. Δείξτε ότι :
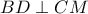
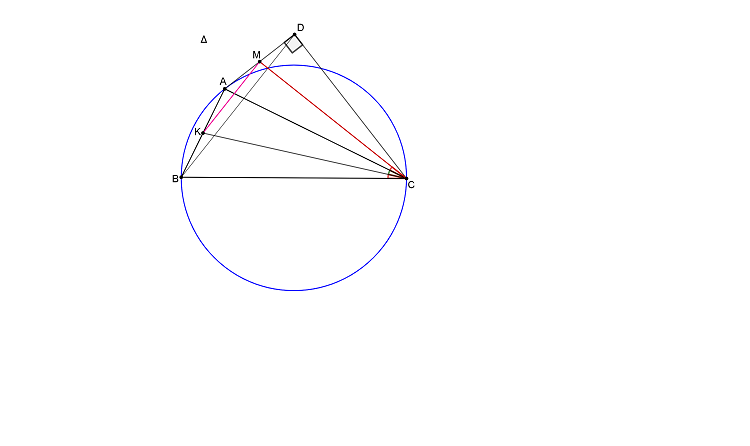
Αλλάζω λίγο την εκφώνηση. Θεωρώ

το σημείο τομής της

με το ημικύκλιο διαμέτρου

και

το σημείο τομής των
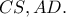
Θα δείξω ότι

είναι το μέσο της


- Καθετότητα-Ομοιότητα.png (17.65 KiB) Προβλήθηκε 1028 φορές
Οι μπλε γωνίες είναι ίσες, άρα η

εφάπτεται στο ημικύκλιο, οπότε
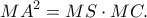
Αλλά από θεώρημα Ευκλείδη
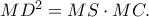
Επομένως
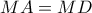
και το ζητούμενο αποδείχτηκε.
Re: Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Τρί Αύγ 26, 2025 10:19 am
από STOPJOHN
KARKAR έγραψε: ↑Δευ Αύγ 25, 2025 12:31 pm
Καθετότητα λόγω ομοιότητας.pngΜε υποτείνουσα την κάθετη πλευρά

του ορθογωνίου τριγώνου

σχεδιάζουμε όμοιο τρίγωνο
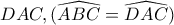
και ονομάζουμε

το μέσο της

. Δείξτε ότι :
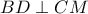
Από την ομοιότητα των τριγώνων
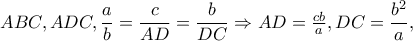
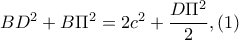
Από την ομοιότητα των τριγώνων
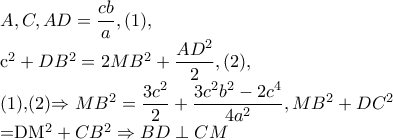
Re: Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Τρί Αύγ 26, 2025 3:37 pm
από ksofsa
Καθετότητα λόγω της ομοιότητας των χρωματισμένων τριγώνων.
Το

μέσο του

.
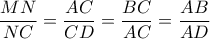
και

.
Άρα, το χρωματισμένα τρίγωνα όμοια και τα ζεύγη των ομόλογων πλευρών τους σχηματίζουν την ίδια γωνία, δηλαδή ορθή γωνία, αφού οι ομόλογες πλευρές
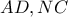
τέμνονται κάθετα.
Re: Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Τρί Αύγ 26, 2025 4:04 pm
από KARKAR
Έξοχη λύση αλλά η αξιοποίηση του τίτλου είναι θεόπνευστη

Re: Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Τρί Αύγ 26, 2025 10:03 pm
από Doloros
KARKAR έγραψε: ↑Δευ Αύγ 25, 2025 12:31 pm
Καθετότητα λόγω ομοιότητας.pngΜε υποτείνουσα την κάθετη πλευρά

του ορθογωνίου τριγώνου

σχεδιάζουμε όμοιο τρίγωνο
και ονομάζουμε

το μέσο της

. Δείξτε ότι :
Ας είναι

το μέσο του

. Θα είναι ,
. Έτσι τα τρίγωνα αυτά θα είναι ισογώνια.
Δηλαδή οι γωνίες με το ίδιο χρώμα είναι ίσες . Λόγω της ισότητας των γαλάζιων γωνιών,
.
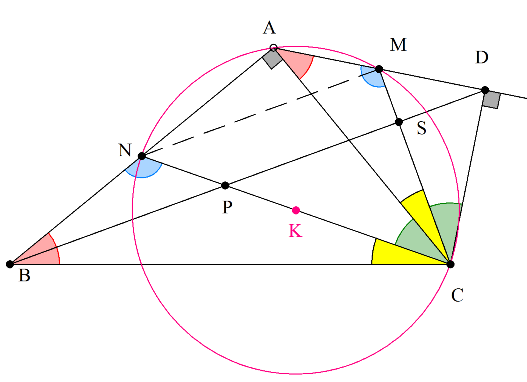
- Καθετότητα λόγω ομοιότητας_new.png (27.16 KiB) Προβλήθηκε 864 φορές
.
το τετράπλευρο
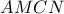
είναι εγγράψιμο σε κύκλο διαμέτρου
γιατί η
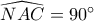
, οπότε και
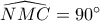
.
Αλλά
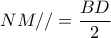
κι αφού
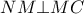
θα είναι και
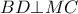
.
Παρατήρηση .
Όλες οι προηγούμενες λύσεις μου άρεσαν .
Εκ των υστέρων διαπιστώνω ότι η λύση μου ξεκινά με την ίδια σκέψη του
 αλλά με κάπως διαφορετική διαδρομή . την αφήνω .
αλλά με κάπως διαφορετική διαδρομή . την αφήνω .
Re: Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Πέμ Αύγ 28, 2025 12:07 pm
από Μιχάλης Τσουρακάκης
KARKAR έγραψε: ↑Δευ Αύγ 25, 2025 12:31 pm
Καθετότητα λόγω ομοιότητας.pngΜε υποτείνουσα την κάθετη πλευρά

του ορθογωνίου τριγώνου

σχεδιάζουμε όμοιο τρίγωνο
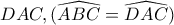
και ονομάζουμε

το μέσο της

. Δείξτε ότι :
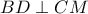
Μια λύση με χρήση εμβαδών..
Με

εγγράψιμμο
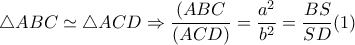
.Ακόμη
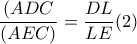
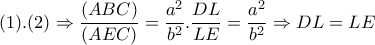
(αφού
)
Έτσι για τα όμοια τρίγωνα
είναι
Συνεπώς όλες οι κόκκινες γωνίες είναι ίσες (όπως και οι μπλε) και το
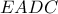
είναι εγγράψιμμος χαρταετός, άρα
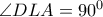
Είναι
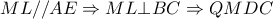
εγγράψιμμο ,άρα οι ροζ γωνίες είναι ίσες
Αλλά
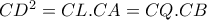
άρα η

εφάπτεται του κύκλου
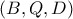
,επομένως η γωνία

είναι
επίσης ροζ,άρα
εγγράψιμμο,οπότε
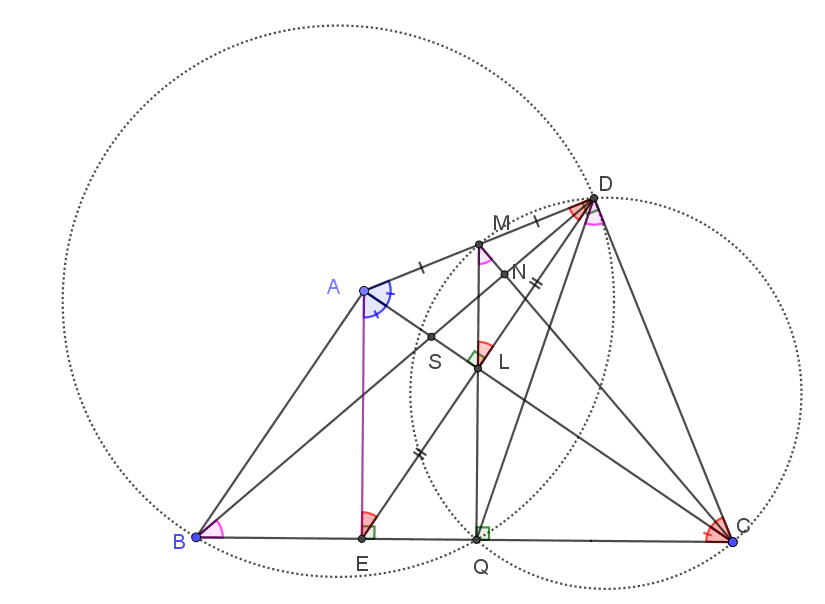
- καθετότητα λόγω ομοιότητας.png (44.01 KiB) Προβλήθηκε 781 φορές
Παρατήρηση
Στην παραπάνω λύση,ουσιαστικά αποδείχτηκε πρώτα ότι η γωνία

ισούται με τη γωνία

(Δεν πρόσεξα ότι αυτό δίνεται στην εκφώνηση)
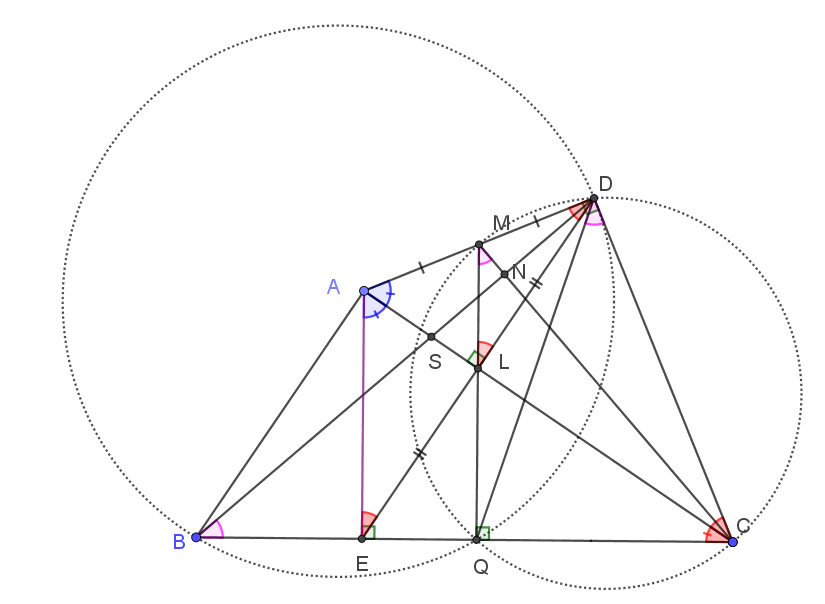
Στο παρακάτω σχήμα,είναι
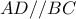
και οι γωνίες
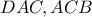
είναι ίσες ,άρα τα ορθογώνια τρίγωνα
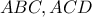
είναι επίσης όμοια
Όμως η γωνία
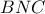
προφανώς είναι αμβλεία κι όχι ορθή πάντα
Ορθή είναι μόνο στην περίπτωση που το
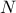
ταυτιστεί με το

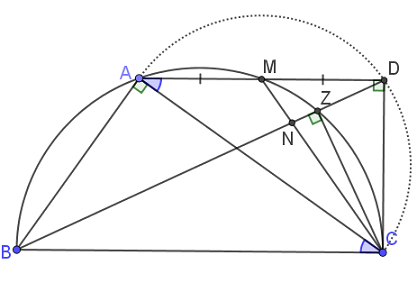
- καθετότητα....png (29.28 KiB) Προβλήθηκε 781 φορές
Re: Καθετότητα λόγω ομοιότητας
Δημοσιεύτηκε: Πέμ Αύγ 28, 2025 2:24 pm
από Μιχάλης Τσουρακάκης
KARKAR έγραψε: ↑Δευ Αύγ 25, 2025 12:31 pm
Καθετότητα λόγω ομοιότητας.pngΜε υποτείνουσα την κάθετη πλευρά

του ορθογωνίου τριγώνου

σχεδιάζουμε όμοιο τρίγωνο
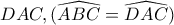
και ονομάζουμε

το μέσο της

. Δείξτε ότι :
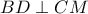
Λύση λαμβάνοντας υπ όψη την δεδομένη ισότητα γωνιών (που δεν πρόσεξα στην προηγούμενη ανάρτηση)
Με

εγγράψιμμο
Λόγω ισότητας των μπλε γωνιών το
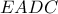
είναι εγγράψιμμος χαρταετός, άρα
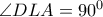
και προφανώς
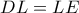
Είναι
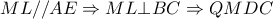
εγγράψιμμο ,άρα οι ροζ γωνίες είναι ίσες
Αλλά
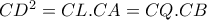
άρα η

εφάπτεται του κύκλου
,επομένως η γωνία

είναι επίσης ροζ,άρα
εγγράψιμμο,οπότε
- καθετότητα λόγω ομοιότητας.png (44.01 KiB) Προβλήθηκε 756 φορές
 του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου  σχεδιάζουμε όμοιο τρίγωνο
σχεδιάζουμε όμοιο τρίγωνο  και ονομάζουμε
και ονομάζουμε  το μέσο της
το μέσο της  . Δείξτε ότι :
. Δείξτε ότι : 
 του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου  σχεδιάζουμε όμοιο τρίγωνο
σχεδιάζουμε όμοιο τρίγωνο 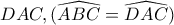 και ονομάζουμε
και ονομάζουμε  το μέσο της
το μέσο της  . Δείξτε ότι :
. Δείξτε ότι : 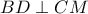
 μέσο του
μέσο του  είναι
είναι 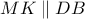
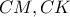 των
των 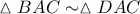 ισχύει
ισχύει 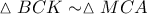
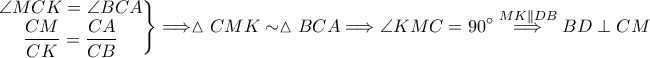
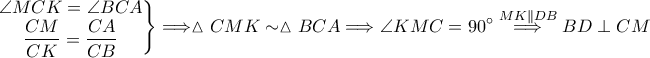
 το σημείο τομής της
το σημείο τομής της  με το ημικύκλιο διαμέτρου
με το ημικύκλιο διαμέτρου  και
και  Θα δείξω ότι
Θα δείξω ότι 
 εφάπτεται στο ημικύκλιο, οπότε
εφάπτεται στο ημικύκλιο, οπότε 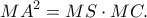
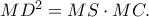 Επομένως
Επομένως 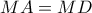 και το ζητούμενο αποδείχτηκε.
και το ζητούμενο αποδείχτηκε.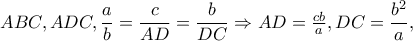
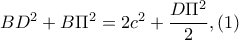
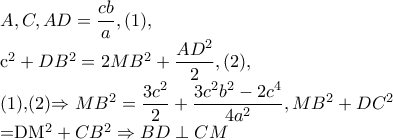
 μέσο του
μέσο του  .
.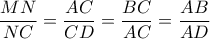 και
και .
.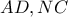 τέμνονται κάθετα.
τέμνονται κάθετα.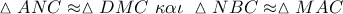 . Έτσι τα τρίγωνα αυτά θα είναι ισογώνια.
. Έτσι τα τρίγωνα αυτά θα είναι ισογώνια.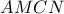 είναι εγγράψιμο σε κύκλο διαμέτρου
είναι εγγράψιμο σε κύκλο διαμέτρου 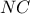 γιατί η
γιατί η 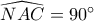 , οπότε και
, οπότε και 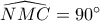 .
.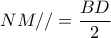 κι αφού
κι αφού 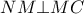 θα είναι και
θα είναι και 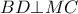 .
.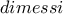 αλλά με κάπως διαφορετική διαδρομή . την αφήνω .
αλλά με κάπως διαφορετική διαδρομή . την αφήνω . εγγράψιμμο
εγγράψιμμο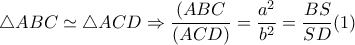 .Ακόμη
.Ακόμη 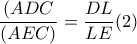
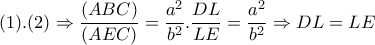 (αφού
(αφού 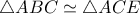 )
)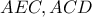 είναι
είναι 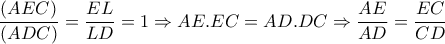
 είναι εγγράψιμμος χαρταετός, άρα
είναι εγγράψιμμος χαρταετός, άρα 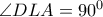
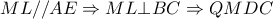 εγγράψιμμο ,άρα οι ροζ γωνίες είναι ίσες
εγγράψιμμο ,άρα οι ροζ γωνίες είναι ίσες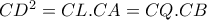 άρα η
άρα η 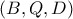 ,επομένως η γωνία
,επομένως η γωνία  είναι
είναι 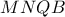 εγγράψιμμο,οπότε
εγγράψιμμο,οπότε 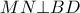

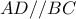 και οι γωνίες
και οι γωνίες 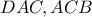 είναι ίσες ,άρα τα ορθογώνια τρίγωνα
είναι ίσες ,άρα τα ορθογώνια τρίγωνα 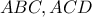 είναι επίσης όμοια
είναι επίσης όμοια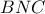 προφανώς είναι αμβλεία κι όχι ορθή πάντα
προφανώς είναι αμβλεία κι όχι ορθή πάντα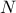 ταυτιστεί με το
ταυτιστεί με το