 του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου  σχεδιάζουμε όμοιο τρίγωνο
σχεδιάζουμε όμοιο τρίγωνο 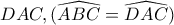 και ονομάζουμε
και ονομάζουμε  το μέσο της
το μέσο της  . Δείξτε ότι :
. Δείξτε ότι : 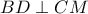
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου  σχεδιάζουμε όμοιο τρίγωνο
σχεδιάζουμε όμοιο τρίγωνο 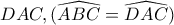 και ονομάζουμε
και ονομάζουμε  το μέσο της
το μέσο της  . Δείξτε ότι :
. Δείξτε ότι : 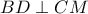
Αλλάζω λίγο την εκφώνηση. Θεωρώ
 το σημείο τομής της
το σημείο τομής της  με το ημικύκλιο διαμέτρου
με το ημικύκλιο διαμέτρου  και
και  το σημείο τομής των
το σημείο τομής των 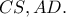 Θα δείξω ότι
Θα δείξω ότι  είναι το μέσο της
είναι το μέσο της  Οι μπλε γωνίες είναι ίσες, άρα η
Οι μπλε γωνίες είναι ίσες, άρα η  εφάπτεται στο ημικύκλιο, οπότε
εφάπτεται στο ημικύκλιο, οπότε 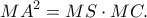
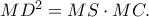 Επομένως
Επομένως 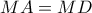 και το ζητούμενο αποδείχτηκε.
και το ζητούμενο αποδείχτηκε.Από την ομοιότητα των τριγώνων
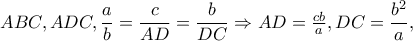
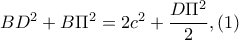
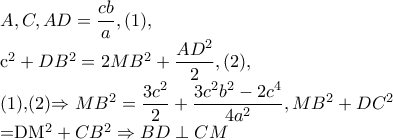
 μέσο του
μέσο του  .
.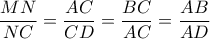 και
και .
.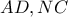 τέμνονται κάθετα.
τέμνονται κάθετα.Ας είναι
 το μέσο του
το μέσο του  . Θα είναι ,
. Θα είναι , 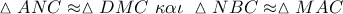 . Έτσι τα τρίγωνα αυτά θα είναι ισογώνια.
. Έτσι τα τρίγωνα αυτά θα είναι ισογώνια.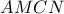 είναι εγγράψιμο σε κύκλο διαμέτρου
είναι εγγράψιμο σε κύκλο διαμέτρου 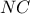 γιατί η
γιατί η 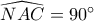 , οπότε και
, οπότε και 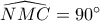 .
.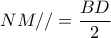 κι αφού
κι αφού 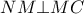 θα είναι και
θα είναι και 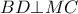 .
.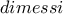 αλλά με κάπως διαφορετική διαδρομή . την αφήνω .
αλλά με κάπως διαφορετική διαδρομή . την αφήνω .Μια λύση με χρήση εμβαδών..
 εγγράψιμμο
εγγράψιμμο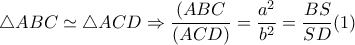 .Ακόμη
.Ακόμη 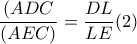
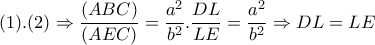 (αφού
(αφού 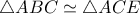 )
)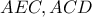 είναι
είναι 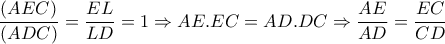
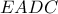 είναι εγγράψιμμος χαρταετός, άρα
είναι εγγράψιμμος χαρταετός, άρα 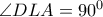
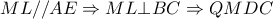 εγγράψιμμο ,άρα οι ροζ γωνίες είναι ίσες
εγγράψιμμο ,άρα οι ροζ γωνίες είναι ίσες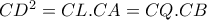 άρα η
άρα η  εφάπτεται του κύκλου
εφάπτεται του κύκλου 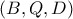 ,επομένως η γωνία
,επομένως η γωνία  είναι
είναι 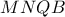 εγγράψιμμο,οπότε
εγγράψιμμο,οπότε 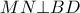
 ισούται με τη γωνία
ισούται με τη γωνία 
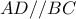 και οι γωνίες
και οι γωνίες 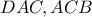 είναι ίσες ,άρα τα ορθογώνια τρίγωνα
είναι ίσες ,άρα τα ορθογώνια τρίγωνα 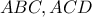 είναι επίσης όμοια
είναι επίσης όμοια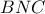 προφανώς είναι αμβλεία κι όχι ορθή πάντα
προφανώς είναι αμβλεία κι όχι ορθή πάντα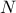 ταυτιστεί με το
ταυτιστεί με το 
Λύση λαμβάνοντας υπ όψη την δεδομένη ισότητα γωνιών (που δεν πρόσεξα στην προηγούμενη ανάρτηση)
 εγγράψιμμο
εγγράψιμμο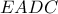 είναι εγγράψιμμος χαρταετός, άρα
είναι εγγράψιμμος χαρταετός, άρα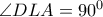 και προφανώς
και προφανώς 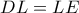
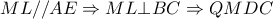 εγγράψιμμο ,άρα οι ροζ γωνίες είναι ίσες
εγγράψιμμο ,άρα οι ροζ γωνίες είναι ίσες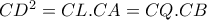 άρα η
άρα η  εφάπτεται του κύκλου
εφάπτεται του κύκλου 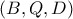 ,επομένως η γωνία
,επομένως η γωνία 
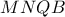 εγγράψιμμο,οπότε
εγγράψιμμο,οπότε 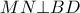
Μέλη σε αυτήν τη Δ. Συζήτηση: SemrushBot και 2 επισκέπτες