 , αν ικανοποιεί τις παρακάτω εξισώσεις
, αν ικανοποιεί τις παρακάτω εξισώσεις
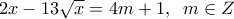
Συντονιστές: achilleas, emouroukos, silouan
 , αν ικανοποιεί τις παρακάτω εξισώσεις
, αν ικανοποιεί τις παρακάτω εξισώσεις
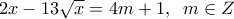



 και επομένως για να έχει λύση η εξίσωση πρέπει
και επομένως για να έχει λύση η εξίσωση πρέπει 
 συμπεραίνουμε ότι και
συμπεραίνουμε ότι και 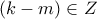
 με
με 

 ) είναι:
) είναι:  και άρα
και άρα
 γρήγορα καταλήγουμε σε μια αδύνατη εξίσωση.
γρήγορα καταλήγουμε σε μια αδύνατη εξίσωση.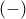 έχουμε:
έχουμε:
 με
με 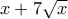 οπότε:
οπότε:
 από την οποία εύκολα προκύπτει οτι
από την οποία εύκολα προκύπτει οτι  ή
ή  οι οποίες είναι δεκτές λύσεις.
οι οποίες είναι δεκτές λύσεις. προκύπτει όταν
προκύπτει όταν 

Δεν μου φαίνεται και πολύ προφανές αυτό το κομμάτι, πως καταλήγεις σε αδύνατη εξίσωση;
Το ότι το μηδέν δεν μπορεί να είναι λύση φαίνεται εύκολα αν το αντικαταστήσεις στο αρχικό σύστημα. Το πρώτο μέλος των εξισώσεων θα είναι ίσο με μηδέν ενώ το δεύτερο δεν μπορεί να είναι ποτέ μηδέν.
Αν δεν έχω κάνει κάπου λάθος στην πρώτη εξίσωση καταλήγω σε άθροισμα ριζών που ισούται με αρνητικό αριθμό.Al.Koutsouridis έγραψε: ↑Πέμ Ιούλ 05, 2018 10:19 amΔεν μου φαίνεται και πολύ προφανές αυτό το κομμάτι, πως καταλήγεις σε αδύνατη εξίσωση;
Το ότι το μηδέν δεν μπορεί να είναι λύση φαίνεται εύκολα αν το αντικαταστήσεις στο αρχικό σύστημα. Το πρώτο μέλος των εξισώσεων θα είναι ίσο με μηδέν ενώ το δεύτερο δεν μπορεί να είναι ποτέ μηδέν.

Η αλήθεια είναι δεν έχω κάνει τις πράξεις που αναφαίρεις, οπότε δεν ξέρω αν είναι σωστές και υπάρχουν λογικά κενά.Chagi έγραψε: ↑Πέμ Ιούλ 05, 2018 10:44 am
Αν δεν έχω κάνει κάπου λάθος στην πρώτη εξίσωση καταλήγω σε άθροισμα ριζών που ισούται με αρνητικό αριθμό.
Όσο για το γεγονός ότι δέχτηκα τη λύση
Αλλά αυτά παθαίνει κάποιος όταν δεν επαληθεύει.
Από περιέργεια υπάρχει πιο γρήγορος τρόπος που οδηγεί στην επίλυση της άσκησης;
Σας ευχαριστώ!
 θα δεις οτι υπάρχουν ακέραιοι
θα δεις οτι υπάρχουν ακέραιοι  που επαληθεύουν το σύστημα.
που επαληθεύουν το σύστημα. 

 . Άρα
. Άρα 
 με
με  και
και 

 . 'Αρα υπάρχει
. 'Αρα υπάρχει  με
με  . Άρα
. Άρα  , οπότε
, οπότε  ή
ή  . Άρα υπάρχει
. Άρα υπάρχει  με
με  . Η δεύτερη σχέση του συστήματος γράφεται:
. Η δεύτερη σχέση του συστήματος γράφεται:  . Δουλεύοντας με
. Δουλεύοντας με  έχουμε
έχουμε  . Άρα
. Άρα  . Στις αρχικές σχέσεις δουλεύοντας με
. Στις αρχικές σχέσεις δουλεύοντας με  βλέπουμε ότι επαληθεύονται μόνο με
βλέπουμε ότι επαληθεύονται μόνο με  . Άρα πρέπει και αρκεί να υπάρχει
. Άρα πρέπει και αρκεί να υπάρχει  με
με 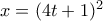 . edit: μικρή διόρθωση.
. edit: μικρή διόρθωση.sov_arvyd έγραψε: ↑Πέμ Ιούλ 05, 2018 6:47 pmΈστω
Έχουμε:
Με αφαίρεση κατά μέλη έχουμε:
. Άρα
Έστωμε
και
Έχουμε:
Με πρόσθεση κατά μέλη:. 'Αρα υπάρχει
με
. Άρα
, οπότε
ή
. Άρα υπάρχει
με
. Η δεύτερη σχέση του συστήματος γράφεται:
. Δουλεύοντας με
έχουμε
. Άρα
. Στις αρχικές σχέσεις δουλεύοντας με
βλέπουμε ότι επαληθεύονται μόνο με
. Άρα πρέπει και αρκεί να υπάρχει
με
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες