Η αναζήτηση βρήκε 979 εγγραφές
Επιστροφή στην ειδική αναζήτηση
- Παρ Ιουν 06, 2025 10:49 am
- Δ. Συζήτηση: Ανάλυση
- Θέμα: Άνω και κάτω φράγμα εμβαδού
- Απαντήσεις: 4
- Προβολές: 2405
Re: Άνω και κάτω φράγμα εμβαδού
Με αφορμή το θέμα εδώ , προτείνουμε προς απόδειξη τη διπλή ανισότητα: $\dfrac{e^2-1}{2\sqrt[4]{e}}<E<\dfrac{e^2-1}{2}$. Το άνω φράγμα έχει προταθεί και αποδειχθεί στην παραπομπή. Με το παρόν μήνυμα προτείνουμε το κάτω φράγμα, για το οποίο δε διαθέτουμε ακόμα λύση με σχολικά μέσα. Ας σημειώσουμε ότι...
- Τρί Ιουν 04, 2024 12:14 am
- Δ. Συζήτηση: Πανελλήνιες Εξετάσεις
- Θέμα: Θέματα Πανελληνίων εξετάσεων ΕΠΑΛ 2024
- Απαντήσεις: 20
- Προβολές: 6188
Re: Θέματα Πανελληνίων εξετάσεων ΕΠΑΛ 2024
Παρακάτω στο Γ3 δεν γίνεται να προκύψει άλλη λύση εκτός του 10. Έχει προηγηθεί το Γ2 και έχει δωθεί η απάντηση. Δεν βγαίνει άλλη τιμή και δεν υπάρχει λόγος να υπάρξει "διεύρυνση" στις οδηγίες διόρθωσης. Ναι, αλλά στην προσπάθεια να υπολογίσουμε το κ, αν αντί να ξεκινήσουμε από την $x=20$ ξεκινήσουμ...
- Σάβ Ιουν 01, 2024 4:04 pm
- Δ. Συζήτηση: Πανελλήνιες Εξετάσεις
- Θέμα: Θέματα Πανελληνίων εξετάσεων ΕΠΑΛ 2024
- Απαντήσεις: 20
- Προβολές: 6188
Re: Θέματα Πανελληνίων εξετάσεων ΕΠΑΛ 2024
Νομίζω ότι το θέμα Γ είναι προβληματικό.
Από τη μία, το κ μπορεί να πάρει και αρνητική τιμή, μια πολύ αρνητική μεν όπου δεν μπορεί να προκύψει λογική θερμοκρασία για πόλη της Ελλάδας. Από την άλλη, το που θέλουμε να είναι ίσο το όριο εξακολουθεί να στέκει;
που θέλουμε να είναι ίσο το όριο εξακολουθεί να στέκει;
Από τη μία, το κ μπορεί να πάρει και αρνητική τιμή, μια πολύ αρνητική μεν όπου δεν μπορεί να προκύψει λογική θερμοκρασία για πόλη της Ελλάδας. Από την άλλη, το
 που θέλουμε να είναι ίσο το όριο εξακολουθεί να στέκει;
που θέλουμε να είναι ίσο το όριο εξακολουθεί να στέκει;- Κυρ Απρ 23, 2023 6:58 pm
- Δ. Συζήτηση: Γενικά Μηνύματα
- Θέμα: Χρόνια Πολλά στους Γεώργιους
- Απαντήσεις: 16
- Προβολές: 1947
Re: Χρλινια Πολλά στους Γεώργιους
Ευχές για υγεία και ευτυχία σε όλους τους εορτάζοντες.
Να είστε καλά, κύριοι
Βισβίκη, Μπαλόγλου, Ρίζο.
Να είστε καλά, κύριοι
Βισβίκη, Μπαλόγλου, Ρίζο.
- Δευ Απρ 17, 2023 2:23 pm
- Δ. Συζήτηση: Γενικά Μηνύματα
- Θέμα: ΕΥΧΕΣ ΑΝΑΣΤΑΣΗΣ
- Απαντήσεις: 8
- Προβολές: 1273
Re: ΕΥΧΕΣ ΑΝΑΣΤΑΣΗΣ
Χριστός Ανέστη,
πολλές ευχές για υγεία και ευτυχία σε όλους!
πολλές ευχές για υγεία και ευτυχία σε όλους!
- Δευ Αύγ 01, 2022 1:00 pm
- Δ. Συζήτηση: ΘΕΜΑΤΑ ΜΕ ΑΠΑΙΤΗΣΕΙΣ Γ'
- Θέμα: Σύνολο τιμων
- Απαντήσεις: 1
- Προβολές: 1646
Re: Σύνολο τιμων
Θα παρακαλούσα τον θεματοδότη Λάμπρο Κατσάπα να γράψει τη λύση, αν δεν του είναι κόπος.
Έστω και να μου την περιγράψει σε προσωπικό μήνυμα.
Έστω και να μου την περιγράψει σε προσωπικό μήνυμα.
- Τετ Ιούλ 13, 2022 2:54 pm
- Δ. Συζήτηση: Γενικά Μηνύματα
- Θέμα: Τηλεσκόπιο James Webb
- Απαντήσεις: 5
- Προβολές: 1080
Re: Τηλεσκόπιο James Webb
Ζούμε κοσμοϊστορικές στιγμές. Το πιστεύω αυτό και μαζί κάθε άνθρωπος με λίγη νόηση. Είναι θέματα με τα οποία θα ασχοληθεί ο ιστορικός του μέλλοντος. Ας μου επιτραπεί να προτείνω το κανάλι του Παύλου Καστανά. Είναι πιο λαϊκό και προσωπικά δηλώνω φαν. https://m.youtube.com/watch?v=UMGobvktfuM Δεν ξέρω...
- Παρ Ιουν 17, 2022 11:56 pm
- Δ. Συζήτηση: ΑΛΓΕΒΡΑ Β'
- Θέμα: Εκθετικές εξισώσεις
- Απαντήσεις: 3
- Προβολές: 958
Re: Εκθετικές εξισώσεις
Για το (β), για να μη μένει.. Έχουμε δείξει στην (α) και εγώ και ακόμη πιο λιτά ο KARKAR ότι $4^{x}9^{\frac{1}{x}}+9^{x}4^{\frac{1}{x}} \geq 72$, με την ισότητα να ισχύει μόνο για $x=1$. Επιπλέον, ισχύει $6^{x+\frac{1}{x}} \geq 6^{2}=36$, με την ισότητα να ισχύει και πάλι μόνο για $x=1$. Άρα, $4^{x}...
- Παρ Ιουν 17, 2022 4:51 pm
- Δ. Συζήτηση: Διασκεδαστικά Μαθηματικά
- Θέμα: "Γνωστές" ρίζες
- Απαντήσεις: 7
- Προβολές: 1510
Re: "Γνωστές" ρίζες
Επίσης, από τον λογαριθμικό μέσο, έχουμε
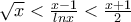 , για
, για  .
.
Για :
: 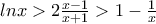 .
.
Για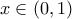 :
:  .
.
Ελπίζω να μην το παρακάνουμε..
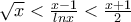 , για
, για  .
.Για
 :
: 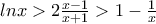 .
.Για
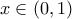 :
:  .
.Ελπίζω να μην το παρακάνουμε..
- Παρ Ιουν 17, 2022 3:05 pm
- Δ. Συζήτηση: ΑΛΓΕΒΡΑ Β'
- Θέμα: Εκθετικές εξισώσεις
- Απαντήσεις: 3
- Προβολές: 958
Re: Εκθετικές εξισώσεις
Για την (α) Αρχικά, η εξίσωση είναι αδύνατη στο $(- \infty,0]$ διότι $4^{x}9^{\frac{1}{x}} \leq 1$ και $9^{x}4^{\frac{1}{x}} \leq 1$. Επιπλέον, αν η εξίσωση έχει ρίζα $k$ στο $(1,+ \infty)$, θα έχει προφανώς και την $\frac{1}{k} \in (0,1)$. Υπάρχει η παρατηρούμενη ρίζα $x=1$ και θα αποδείξουμε ότι ε...
- Παρ Ιουν 17, 2022 1:40 pm
- Δ. Συζήτηση: Άλγεβρα - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Τριγωνομετρική ταυτότητα από ταυτότητα.
- Απαντήσεις: 1
- Προβολές: 637
Re: Τριγωνομετρική ταυτότητα από ταυτότητα.
$sin5xsin9x=sin4xsin16x \Rightarrow$ $sin\frac{14x-4x}{2}sin\frac{14x+4x}{2} = sin\frac{20x-12x}{2}sin\frac{20x+12x}{2} \Rightarrow$ $cos14x -cos4x =cos20x - cos12x \Rightarrow$ $cos20x-cos14x=cos12x-cos4x \Rightarrow$ $-2sin\frac{34x}{2}sin\frac{6x}{2}=-2sin\frac{16x}{2}sin\frac{8x}{2} \Rightarrow$...
- Παρ Ιουν 17, 2022 12:12 am
- Δ. Συζήτηση: Διασκεδαστικά Μαθηματικά
- Θέμα: "Γνωστές" ρίζες
- Απαντήσεις: 7
- Προβολές: 1510
Re: "Γνωστές" ρίζες
Μια ακόμη,
Για ,
,

Για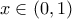

Για , ισχύει η ισότητα.
, ισχύει η ισότητα.
Για
 ,
,
Για
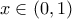

Για
 , ισχύει η ισότητα.
, ισχύει η ισότητα.- Δευ Ιουν 13, 2022 4:04 pm
- Δ. Συζήτηση: Διασκεδαστικά Μαθηματικά
- Θέμα: "Γνωστές" ρίζες
- Απαντήσεις: 7
- Προβολές: 1510
Re: "Γνωστές" ρίζες
Γεια σας , για το δεύτερο ερώτημα, για το οποίο υπάρχουν θετικά $x_{1},x_{2}$, με $x_{1}<x_{2}$ τέτοια, ώστε $e^{x_{1}}=3x_{1} \Leftrightarrow ln(3x_{1})=x_{1} \Leftrightarrow lnx_{1}=x_{1}-ln3$ και $e^{x_{2}}=3x_{2} \Leftrightarrow ln(3x_{2})=x_{2} \Leftrightarrow lnx_{2}=x_{2}-ln3$, είναι $lnx \ge...
- Κυρ Ιουν 12, 2022 12:21 am
- Δ. Συζήτηση: ΘΕΜΑΤΑ ΜΕ ΑΠΑΙΤΗΣΕΙΣ Γ'
- Θέμα: Κοινή εφαπτομένη
- Απαντήσεις: 2
- Προβολές: 1429
Re: Κοινή εφαπτομένη
Ενδιαφέρον! Έστω $a\in (1,e)$ η μοναδική λύση της εξίσωσης $lnx=\frac{1}{x}.$ Τότε $\displaystyle{f(a)=g(a).}$ Επιπλέον η $f-g$ παρουσιάζει ελάχιστο στο $a$ οπότε δεν έχουμε άλλη λύση και βέβαια $f'(a)=g'(a).$ Η πρώτη ανισότητα είναι τώρα προφανής από κυρτότητα. Για την δεύτερη Η συνάρτηση $\displa...
- Παρ Ιουν 10, 2022 12:52 pm
- Δ. Συζήτηση: ΘΕΜΑΤΑ ΜΕ ΑΠΑΙΤΗΣΕΙΣ Γ'
- Θέμα: Κοινή εφαπτομένη
- Απαντήσεις: 2
- Προβολές: 1429
Κοινή εφαπτομένη
Δίνονται οι συναρτήσεις $f,g:(1,+ \infty) \rightarrow R$ , με $f(x)=(x-1)lnx$ και $g(x)=ln(lnx)+1$ , για κάθε $x>1$. Α. Να αποδείξετε ότι η $f$ είναι κυρτή και η $g$ είναι κοίλη στο $(1,+ \infty)$. Β. Να αποδείξετε ότι οι $C_{f},C_{g}$ έχουν σε κοινό τους σημείο, με τετμημένη $a \in (1,e)$, κοινή εφ...
- Κυρ Μάιος 08, 2022 9:01 pm
- Δ. Συζήτηση: ΘΕΜΑΤΑ ΜΕ ΑΠΑΙΤΗΣΕΙΣ Γ'
- Θέμα: Ολοκλήρωμα - Ανισότητα
- Απαντήσεις: 1
- Προβολές: 1202
Ολοκλήρωμα - Ανισότητα
Να αποδείξετε ότι


- Πέμ Μαρ 10, 2022 12:09 am
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Δυσκολούτσικη συναρτησιακή
- Απαντήσεις: 5
- Προβολές: 3424
Re: Δυσκολούτσικη συναρτησιακή
Έφυγα για τσιγάρα και δραπέτευσα στη Βραζιλία. 
Πώς πέρασαν 7 χρόνια!
Θα συνέχιζα, αλλά δεν έχω κουράγιο..
Πώς πέρασαν 7 χρόνια!
Θα συνέχιζα, αλλά δεν έχω κουράγιο..
- Πέμ Μαρ 10, 2022 12:00 am
- Δ. Συζήτηση: ΘΕΜΑΤΑ ΜΕ ΑΠΑΙΤΗΣΕΙΣ Γ'
- Θέμα: Ημιτριγωνομετρική ανισότητα
- Απαντήσεις: 6
- Προβολές: 1484
Re: Ημιτριγωνομετρική ανισότητα
Να δειχθεί ότι ισχύει η $x^2\leq sinxtanx$ για $-\dfrac{\pi}{2}<x<\dfrac{\pi}{2}$. Καλημέρα σας. Η προσπάθειά μου. Θα δουλέψω με τη συνάρτηση $f(x)=\frac{sinx}{\sqrt{cosx}}-x$ στο $[0,\frac{\pi}{2})$. Στο $(0,\frac{\pi}{2})$, είναι $f'(x)=\frac{cosx \cdot \sqrt{cosx}+\frac{sin^{2}x}{2 \sqrt{cosx}}}...
- Σάβ Νοέμ 20, 2021 6:52 pm
- Δ. Συζήτηση: ΑΛΓΕΒΡΑ Β'
- Θέμα: Τριγωνομετρικό-εκθετική εξίσωση με παράμετρο
- Απαντήσεις: 2
- Προβολές: 793
Re: Τριγωνομετρικό-εκθετική εξίσωση με παράμετρο
Η $g(x)=sin(\frac{\pi}{6}+\pi^{1-x^{2}})$ είναι άρτια στο $R$ και παρουσιάζει ολικό ελάχιστο ΜΟΝΑΔΙΚΑ στη θέση $x=0$, το $g(0)=sin \frac{7 \pi}{6}=- \frac{1}{2}$. Πράγματι, $1-x^{2} \leq 1 \Leftrightarrow 0 < \pi^{1-x^{2}} \leq \pi \Leftrightarrow \frac{\pi}{6} <\frac{\pi}{6}+\pi^{1-x^{2}} \leq \fra...
- Κυρ Νοέμ 14, 2021 12:58 pm
- Δ. Συζήτηση: ΑΛΓΕΒΡΑ Β'
- Θέμα: Ανίσωση
- Απαντήσεις: 1
- Προβολές: 684
Re: Ανίσωση
Γεια σας, καλημέρα. Η προσπάθειά μου για την όμορφη ανίσωση. Δουλεύουμε φυσικά για $x>0$. Ισοδύναμα, $2x^{2}+4(2x-7)^{3} \leq x \sqrt{x}+7x \Leftrightarrow$ $x(2x-7)+4(2x-7)^{3} \leq x \sqrt{x} \Leftrightarrow$ $(2x-7)[x+4(2x-7)^{2}] \leq x \sqrt{x} \Leftrightarrow$ $\frac{2x-7}{\sqrt{x}}[4(\frac{2x...
