Η αναζήτηση βρήκε 6232 εγγραφές
Επιστροφή στην ειδική αναζήτηση
- Κυρ Αύγ 18, 2024 1:52 pm
- Δ. Συζήτηση: Άλγεβρα - Προχωρημένο Επίπεδο (Juniors)
- Θέμα: Ανισότητα απ' ανισότητα
- Απαντήσεις: 2
- Προβολές: 1942
Re: Ανισότητα απ' ανισότητα
Θεωρώ τον μιγαδικό $\displaystyle{z=(a+i)(b+2i)(c+3i),}$ για τον οποίο δίνεται ότι $\displaystyle{z\bar{z}\leq 100}$. Είναι $\displaystyle{z=(abc-6a-3b-2c)+(3ab+2ac+bc-6)i}$, οπότε $\displaystyle{z\bar{z}=(abc-6a-3b-2c)^2+(3ab+2ac+bc-6)^2}$. Επομένως έχουμε $\displaystyle{(abc-6a-3b-2c)^2+(3ab+2ac+b...
- Κυρ Ιουν 16, 2024 12:41 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Ένα άθροισμα!
- Απαντήσεις: 1
- Προβολές: 662
Re: Ένα άθροισμα!
Να υπολογιστεί το άθροισμα $\displaystyle{\sum_{n=1}^{\infty} \frac{3^n \cdot 5^n}{\left ( 5^n - 3^n \right ) \left ( 5^{n+1} - 3^{n+1} \right )}}$. Ισχύει $\displaystyle{ \frac{3^n \cdot 5^n}{\left ( 5^n - 3^n \right ) \left ( 5^{n+1} - 3^{n+1} \right )}=\frac{1}{2}\left(\frac{5^n}{5^n-3^n}-\frac{...
- Κυρ Ιουν 16, 2024 12:30 am
- Δ. Συζήτηση: ΑΛΓΕΒΡΑ Α'
- Θέμα: Μία ρίζα
- Απαντήσεις: 4
- Προβολές: 968
Re: Μία ρίζα
Το υπόρριζο είναι το
 , για
, για  , οπότε
, οπότε


Άρα ο αριθμός ισούται με .
.
 , για
, για  , οπότε
, οπότε

Άρα ο αριθμός ισούται με
 .
.- Δευ Μάιος 20, 2024 12:05 am
- Δ. Συζήτηση: ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β'
- Θέμα: Δύο απ' αυτά είναι αντίρροπα
- Απαντήσεις: 4
- Προβολές: 1246
Re: Δύο απ' αυτά είναι αντίρροπα
Αλλιώς: Το ζητούμενο μεταφράζεται στο εξής: Αν $\displaystyle{x=\angle (\vec{a},\vec{b}), y=\angle (\vec{b},\vec{c}), z=\angle (\vec{c},\vec{a})}$ $\displaystyle{x+y+z=2\pi \wedge \cos x+\cos y+\cos z=-1\implies x+y=\pi \lor y+z=\pi \lor z+x=\pi}$. Αυτό είναι άμεσο από την ταυτότητα $\displaystyle{\...
- Κυρ Μάιος 12, 2024 9:10 pm
- Δ. Συζήτηση: Άλγεβρα - Προχωρημένο Επίπεδο (Seniors)
- Θέμα: Κλάσματα πολυώνυμων
- Απαντήσεις: 3
- Προβολές: 2283
Re: Κλάσματα πολυώνυμων
Θα ήθελα να ευχαριστήσω τον Ιάσωνα για την λύση και το χρόνο του. Για την ιστορία η άσκηση είναι από την ολυμπιάδα "Υψηλά πρότυπα" για το έτος 2021/22 , του πανεπιστημίου Ανώτατη Σχολή Οικονομικών (Ρωσία). Ενδιαφέρον, δεδομένου ότι το 2006 σε τεστ επιλογής της Βουλγαρίας για την Διεθνή Μαθηματική Ο...
- Πέμ Απρ 11, 2024 6:14 pm
- Δ. Συζήτηση: Ανάλυση
- Θέμα: Αναπόδεικτο λήμμα
- Απαντήσεις: 1
- Προβολές: 757
Re: Αναπόδεικτο λήμμα
Στην πραγματικότητα είναι το εξής:
Αν η είναι κυρτή στο
είναι κυρτή στο ![\displaystyle{[a,b]} \displaystyle{[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/14f53999651f504e8f7c5c1b74530f3e.png) τότε το μέγιστό της είναι το
τότε το μέγιστό της είναι το 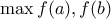 , το οποίο, αν και προφανές διαισθητικά, θέλει απόδειξη.
, το οποίο, αν και προφανές διαισθητικά, θέλει απόδειξη.
Αν η
 είναι κυρτή στο
είναι κυρτή στο ![\displaystyle{[a,b]} \displaystyle{[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/14f53999651f504e8f7c5c1b74530f3e.png) τότε το μέγιστό της είναι το
τότε το μέγιστό της είναι το 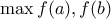 , το οποίο, αν και προφανές διαισθητικά, θέλει απόδειξη.
, το οποίο, αν και προφανές διαισθητικά, θέλει απόδειξη.- Παρ Μαρ 22, 2024 8:43 pm
- Δ. Συζήτηση: Διασκεδαστικά Μαθηματικά
- Θέμα: Μαθηματικές Διαδρομές_4_Σέξι Γωνία
- Απαντήσεις: 3
- Προβολές: 917
Re: Μαθηματικές Διαδρομές_4_Σέξι Γωνία
Μάλλον έχετε αντιληφθεί λάθος τι σημαίνει διασκεδαστικά μαθηματικά.
- Πέμ Μαρ 21, 2024 11:49 pm
- Δ. Συζήτηση: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
- Θέμα: Τρίγωνο σε έλλειψη
- Απαντήσεις: 6
- Προβολές: 2121
Re: Τρίγωνο σε έλλειψη
Χωρίς λογισμό: Ας είναι $\displaystyle{\frac{x^2}{A^2}+\frac{y^2}{B^2}=1}$ η έλλειψη και ας είναι $\displaystyle{K(A\sin a, B\cos a), L(A\sin b, B\cos b), M(A\sin c, B\cos c)}$ τρία σημεία αυτής. Από τη γνωστή σχέση $\displaystyle{(KLM)=\frac{1}{2} |\left|\displaystyle {\begin{array}{*{20}{c}} x_K&y...
- Τρί Μαρ 05, 2024 6:38 pm
- Δ. Συζήτηση: Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)
- Θέμα: ΑΡΧΙΜΗΔΗΣ 2024
- Απαντήσεις: 97
- Προβολές: 35754
Re: ΑΡΧΙΜΗΔΗΣ 2024
Έχοντας περάσει μία εβδομάδα γεμάτη refresh στο site στης Ελληνικής Μαθηματικής Εταιρίας, έχω να πω οτι τα χέρια μου κοντεύουν να βγάλουν φούσκες...Ας μην μας αφήνουν στην αγωνία αν δεν χρειάζεται και αν υπάρχει κάποιο πρόβλημα στην βαθμολόγηση θα ήταν καλό να λυθεί το συντομότερο δυνατόν.Πραγματικ...
- Πέμ Φεβ 22, 2024 6:33 pm
- Δ. Συζήτηση: Άλγεβρα - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Εξέταση σε εξίσωση βαθμού έξι
- Απαντήσεις: 4
- Προβολές: 1060
Re: Εξέταση σε εξίσωση βαθμού έξι
Με την παρατήρηση ότι  , η εξίσωση γράφεται
, η εξίσωση γράφεται
 και τα υπόλοιπα είναι απλά.
και τα υπόλοιπα είναι απλά.
 , η εξίσωση γράφεται
, η εξίσωση γράφεται και τα υπόλοιπα είναι απλά.
και τα υπόλοιπα είναι απλά.- Πέμ Φεβ 22, 2024 6:22 pm
- Δ. Συζήτηση: Προτεινόμενα Θέματα Μαθηματικών
- Θέμα: Ανισότητες από άλλες ανισότητες
- Απαντήσεις: 2
- Προβολές: 920
Re: Ανισότητες από άλλες ανισότητες
Αποδεικνύονται αμέσως και με απλή χρήση της ανισότητας ΑΜ-ΓΜ. Π.χ. για την πρώτη: $\displaystyle{a^4+3b^4>4|ab^3|\geq 4ab^3}$ $\displaystyle{b^4+3c^4>4|bc^3|\geq 4bc^3}$ $\displaystyle{c^4+3d^4>4|cd^3|\geq 4cd^3.}$ Με πρόσθεση λαμβάνουμε το ζητούμενο. Από την απόδειξη αυτή φαίνεται ότι η διάταξη δεν...
- Τετ Φεβ 14, 2024 11:30 am
- Δ. Συζήτηση: Ανάλυση
- Θέμα: Είναι το 0 σημείο καμπής;
- Απαντήσεις: 4
- Προβολές: 978
Re: Είναι το 0 σημείο καμπής;
Ωστόσο, στο  η
η  έχει κατακόρυφη εφαπτομένη, οπότε αυτή η περίπτωση δεν αφορά τους μαθητές. Υποθέτω για αυτόν τον λόγο το θέμα τοποθετήθηκε στο συγκεκριμένο φάκελο.
έχει κατακόρυφη εφαπτομένη, οπότε αυτή η περίπτωση δεν αφορά τους μαθητές. Υποθέτω για αυτόν τον λόγο το θέμα τοποθετήθηκε στο συγκεκριμένο φάκελο.
 η
η  έχει κατακόρυφη εφαπτομένη, οπότε αυτή η περίπτωση δεν αφορά τους μαθητές. Υποθέτω για αυτόν τον λόγο το θέμα τοποθετήθηκε στο συγκεκριμένο φάκελο.
έχει κατακόρυφη εφαπτομένη, οπότε αυτή η περίπτωση δεν αφορά τους μαθητές. Υποθέτω για αυτόν τον λόγο το θέμα τοποθετήθηκε στο συγκεκριμένο φάκελο.- Σάβ Φεβ 10, 2024 11:33 pm
- Δ. Συζήτηση: Γενικά Μηνύματα
- Θέμα: Ευχές
- Απαντήσεις: 7
- Προβολές: 1189
Re: Ευχές
Τι; ευχές μου στον Μπάμπη, με υγεία!
- Πέμ Φεβ 08, 2024 10:28 pm
- Δ. Συζήτηση: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
- Θέμα: Επιτέλους κάτι κοινό
- Απαντήσεις: 2
- Προβολές: 678
Re: Επιτέλους κάτι κοινό
Για $\displaystyle{a=3}$ θα θέλαμε να ισχύει $\displaystyle{3\sin x+\tan x\geq 4x}$ για κάθε $\displaystyle{x\in \left(0, \frac{\pi}{2}\right)}$, η οποία όμως αποτυγχάνει στο $\displaystyle{\frac{\pi}{4}}$. Για το δεύτερο ερώτημα: Κάθε τέτοιο $\displaystyle{a}$ θα ικανοποιεί την συνθήκη $\displaysty...
- Τετ Φεβ 07, 2024 10:02 pm
- Δ. Συζήτηση: Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)
- Θέμα: ΕΥΚΛΕΙΔΗΣ 2023 - 2024
- Απαντήσεις: 87
- Προβολές: 22174
Re: ΕΥΚΛΕΙΔΗΣ 2023 - 2024
Πάντως δεν μπορεί να αποφύγει κάνεις να παρατηρήσει την ισχυρή παρουσία των ιδιωτικών σχολείων... :!: Δείτε εδώ . Ισχύει αυτό που λέτε. Αλλά σίγουρα δεν έχει απαραίτητα σχέση με διαφορά ποιότητας μαθήματος. Εννοείται! Οι λόγοι πρέπει να αναζητηθούν αλλού. Λ.χ. στο γεγονός ότι είναι πάγια τακτική με...
- Δευ Φεβ 05, 2024 3:14 pm
- Δ. Συζήτηση: Άλγεβρα - Επίπεδο Αρχιμήδη (Seniors)
- Θέμα: Ανισότητα
- Απαντήσεις: 1
- Προβολές: 1795
Re: Ανισότητα
Με χρήση της $\displaystyle{h_a=\frac{2E}{a}}$, όπου $\displaystyle{E}$ το εμβαδόν, η ζητούμενη γράφεται $\displaystyle{\sum \frac{1}{c}\sqrt{\frac{a^2+b^2}{2ab}}\leq \frac{\sqrt{3}R}{4r^2}.}$ Λόγω της ανισότητας του Τσίντσιφα (βλ. American Mathematical Monthly, Problem E2471) $\displaystyle{\boxed{...
- Παρ Φεβ 02, 2024 9:51 pm
- Δ. Συζήτηση: Άλγεβρα - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Υπολογισμός γινομένου
- Απαντήσεις: 1
- Προβολές: 718
Re: Υπολογισμός γινομένου
Υποθέτω ότι επειδή είναι στον φάκελο Θαλή/Ευκλείδη υπάρχει κάτι απλούστερο, αλλά γράφω τη λύση που σκέφτηκα με το που είδα το πρόβλημα. Το ζητούμενο είναι το $\displaystyle{M=\prod_{k=0}^{14}\sin a_k}$, όπου $\displaystyle{a_k=\frac{(6k+1)\pi}{45}}$. Ας είναι $\displaystyle{x_k=\cos a_k+i\sin a_k,}$...
- Κυρ Ιαν 14, 2024 12:21 pm
- Δ. Συζήτηση: Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)
- Θέμα: Πολυώνυμα!
- Απαντήσεις: 2
- Προβολές: 701
Re: Πολυώνυμα!
Η σχέση γράφεται ως
 ,
,
οπότε για το πολυώνυμο ισχύει
ισχύει  Τότε ως γνωστόν είναι
Τότε ως γνωστόν είναι 
 ,
,οπότε για το πολυώνυμο
 ισχύει
ισχύει  Τότε ως γνωστόν είναι
Τότε ως γνωστόν είναι 
- Παρ Ιαν 05, 2024 11:36 pm
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Β'
- Θέμα: Η στιγμή του συνημιτόνου
- Απαντήσεις: 3
- Προβολές: 882
Re: Η στιγμή του συνημιτόνου
Από τον νόμο των συνημιτόνων στα τρίγωνα $\displaystyle{ABD,BCD}$ έχουμε αντίστοιχα $\displaystyle{BD^2=4^2+5^2-2\cdot 4\cdot 5\cos A}$ και $\displaystyle{BD^2=6^2+5^2-2\cdot 5\cdot 6\cos C.}$ Από αυτές και επειδή $\displaystyle{\cos A=-\cos C}$ βρίσκουμε $\displaystyle{\cos C=\frac{1}{5}.}$ Όμως $\...
- Σάβ Δεκ 23, 2023 12:49 am
- Δ. Συζήτηση: Γενικά
- Θέμα: Ρητή προσέγγιση του ln2
- Απαντήσεις: 6
- Προβολές: 3230
Ρητή προσέγγιση του ln2
Είναι  και
και  .
.
Πώς θα αποδείξουμε ότι ;
;
 και
και  .
.Πώς θα αποδείξουμε ότι
 ;
;