 είναι μέσο του
είναι μέσο του  . Βρείτε τη γωνία
. Βρείτε τη γωνία 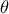 .
.24 ώρες για τους μαθητές .
Συντονιστές: silouan, Doloros, george visvikis
 είναι μέσο του
είναι μέσο του  . Βρείτε τη γωνία
. Βρείτε τη γωνία 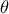 .
.Καλησπέρα.
 ο περιγεγραμμένος κύκλος του τριγώνου
ο περιγεγραμμένος κύκλος του τριγώνου  και ας είναι
και ας είναι  το κέντρο του .
το κέντρο του .  είναι ισόπλευρο. Επίσης θα είναι
είναι ισόπλευρο. Επίσης θα είναι  και επειδή
και επειδή  έπεται ότι
έπεται ότι  . Τέλος παρατηρούμε ότι τα τρίγωνα
. Τέλος παρατηρούμε ότι τα τρίγωνα  και
και  είναι ίσα . Οπότε
είναι ίσα . Οπότε  .
.α) Τρόπος
 στο
στο  .
.

 και ακτίνα
και ακτίνα 
 από το
από το  .
.




george visvikis έγραψε: ↑Πέμ Ιουν 18, 2020 2:36 pmΈστωη προβολή του
στην
και
το μέσο του
άρα
και κατά συνέπεια

 που τέμνει στο
που τέμνει στο  την ευθεία
την ευθεία  .
.  οι προβολές του
οι προβολές του  στις ευθείες :
στις ευθείες :  .
. γιατί οι
γιατί οι  είναι διχοτόμοι των γωνιών :
είναι διχοτόμοι των γωνιών :  .
. είναι τετράγωνο και έτσι :
είναι τετράγωνο και έτσι : 
 . Τότε
. Τότε  και
και  .
. διχοτόμος της
διχοτόμος της  άρα
άρα  και
και  (1)
(1) είναι ίσα (π-γ-π) συνεπώς
είναι ίσα (π-γ-π) συνεπώς 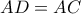 και επειδή
και επειδή  έχουμε
έχουμε  . (2)
. (2)  εγγράψιμο. Συνεπώς
εγγράψιμο. Συνεπώς 
 συμμετρικό του
συμμετρικό του  ως προς
ως προς  και
και  συμμετρικό του
συμμετρικό του  ως προς
ως προς  θα έχουμε ότι
θα έχουμε ότι και
και  ισόπλευρο με
ισόπλευρο με 
 (σχέση επίκεντρης-εγγεγραμένης)
(σχέση επίκεντρης-εγγεγραμένης)Εστω ότι
 Τότε
Τότε 
 είναι εγγράψιμο και
είναι εγγράψιμο και  Το τρίγωνο
Το τρίγωνο  είναι ισόπλευρο και η
είναι ισόπλευρο και η  μεσοκάθετος άρα
μεσοκάθετος άρα
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης