Καθετότητα σε ορθογώνιο τρίγωνο

#1

: Καθετότητα σε ορθογώνιο τρίγωνο..png (15.57 KiB) Προβλήθηκε 1044 φορές

Στην υποτείνουσα

ορθογωνίου τριγώνου ABC

θεωρούμε σημείο

και έστω

το μέσο του MC.

Η παράλληλη από το

στην

τέμνει την

στο

και ο κύκλος που διέρχεται από τα B, D, C

την

στο

Να δείξετε ότι $BE\bot AN.$

#2

Αν

το σημείο τομής των $CA\,\,\kappa \alpha \iota \,\,MD$ από το $\vartriangle MSC$ θα είναι το

μέσο του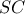

και το τρίγωνο BSC

ισοσκελές με κορυφή το

.

Διαδοχικά έχω :

$\widehat {{a_4}} = \widehat {{a_3}}\,\,\,\kappa \alpha \iota \,\,\widehat {{a_3}} = \widehat {{a_2}}$ ( εξωτερική του εγγεγραμμένου τετραπλεύρου DBCE

) .

: κάθετη σε ορθογώνιο τρίγωνο_oritzin_1.png (23.49 KiB) Προβλήθηκε 1015 φορές

Άρα αν η

τμήσει την

στο

το τετράπλευρο STDA

είναι εγγράψιμο.

Το

είναι ορθόκεντρο του $\vartriangle SBE$ , συνεπώς : $\left\{ \begin{gathered} BE \bot SM \hfill \\ SM//AN \hfill \\ \end{gathered} \right. \Rightarrow BE \bot AN$

Μιχάλης Τσουρακάκης · #3

george visvikis έγραψε: ↑
Κυρ Ιουν 28, 2020 7:10 pm
Καθετότητα σε ορθογώνιο τρίγωνο..png
Στην υποτείνουσα ορθογωνίου τριγώνου θεωρούμε σημείο και έστω το μέσο του

Η παράλληλη από το στην τέμνει την στο και ο κύκλος που διέρχεται από τα την

στο Να δείξετε ότι $BE\bot AN.$

$DM//AN \Rightarrow DK=KC$ ,συνεπώς οι κόκκινες γωνίες είναι ίσες άρα $BE \bot AN$

: Καθετότητα σε ορθογώνιο τρίγωνο.png (12.87 KiB) Προβλήθηκε 986 φορές

p_gianno · #4

: καθετότητα.png (62.59 KiB) Προβλήθηκε 951 φορές

$CZ //AN \;\;\; (N \in BA)$ συνεπώς DA=AZ

και επειδή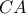

διάμεσος και ύψος του τριγώνου DCZ

συμπεραίνουμε ότι

$CD=CZ\;$ ή $\;\widehat{ADC}=\widehat{Z}$ (1)

$\widehat{BDC}=\widehat{BEC} \rightarrow \widehat{ADC}=\widehat{AEB}$ (2)

Από 1 και 2 έχω $\widehat{AEB} = \widehat{Z}$ δηλαδή ZAEK

εγγράψιμο συνεπώς K=90^0

.

Δηλαδή $BK \perp ZC \rightarrow BE \perp AN$

Καθετότητα σε ορθογώνιο τρίγωνο

Καθετότητα σε ορθογώνιο τρίγωνο

Re: Καθετότητα σε ορθογώνιο τρίγωνο

Re: Καθετότητα σε ορθογώνιο τρίγωνο

Re: Καθετότητα σε ορθογώνιο τρίγωνο

Μέλη σε σύνδεση