 , θεωρούμε χορδή
, θεωρούμε χορδή  με απόστημα
με απόστημα  και μέσο
και μέσο  . Γράφουμε το εντός του κύκλου
. Γράφουμε το εντός του κύκλουημικύκλιο διαμέτρου
 . Σημείο
. Σημείο  κινείται στο μεγάλο τόξο
κινείται στο μεγάλο τόξο  του κύκλου , ώστε οι
του κύκλου , ώστε οι 
να τέμνουν το ημικύκλιο στα σημεία
 αντίστοιχα . Αν η διχοτόμος της
αντίστοιχα . Αν η διχοτόμος της  , τέμνει το ύψος
, τέμνει το ύψος 
στο σημείο
 , δείξτε ότι το άθροισμα
, δείξτε ότι το άθροισμα  παραμένει σταθερό .
παραμένει σταθερό .
 το σημείο τομής των
το σημείο τομής των 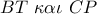 που προφανώς είναι το ορθόκεντρο του
που προφανώς είναι το ορθόκεντρο του  .
.  είναι ο κύκλος του
είναι ο κύκλος του  και περνά από το μέσο
και περνά από το μέσο 
 αυτό είναι διχοτόμος της
αυτό είναι διχοτόμος της  .
. είναι παραλληλόγραμμο και έτσι
είναι παραλληλόγραμμο και έτσι  σταθερό
σταθερό ύψη του τριγώνου
ύψη του τριγώνου  και
και
 (στο μέτρο)
(στο μέτρο) εγγράψιμμο
εγγράψιμμο  συνεπώς
συνεπώς διάμετρος του περιγγεγραμμένου κύκλου
διάμετρος του περιγγεγραμμένου κύκλου  . Το κέντρο του
. Το κέντρο του  αλλά και στην διάμετρό του. Συνεπώς
αλλά και στην διάμετρό του. Συνεπώς 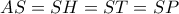 .
.  και έχει σταθερή ακτίνα επειδή
και έχει σταθερή ακτίνα επειδή και
και  (1)
(1) παραμένει σταθερό ως πρός το μέγεθός του αφού και οι πλευρές και οι γωνίες του είναι σταθερές ως προς το μέτρο τους για τις διάφορες θέσεις του
παραμένει σταθερό ως πρός το μέγεθός του αφού και οι πλευρές και οι γωνίες του είναι σταθερές ως προς το μέτρο τους για τις διάφορες θέσεις του  (2)
(2)