Τραπεζιακοί λογαριασμοί 3

KARKAR · #1

: Τραπεζιακοί λογαριασμοί.png (10.64 KiB) Προβλήθηκε 947 φορές

Στο ισοσκελές τραπέζιο ABCD

, τα σημεία M , K , N

, είναι τα μέσα των AD , CD , BC

αντίστοιχα και είναι γνωστό ότι : AD=3 , MN=5 , BC=7

. Ο κύκλος διαμέτρου

τέμνει το

στα σημεία S , T

. Υπολογίστε το

και δείξτε ότι : $DS \perp CS , KS \perp AB$ .

#2

KARKAR έγραψε: ↑
Τετ Απρ 15, 2020 8:37 pm
Τραπεζιακοί λογαριασμοί.pngΣτο ισοσκελές τραπέζιο , τα σημεία , είναι τα μέσα των

αντίστοιχα και είναι γνωστό ότι : . Ο κύκλος διαμέτρου

τέμνει το στα σημεία . Υπολογίστε το και δείξτε ότι : $DS \perp CS , KS \perp AB$ .

: Τραπεζιακοί λογαριασμοί.3.png (16.67 KiB) Προβλήθηκε 880 φορές

Φέρνω το ύψος

του τραπεζίου και εύκολα BE=2.

Με Πυθαγόρειο βρίσκω $\displaystyle AB = CD = \sqrt {29}$

και με θεώρημα Πτολεμαίου στο ισοσκελές τραπέζιο, $\displaystyle 3 \cdot 7 + 29 = B{D^2} \Leftrightarrow BD = AC = 5\sqrt 2 .$

Με ν. συνημιτόνου στο ADB,

είναι $\displaystyle A\widehat DB = 45^\circ = D\widehat BC = B\widehat ST,$ άρα το ETSB

είναι ισοσκελές

τραπέζιο και $\boxed{ST=BE=2}$ Είναι ακόμα $AC\bot BD$ και επειδή $A\widehat SB=90^\circ$ το

είναι σημείο τομής

των διαγωνίων και $\boxed{DS\bot CS}$ Όσο για το $KS\bot AB$ είναι θεώρημα (Σε εγγράψιμο τετράπλευρο με κάθετες

διαγωνίους, η ευθεία που διέρχεται από το σημείο τομής των διαγωνίων και το μέσο μιας πλευράς είναι κάθετη

στην απέναντι πλευρά). Πράγματι, οι ίσες μπλε γωνίες στο σχήμα, αποδεικνύουν το ζητούμενο.

p_gianno · #3

KARKAR έγραψε: ↑
Τετ Απρ 15, 2020 8:37 pm
Τραπεζιακοί λογαριασμοί.pngΣτο ισοσκελές τραπέζιο , τα σημεία , είναι τα μέσα των

αντίστοιχα και είναι γνωστό ότι : . Ο κύκλος διαμέτρου

τέμνει το στα σημεία . Υπολογίστε το και δείξτε ότι : $DS \perp CS , KS \perp AB$ .

: trapeziaka.png (49.15 KiB) Προβλήθηκε 855 φορές

Έστω

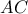διαγώνιος και

ύψος του τραπεζίου. Τότε EN=AM=3/2

και

Με ΠΘ στο ορθογώνιο $\triangle AEC$ παίρνουμε BE=2

και $AB= \sqrt{29}$

Επίσης EC=EN+NC=3/2+7/2=10/2=5=MN=AE

Συνεπώς $\triangle AEC$ ορθ. ισοσκελές και επομένως $\hat{ACE}=45^0$

Αν

το κέντρο του κύκλου διαμέτρου

τότε

συνεπώς $\hat{BNH}=\hat{ACE}=45^0$ άρα

διχοτόμος της $\hat{BNM}=90^0$ . Είναι τώρα η

άξονας συμμετρίας του σχήματος “κύκλος-γωνία

BNM

”. Άμεσα έχουμε ST=BE=2

B) Η μεσοκάθετος των βάσεων του ισοσκελούς τραπεζίου είναι άξονας συμμετρίας του. Προφανώς το συμμετρικό του ημικυκλίου BSA

είναι

το ημικύκλιο DSC

στο οποίο είναι εγγεγραμμένη η γωνία DSC

που βαίνει στην διάμετρο

. Άρα

ή $DS \perp SC$

Γ) Θα δείξουμε ότι το σημείο τομής των διαγωνίων συμπίπτει με το

Πράγματι

και

. Από αυτές προκύπτει ότι $AC \perp BD$ συνεπώς δεν μπορεί

παρά η δοθείσα γωνία DSC

να ταυτίζεται με την ορθή των διαγωνίων άρα C,S,A

και

συνευθειακά.

$\hat{ATS}=180^0- \hat{TAS} - \hat{AST}=180^0 - \hat{SDC} - \hat{KSC} =180^0 - \hat{SDC} - \hat{DCS}=\hat{DSC} = 90^0$

(

διάμεσος ορθογωνίου τριγώνου άρα SKC

ισοσκελές άρα ίσες γωνίες βάσης))

Τραπεζιακοί λογαριασμοί 3

Τραπεζιακοί λογαριασμοί 3

Re: Τραπεζιακοί λογαριασμοί 3

Re: Τραπεζιακοί λογαριασμοί 3

Μέλη σε σύνδεση