 , ημικυκλίου διαμέτρου
, ημικυκλίου διαμέτρου  , φέρνω εφαπτομένη και συναντά την κάθετη στο
, φέρνω εφαπτομένη και συναντά την κάθετη στο  επί την
επί την  στο
στο  .
.Ας είναι
 η προβολή του
η προβολή του  στην
στην  . Φέρνω και την κάθετη από το
. Φέρνω και την κάθετη από το  στην
στην  και τέμνει την
και τέμνει την  στο
στο  .
.Δείξτε ότι το
 είναι μέσο του
είναι μέσο του 
Δεκτή κάθε λύση.
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , ημικυκλίου διαμέτρου
, ημικυκλίου διαμέτρου  , φέρνω εφαπτομένη και συναντά την κάθετη στο
, φέρνω εφαπτομένη και συναντά την κάθετη στο  επί την
επί την  στο
στο  .
. η προβολή του
η προβολή του  στην
στην  . Φέρνω και την κάθετη από το
. Φέρνω και την κάθετη από το  στην
στην  και τέμνει την
και τέμνει την  στο
στο  .
. είναι μέσο του
είναι μέσο του 
 η προβολή του
η προβολή του  στην
στην  και
και  το σημείο τομής των
το σημείο τομής των  Προφανώς
Προφανώς  είναι το ορθόκεντρο του
είναι το ορθόκεντρο του  Αν
Αν  είναι το μέσο του
είναι το μέσο του 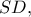 τότε και το
τότε και το  θα είναι μέσο του
θα είναι μέσο του  Σύμφωνα λοιπόν με αυτήν (#4)
Σύμφωνα λοιπόν με αυτήν (#4) 





 και από τα όμοια τρίγωνα
και από τα όμοια τρίγωνα 

 που αποδεικνύει το ζητούμενο.
που αποδεικνύει το ζητούμενο.Η
 είναι συμμετροδιάμεσος στο
είναι συμμετροδιάμεσος στο 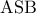 άρα αν
άρα αν  η εφαπτομένη του ημικυκλίου στο
η εφαπτομένη του ημικυκλίου στο  θα είναι
θα είναι  .Έστω
.Έστω  η παράλληλη από το
η παράλληλη από το  στην
στην  .
. οπότε από γνωστή πρόταση
οπότε από γνωστή πρόταση  και αφού
και αφού  το ζητούμενο έπεται.
το ζητούμενο έπεται.Αν
 το μέσο της
το μέσο της  τότε θα είναι:
τότε θα είναι:  .
.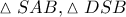 τα τμήματα
τα τμήματα 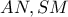 είναι ομόλογα και με
είναι ομόλογα και με  διάμεσο του
διάμεσο του  διάμεσος του
διάμεσος του  και το ζητούμενο έχει αποδειχτεί.
και το ζητούμενο έχει αποδειχτεί. (1)
(1) (εντός εναλλάξ) (2)
(εντός εναλλάξ) (2) διχοτόμος της
διχοτόμος της  .
. εξωτερική διχοτόμος της
εξωτερική διχοτόμος της  συνεπώς η δέσμη
συνεπώς η δέσμη  είναι αρμονική
είναι αρμονική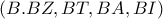 είναι αρμονική και επειδή
είναι αρμονική και επειδή  έχουμε
έχουμε 
 και θεώρημα χορδής – εφαπτομένης έχουμε για τις γωνίες
και θεώρημα χορδής – εφαπτομένης έχουμε για τις γωνίες  συνεπώς
συνεπώς  εκ του μέσου
εκ του μέσου  της
της  άρα
άρα  μέσον της
μέσον της 


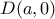 και όλα τα άλλα σημεία εκφράζονται με τη βοήθεια της μεταβλητής
και όλα τα άλλα σημεία εκφράζονται με τη βοήθεια της μεταβλητής  .
. η τομή των
η τομή των  , τότε τα ορθογώνια τρίγωνα
, τότε τα ορθογώνια τρίγωνα  είναι όμοια με κάθετες τις υποτείνουσες τους. Αν
είναι όμοια με κάθετες τις υποτείνουσες τους. Αν  το μέσον του
το μέσον του  και επειδή
και επειδή  είναι το μέσο του ομόλογου του
είναι το μέσο του ομόλογου του  , τότε (από την καθετότητα των υποτεινουσών που αναφέραμε),
, τότε (από την καθετότητα των υποτεινουσών που αναφέραμε),  Λόγω του μονοσήμαντου της καθέτου από σημείο σε ευθεία, η απόδειξη είναι ήδη ολοκληρωμένη.
Λόγω του μονοσήμαντου της καθέτου από σημείο σε ευθεία, η απόδειξη είναι ήδη ολοκληρωμένη. είναι το ορθόκεντρο του
είναι το ορθόκεντρο του  άρα
άρα  , αφού
, αφού  .Αρκεί το
.Αρκεί το  να είναι το μέσον του
να είναι το μέσον του 
 τέμνονται στο
τέμνονται στο  . Όπως και ΕΔΩ τα
. Όπως και ΕΔΩ τα  είναι συζυγή αρμονικά των
είναι συζυγή αρμονικά των  . Με
. Με  παίρνουμε
παίρνουμε 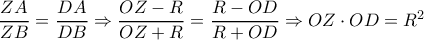
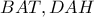 δίνει
δίνει  και των
και των  δίνει
δίνει  .
. αρκεί λοιπόν να δείξουμε την
αρκεί λοιπόν να δείξουμε την  .
.  έχουμε
έχουμε  που ισχύει!
που ισχύει! είναι το μέσον του
είναι το μέσον του  και
και  το μέσον του
το μέσον του  . Φιλικά, Γιώργος.
. Φιλικά, Γιώργος.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες