 κινείται στην προέκταση της διαμέτρου
κινείται στην προέκταση της διαμέτρου  , ενός ημικυκλίου . Φέρουμε το εφαπτόμενο τμήμα
, ενός ημικυκλίου . Φέρουμε το εφαπτόμενο τμήμα  και
και την τέμνουσα - διχοτόμο
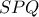 . Αν
. Αν  , υπολογίστε το άθροισμα :
, υπολογίστε το άθροισμα :  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 κινείται στην προέκταση της διαμέτρου
κινείται στην προέκταση της διαμέτρου  , ενός ημικυκλίου . Φέρουμε το εφαπτόμενο τμήμα
, ενός ημικυκλίου . Φέρουμε το εφαπτόμενο τμήμα  και
και 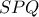 . Αν
. Αν  , υπολογίστε το άθροισμα :
, υπολογίστε το άθροισμα :  .
.Έστω
 το κέντρο και το μέσο του ημικυκλίου,
το κέντρο και το μέσο του ημικυκλίου,  η ακτίνα του,
η ακτίνα του,  το σημείο τομής των των
το σημείο τομής των των  και
και  το
το  Έστω ακόμα
Έστω ακόμα  οι προβολές των
οι προβολές των  στην
στην  και
και  το σημείο τομής της
το σημείο τομής της  με την
με την  Οι μπλε γωνίες είναι ίσες γιατί είναι συμπληρωματικές των πράσινων, οπότε
Οι μπλε γωνίες είναι ίσες γιατί είναι συμπληρωματικές των πράσινων, οπότε  και
και 
 το
το  είναι μέσο του
είναι μέσο του  άρα και
άρα και  μέσο του
μέσο του 


 είναι μέσο του ημικυκλίου .
είναι μέσο του ημικυκλίου . το
το 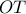 είναι ύψος και η
είναι ύψος και η  διχοτόμος οπότε το
διχοτόμος οπότε το 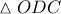 είναι ισοσκελές
είναι ισοσκελές  να είναι ισοσκελές τραπέζιο.
να είναι ισοσκελές τραπέζιο. κάθετη στην
κάθετη στην  και τέμνει τη διάμετρο
και τέμνει τη διάμετρο  στο
στο  .
. είναι παραλληλόγραμμο και
είναι παραλληλόγραμμο και  θα είναι και το
θα είναι και το 
 και άρα
και άρα  .
.Καλησπέρα το τρίγωνο
 είναι ισοσκελές γιατί
είναι ισοσκελές γιατί  . Αν
. Αν 
 είναι ισοσκελές με
είναι ισοσκελές με  Αρα το σημείο
Αρα το σημείο  είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  ,
,
 το σημείο
το σημείο 
 Στο τραπέζιο
Στο τραπέζιο  ,η
,η  είναι διαμεσος και
είναι διαμεσος και
Έστω
 το μέσο της χορδής
το μέσο της χορδής  . Είναι
. Είναι  το κέντρο του κύκλου και
το κέντρο του κύκλου και  απόστημα της χορδής
απόστημα της χορδής  συνεπώς
συνεπώς  .
. κατά την θετική φορά γύρω από το
κατά την θετική φορά γύρω από το  κατά
κατά 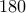 μοίρες. Είναι τότε
μοίρες. Είναι τότε  . Επειδή
. Επειδή 
 έπεται ότι
έπεται ότι  συμμετρικό του
συμμετρικό του  και ως προς την ευθεία
και ως προς την ευθεία  συνεπώς
συνεπώς  ανήκει ευθεία
ανήκει ευθεία  .
. (1) και
(1) και  (2) (από την αξονική συμμετρία ως προς
(2) (από την αξονική συμμετρία ως προς  )
) και επειδή
και επειδή  εφαπτομένη του κύκλου από το σημείο
εφαπτομένη του κύκλου από το σημείο  έπεται ότι και
έπεται ότι και  εφαπτομένη
εφαπτομένη το νέο σημείο επαφής τότε
το νέο σημείο επαφής τότε  .
. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες