Γινόμενο πολλαπλάσιο αθροίσματος

KARKAR · #1

: Γινόμενο πολλαπλάσιο αθροίσματος.png (4.6 KiB) Προβλήθηκε 130 φορές

Ευθεία διερχόμενη από το σημείο S(8,4)

, τέμνει τον ημιάξονα

στο σημείο

και την ημιευθεία

$y=\dfrac{4}{3}x$ , του πρώτου τεταρτημορίου στο σημείο

. Υπολογίστε τον λόγο : $\dfrac{OA\cdot OB}{OA+OB}$ .

#2

Είναι ίδια με την πρόσφατη άσκηση εδώ (βλέπε ποστ #3) μόνο που το σχήμα έχει περιστραφεί. Ο ρόμβος του εκεί σχήματος είναι ο με κορυφές (0,0), (0,5), (8,4),(3,4)

ρόμβος στο εδώ.

Nikitas K. · #3

Θέτοντας

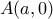και

διότι ανήκει στην ευθεία $y = \dfrac{4}{3}x$

$AS:\qquad y = \dfrac{4}{8-a}(x-a)$ μόνο αν $a\neq 8$

Επειδη το σημείο

ανήκει στην ευθεία

οι συντεταγμένες του επαληθεύονται οπότε:

$4b = \dfrac{4}{8-a}(3b-a) \Leftrightarrow a = \dfrac{5b}{b-1}$ μόνο αν $b\neq 1$

Έχουμε:
$OA = a = \dfrac{5b}{b-1}$ και OB = 5b

(έστω

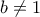
και

μη αρνητικά)

$OA \cdot OB = \dfrac{25b^2}{b-1}$ ενώ $OA+OB = \dfrac{5b^2}{b-1}$

Επομένως ο ζητούμενος λόγος είναι

Τώρα αν

τότε η ευθεία που διέρχεται από το σημείο

και τέμνει την

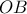θα είναι παράλληλη στον άξονα των τετμημένων που είναι άτοπο.

Επίσης αν a = 8

τότε $AS: \qquad x = 8$ άρα $B(8, \dfrac{32}{3})$ επομένως OA = 8

και $OB = \dfrac{40}{3}$ οπότε και πάλι ο ζητούμενος λόγος είναι ίσος με

Κατά την επεξεργασία προστέθηκε και η περίπτωση όπου a = 8

#4

KARKAR έγραψε: ↑
Παρ Σεπ 19, 2025 8:58 am
Γινόμενο πολλαπλάσιο αθροίσματος.pngΕυθεία διερχόμενη από το σημείο , τέμνει τον ημιάξονα στο σημείο και την ημιευθεία

$y=\dfrac{4}{3}x$ , του πρώτου τεταρτημορίου στο σημείο . Υπολογίστε τον λόγο : $\dfrac{OA\cdot OB}{OA+OB}$ .

Έστω

Είναι, $\displaystyle \tan (\theta + \varphi ) = \frac{4}{3} \Leftrightarrow \frac{{\frac{1}{2} + \tan \varphi }}{{1 - \frac{1}{2}\tan \varphi }} = \frac{4}{3} \Leftrightarrow \tan \theta = \tan \varphi = \frac{1}{2}.$

Είναι ακόμα $\displaystyle OS = 4\sqrt 5,$ $\displaystyle \cos \theta = \frac{2}{{\sqrt 5 }}$ και με νόμο συνημιτόνων παίρνω:

: Γ.ΠΑ.png (12.09 KiB) Προβλήθηκε 87 φορές

$\displaystyle \left\{ \begin{gathered} S{A^2} = {a^2} + 80 - 16a \hfill \\ S{B^2} = {b^2} + 80 - 16b \hfill \\ \end{gathered} \right.$ . Αλλά από θεώρημα διχοτόμου είναι:

$\displaystyle \frac{{S{A^2}}}{{S{B^2}}} = \frac{{{a^2}}}{{{b^2}}} \Leftrightarrow$ $\boxed{5(b-a)(a+b)=ab(b-a)}$

$\displaystyle \bullet$ Αν $a\ne b,$ τότε $\boxed{\frac{ab}{a+b}=5}$

$\displaystyle \bullet$ Αν a= b,

τότε

οπότε και πάλι ισχύει η παραπάνω τιμή.

Γινόμενο πολλαπλάσιο αθροίσματος

Γινόμενο πολλαπλάσιο αθροίσματος

Re: Γινόμενο πολλαπλάσιο αθροίσματος

Re: Γινόμενο πολλαπλάσιο αθροίσματος

Re: Γινόμενο πολλαπλάσιο αθροίσματος

Μέλη σε σύνδεση