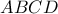 ισχύει
ισχύει  . Οι κύκλοι
. Οι κύκλοι  τέμνονται για δεύτερη φορά στο
τέμνονται για δεύτερη φορά στο  . Η ευθεία
. Η ευθεία  τέμνει την
τέμνει την  στο
στο  και ο περιγεγραμμένος κύκλος του
και ο περιγεγραμμένος κύκλος του  τέμνει την
τέμνει την 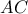 στο
στο  . Να αποδειχθεί ότι το
. Να αποδειχθεί ότι το  είναι το έγκεντρο του
είναι το έγκεντρο του  .
.Συντονιστές: vittasko, silouan, rek2
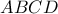 ισχύει
ισχύει  . Οι κύκλοι
. Οι κύκλοι  τέμνονται για δεύτερη φορά στο
τέμνονται για δεύτερη φορά στο  . Η ευθεία
. Η ευθεία  τέμνει την
τέμνει την  στο
στο  και ο περιγεγραμμένος κύκλος του
και ο περιγεγραμμένος κύκλος του  τέμνει την
τέμνει την 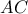 στο
στο  . Να αποδειχθεί ότι το
. Να αποδειχθεί ότι το  είναι το έγκεντρο του
είναι το έγκεντρο του  .
.Υποθέτω ότι η η ισότητα της εκφώνησης δεν χρειάζεται. Αν κάνω λάθος η παρακάτω λύση είναι άκυρη.
 των κύκλων
των κύκλων  είναι μεσοκάθετος της κοινής χορδής
είναι μεσοκάθετος της κοινής χορδής  άρα
άρα  από
από  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  Θα δείξω ότι και η
Θα δείξω ότι και η  είναι διχοτόμος της
είναι διχοτόμος της  Έστω
Έστω  το κέντρο του κύκλου
το κέντρο του κύκλου  Τα σημεία
Τα σημεία  είναι συνευθειακά, αφού και οι τρεις κύκλοι έχουν κοινή χορδή.
είναι συνευθειακά, αφού και οι τρεις κύκλοι έχουν κοινή χορδή. το σημείο τομής αυτού του κύκλου με την
το σημείο τομής αυτού του κύκλου με την  Είναι,
Είναι, 
 οπότε η
οπότε η  είναι διχοτόμος της
είναι διχοτόμος της  και το ζητούμενο αποδείχτηκε.
και το ζητούμενο αποδείχτηκε.Έχετε δίκιο, δεν το παρατήρησα.george visvikis έγραψε: ↑Πέμ Φεβ 20, 2025 9:41 amΥποθέτω ότι η η ισότητα της εκφώνησης πρέπει να είναιΑν κάνω λάθος η παρακάτω λύση είναι άκυρη.
Τελικά, νομίζω ότι ισχύει σε κάθε παραλληλόγραμμο. Η ισότητα δεν χρειάζεται.∫ot.T. έγραψε: ↑Πέμ Φεβ 20, 2025 9:52 amΈχετε δίκιο, δεν το παρατήρησα.george visvikis έγραψε: ↑Πέμ Φεβ 20, 2025 9:41 amΥποθέτω ότι η η ισότητα της εκφώνησης πρέπει να είναιΑν κάνω λάθος η παρακάτω λύση είναι άκυρη.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες