 , για τον καθέ από τους οποίους υπάρχει συνάρτηση
, για τον καθέ από τους οποίους υπάρχει συνάρτηση  τέτοια, ώστε
τέτοια, ώστε 
για οποιοδήποτε
 .
.Συντονιστές: achilleas, emouroukos, silouan
 , για τον καθέ από τους οποίους υπάρχει συνάρτηση
, για τον καθέ από τους οποίους υπάρχει συνάρτηση  τέτοια, ώστε
τέτοια, ώστε 
 .
.![a\in[0,1] a\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e09d0e6b79da6db2cc3e8cea1738a1e6.png) η
η  δεν υπάρχει
δεν υπάρχει η
η  υπάρχει
υπάρχει θα πρέπει:
θα πρέπει:





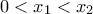 ώστε
ώστε 


 άτοπο
άτοπο





 ,
,  τότε
τότε  για κάποιο
για κάποιο 

 οπότε
οπότε  και αυτό αποδεικνύει τον εγκλεισμό.
και αυτό αποδεικνύει τον εγκλεισμό. τότε
τότε  ενώ
ενώ  και αυτό αποδεικνύει τον εγκλεισμό.
και αυτό αποδεικνύει τον εγκλεισμό. με
με  κατ' αρχάς θα πρέπει
κατ' αρχάς θα πρέπει  . Επίσης
. Επίσης  οπότε θα υπάρχει
οπότε θα υπάρχει  ώστε
ώστε  οπότε από το #3. θα έχουμε
οπότε από το #3. θα έχουμε  και συνεπως
και συνεπως  άτοπο.
άτοπο. με
με  θα πρέπει κατ' αρχάς
θα πρέπει κατ' αρχάς  . Θεωρούμε
. Θεωρούμε  . Επειδή η
. Επειδή η  είναι 1-1 θα πρέπει
είναι 1-1 θα πρέπει  οπότε θα υπάρχει
οπότε θα υπάρχει  ώστε
ώστε  οπότε
οπότε  και
και  άτοπο.
άτοπο. . Θα πρέπει
. Θα πρέπει  οπότε θα υπάρχει
οπότε θα υπάρχει  ώστε
ώστε  άτοπο αφού η
άτοπο αφού η  είναι 1-1.
είναι 1-1.

 που θα ικανοποιεί τη δοσμένη συναρτησιακή εξίσωση. Πρώτα όμως θα τροποιήσουμε την εξίσωση ώστε να καταστεί πιο διαχειρίσιμη.
που θα ικανοποιεί τη δοσμένη συναρτησιακή εξίσωση. Πρώτα όμως θα τροποιήσουμε την εξίσωση ώστε να καταστεί πιο διαχειρίσιμη. είναι αντιστρέψιμη.
είναι αντιστρέψιμη.  για κάθε
για κάθε 
 για κάθε
για κάθε 
 για κάθε
για κάθε  με
με 

 και
και 
 με
με 
 είναι, συνεχής, επί, 1-1, γνησίως αύξουσα και
είναι, συνεχής, επί, 1-1, γνησίως αύξουσα και  για κάθε
για κάθε 
 ώστε για κάθε
ώστε για κάθε  να ισχύει η συνεπαγωγή
να ισχύει η συνεπαγωγή
 και
και 
 θα είναι η ζητούμενη συνάρτηση
θα είναι η ζητούμενη συνάρτηση 

 η οποία είναι γνησίως αύξουσα, συνεχής, επί και
η οποία είναι γνησίως αύξουσα, συνεχής, επί και  για κάθε
για κάθε 

 και η
και η  είναι γνησίως αύξουσα (αποδεικνύεται επαγωγικά) και επειδή η
είναι γνησίως αύξουσα (αποδεικνύεται επαγωγικά) και επειδή η  δεν έχει σταθερά σημεία θα πρέπει
δεν έχει σταθερά σημεία θα πρέπει 
 με τη βοήθειά της
με τη βοήθειά της 

 οποιαδήποτε 1-1, επί, γνησίως αύξουσα και συνεχή συνάρτηση.
οποιαδήποτε 1-1, επί, γνησίως αύξουσα και συνεχή συνάρτηση. , επαγωγικά, μπορούμε να αποδείξουμε τον ακόλουθο ισχυρισμό:
, επαγωγικά, μπορούμε να αποδείξουμε τον ακόλουθο ισχυρισμό:
 με
με 
 και
και 
 ορίζουμε τη συνάρτηση
ορίζουμε τη συνάρτηση  με
με  στο
στο  για κάθε
για κάθε  και η οποία θα είναι 1-1, επί, γνησίως αύξουσα, συνεχής και θα έχει τις ιδιότητες
και η οποία θα είναι 1-1, επί, γνησίως αύξουσα, συνεχής και θα έχει τις ιδιότητες  για κάθε
για κάθε 
 για κάθε
για κάθε 
 και για την επί, 1-1, γνησίως αύξουσα, συνεχή συνάρτηση
και για την επί, 1-1, γνησίως αύξουσα, συνεχή συνάρτηση 
 αν
αν  τότε
τότε  οπότε
οπότε 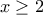
 στο σύνολο
στο σύνολο  θα ισχύει η ισότητα
θα ισχύει η ισότητα 
 για κάποιον φυσικό αριθμό
για κάποιον φυσικό αριθμό  , θα έχουμε
, θα έχουμε




 από την οποία θα προκύψει η ζητούμενη
από την οποία θα προκύψει η ζητούμενη  μπορούμε να λάβουμε περιορίζοντας την
μπορούμε να λάβουμε περιορίζοντας την  στο
στο 
 έχει ολοκληρωθεί.
έχει ολοκληρωθεί. 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης