Γιώργος Μήτσιος έγραψε:Θεωρούμε
τραπέζιο 
με

και φέρουμε

όπου

και

Να εντοπιστεί (με Γεωμετρική κατασκευή ) η θέση του

ώστε να ισχύει και


Έστω ότι έχουν βρεθεί τα σημεία

επί των πλευρών

αντιστοίχως, ώστε

και

και έστω το σημείο

Από


και από


Από
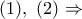



- Κατασκευή για διπλή παραλληλία.
- f=22_t=75360.PNG (17.95 KiB) Προβλήθηκε 329 φορές

Από

προκύπτει ότι το σημείο

κατασκευάζεται εύκολα ως εξής :
Γράφουμε το ημικύκλιο

με διάμετρο το τμήμα

και ας είναι

η εφαπτομένη του

από το σημείο

Το ζητούμενο σημείο

προσδιορίζεται ως το σημείο τομής της πλευράς

από τον κύκλο με κέντρο το σημείο

και ακτίνα

και άρα ισχύει η

Αποδεικνύεται εύκολα ότι ισχύει

όπου

ώστε
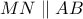
και το πρόβλημα έχει λυθεί.
Κώστας Βήττας.
 με
με  και φέρουμε
και φέρουμε 
 και
και 
 ώστε να ισχύει και
ώστε να ισχύει και 

 Προφανώς οι πράσινες γωνίες είναι ίσες, όπως και οι κόκκινες.
Προφανώς οι πράσινες γωνίες είναι ίσες, όπως και οι κόκκινες.  είναι όμοια, καθώς επίσης και τα
είναι όμοια, καθώς επίσης και τα 
 οπότε
οπότε 
 όπου
όπου 

 Έστω ότι έχουν βρεθεί τα σημεία
Έστω ότι έχουν βρεθεί τα σημεία  επί των πλευρών
επί των πλευρών  αντιστοίχως, ώστε
αντιστοίχως, ώστε  και
και 


 και από
και από 

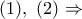


 προκύπτει ότι το σημείο
προκύπτει ότι το σημείο  κατασκευάζεται εύκολα ως εξής :
κατασκευάζεται εύκολα ως εξής : με διάμετρο το τμήμα
με διάμετρο το τμήμα  και ας είναι
και ας είναι  η εφαπτομένη του
η εφαπτομένη του 
 από τον κύκλο με κέντρο το σημείο
από τον κύκλο με κέντρο το σημείο  και ακτίνα
και ακτίνα  και άρα ισχύει η
και άρα ισχύει η 
 όπου
όπου  ώστε
ώστε 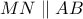 και το πρόβλημα έχει λυθεί.
και το πρόβλημα έχει λυθεί.
 και
και  .
. και φέρουμε
και φέρουμε  . Τότε ισχύουν
. Τότε ισχύουν 
 βασισμένος στην ισότητα
βασισμένος στην ισότητα  στην λύση του Γιώργου πιο πάνω (#2), είναι η εξής :
στην λύση του Γιώργου πιο πάνω (#2), είναι η εξής : ώστε το
ώστε το  να είναι παραλληλόγραμμο
να είναι παραλληλόγραμμο 
 και
και 
 και ας είναι
και ας είναι 
 τέμνει το ημικύκλιο
τέμνει το ημικύκλιο  και ας είναι
και ας είναι  το σημείο τομής της
το σημείο τομής της  και ακτίνα
και ακτίνα 
 παράλληλη ευθεία προς την
παράλληλη ευθεία προς την  τέμνει την
τέμνει την  στο σημείο
στο σημείο 
 όπου
όπου