ΑΣΚΗΣΗ 1
Δίνεται η συνάρτηση
![f:[a,b] \rightarrow (0, + \infty) f:[a,b] \rightarrow (0, + \infty)](/forum/ext/geomar/texintegr/latexrender/pictures/7489f26c582b0537d00d75151aaa8394.png) , συνεχής στο
, συνεχής στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) . Να αποδείξετε ότι για κάθε
. Να αποδείξετε ότι για κάθε ![x_{1},x_{2},x_{3} \in [a,b] x_{1},x_{2},x_{3} \in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/ed2674f1ab1a27d6a8606c2e272cbcb6.png) , υπάρχει
, υπάρχει ![x_{0} \in[a,b] x_{0} \in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/bb3fb9d05e1febc14daf2aeba148070c.png) τέτοιο, ώστε
τέτοιο, ώστε ![f(x_{0})= \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})} f(x_{0})= \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})}](/forum/ext/geomar/texintegr/latexrender/pictures/dcef6a9eb8334dd8f452bda0e3b62b1b.png)
Συντονιστής: Καρδαμίτσης Σπύρος
![f:[a,b] \rightarrow (0, + \infty) f:[a,b] \rightarrow (0, + \infty)](/forum/ext/geomar/texintegr/latexrender/pictures/7489f26c582b0537d00d75151aaa8394.png) , συνεχής στο
, συνεχής στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) . Να αποδείξετε ότι για κάθε
. Να αποδείξετε ότι για κάθε ![x_{1},x_{2},x_{3} \in [a,b] x_{1},x_{2},x_{3} \in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/ed2674f1ab1a27d6a8606c2e272cbcb6.png) , υπάρχει
, υπάρχει ![x_{0} \in[a,b] x_{0} \in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/bb3fb9d05e1febc14daf2aeba148070c.png) τέτοιο, ώστε
τέτοιο, ώστε ![f(x_{0})= \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})} f(x_{0})= \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})}](/forum/ext/geomar/texintegr/latexrender/pictures/dcef6a9eb8334dd8f452bda0e3b62b1b.png)
 είναι συνεχής και ορισμένη σε κλειστό διάστημα, άρα θα παίρνει μια μέγιστη τιμή
είναι συνεχής και ορισμένη σε κλειστό διάστημα, άρα θα παίρνει μια μέγιστη τιμή  και μια ελάχιστη
και μια ελάχιστη 
 για κάθε
για κάθε  που ανήκει στο πεδίο ορισμού της.
που ανήκει στο πεδίο ορισμού της. τις τιμές προκύπτει
τις τιμές προκύπτει
![m \leq \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})} \leq M m \leq \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})} \leq M](/forum/ext/geomar/texintegr/latexrender/pictures/4bbfc2bd3f9bb4c8524380a19602e69f.png)


![f(x_{0})= \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})} f(x_{0})= \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})}](/forum/ext/geomar/texintegr/latexrender/pictures/dcef6a9eb8334dd8f452bda0e3b62b1b.png)
 είναι σταθερή, εύκολα φαίνεται πως ισχύει το ζητούμενο.
είναι σταθερή, εύκολα φαίνεται πως ισχύει το ζητούμενο. . Αν η
. Αν η  είναι γνησίως αύξουσα και κυρτή στο
είναι γνησίως αύξουσα και κυρτή στο  , τότε, να δείξετε ότι υπάρχει, τουλάχιστον ένα,
, τότε, να δείξετε ότι υπάρχει, τουλάχιστον ένα,  τέτοιο ώστε
τέτοιο ώστε  .
.Θεωρώ συνάρτησηM.S.Vovos έγραψε:Ας συμπληρώσω και γω μια άσκηση, στην ωραία προσπάθεια του Λάμπρου!
ΑΣΚΗΣΗ 2
Έστω η δύο φορές παραγωγίσιμη συνάρτηση. Αν η
είναι γνησίως αύξουσα και κυρτή στο
, τότε, να δείξετε ότι υπάρχει, τουλάχιστον ένα,
τέτοιο ώστε
.



 αφού
αφού γν. αύξουσα.
γν. αύξουσα.
![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) και
και![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) υπάρχουν ξ1,ξ2 ώστε
υπάρχουν ξ1,ξ2 ώστε και
και Αφού η
Αφού η  είναι κυρτή, η
είναι κυρτή, η θα είναι γν. αύξουσα.
θα είναι γν. αύξουσα.

 ώστε να ικανοποιείται το ζητούμενο.
ώστε να ικανοποιείται το ζητούμενο.Προσοχή!!!papamixalis έγραψε:Καλησπέρα.
Άρα από Θ.Ε.Τ. θα υπάρχει
ώστε
Φιλικά
Μιχάλης
 , ώστε
, ώστε  , για κάθε
, για κάθε  και
και  .
. και να τη μελετήσετε ως προς τη μονοτονία.
και να τη μελετήσετε ως προς τη μονοτονία. και το σύνολο τιμών της.
και το σύνολο τιμών της. είναι αδύνατη στο
είναι αδύνατη στο  , να δείξετε ότι
, να δείξετε ότι  .
. , με
, με  , να δείξετε ότι
, να δείξετε ότι 
Λάμπρος Μπαλός έγραψε:ΑΣΚΗΣΗ 3
Εστω η παραγωγίσιμη συνάρτηση, ώστε
, για κάθε
και
.
Α) Να δείξετε ότικαι να τη μελετήσετε ως προς τη μονοτονία.
Β) Να βρείτε τις ασύμπτωτες τηςκαι το σύνολο τιμών της.
Γ) Αν η εξίσωσηείναι αδύνατη στο
, να δείξετε ότι
.
Δ) Αν, με
, να δείξετε ότι
 , τότε για κάθε
, τότε για κάθε  , ισχύει :
, ισχύει : . ( Η ανισότητα αυτή σας είναι γνωστή , απαιτείται όμως απόδειξη ) .
. ( Η ανισότητα αυτή σας είναι γνωστή , απαιτείται όμως απόδειξη ) . .
. και
και  ,
, 
ΚαλησπέραΛάμπρος Μπαλός έγραψε:ΑΣΚΗΣΗ 3
Εστω η παραγωγίσιμη συνάρτηση, ώστε
, για κάθε
και
.
Α) Να δείξετε ότικαι να τη μελετήσετε ως προς τη μονοτονία.
Β) Να βρείτε τις ασύμπτωτες τηςκαι το σύνολο τιμών της.
Γ) Αν η εξίσωσηείναι αδύνατη στο
, να δείξετε ότι
.
Δ) Αν, με
, να δείξετε ότι

 στο 0 από τα δεξιά είναι + άπειρο άρα η
στο 0 από τα δεξιά είναι + άπειρο άρα η  κατακόρυφη ασύμπτωτη.
κατακόρυφη ασύμπτωτη. στο + άπειρο κάνει
στο + άπειρο κάνει  , αλλά το όριο της
, αλλά το όριο της  στο + άπειρο κάνει + άπειρο.Άρα η
στο + άπειρο κάνει + άπειρο.Άρα η  δεν έχει πλάγια ασύμπτωτη.
δεν έχει πλάγια ασύμπτωτη. ισχύει.
ισχύει. και
και  άρα δεν είναι αδύνατη για κάθε χ.
άρα δεν είναι αδύνατη για κάθε χ.
 και προσθέτω τα
και προσθέτω τα  .
. που ισχύει αφού το
που ισχύει αφού το  είναι το ελάχιστο της
είναι το ελάχιστο της  και η ισότητα ισχύει μόνο για
και η ισότητα ισχύει μόνο για  που δεν ισχύει.
που δεν ισχύει.

 και
και 
 αδύνατη
αδύνατη  διότι για
διότι για 



 συνάρτηση
συνάρτηση  , με
, με  και η συνεχής στο
και η συνεχής στο  συνάρτηση
συνάρτηση  , με
, με  , για κάθε
, για κάθε  . Αν ισχύει
. Αν ισχύει  , για κάθε
, για κάθε  , να δείξετε ότι
, να δείξετε ότι  , για κάθε
, για κάθε  .
.KARKAR έγραψε:Άσκηση 4
α) Δείξτε ότι αν μια συνάρτηση είναι κυρτή σ' ένα διάστημα, τότε για κάθε
, ισχύει :
. ( Η ανισότητα αυτή σας είναι γνωστή , απαιτείται όμως απόδειξη ) .
β) Εξετάστε ως προς την κυρτότητα τη συνάρτηση.
γ) Συγκρίνατε τους αριθμούς :και
,
![[a,\dfrac{a+b}{2}] [a,\dfrac{a+b}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/0c4dfeb0e1697f3336819ed20a10278e.png) και
και ![[\dfrac{a+b}{2},b] [\dfrac{a+b}{2},b]](/forum/ext/geomar/texintegr/latexrender/pictures/4992903c45ecd237771303ea3ed8a347.png)
 είναι κυρτή.
είναι κυρτή.
 άρα η
άρα η  είναι κυρτή.
είναι κυρτή.
 και δεξιά το
και δεξιά το 
 είναι συνεχής στα
είναι συνεχής στα  και
και  και ισχύουν :
και ισχύουν : ,
,  (1) και
(1) και 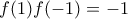
 διατηρεί πρόσημο σε καθένα από τα διαστήματα
διατηρεί πρόσημο σε καθένα από τα διαστήματα  και
και 
 είναι
είναι  στο πεδίο ορισμού της .
στο πεδίο ορισμού της . η εξίσωση
η εξίσωση 

 είναι περιττή στο
είναι περιττή στο  , να δείξετε ότι
, να δείξετε ότι 
 με
με  , για την οποία ισχύει
, για την οποία ισχύει  , για κάθε
, για κάθε  .
. .
. ισχύει
ισχύει  .
. τέτοιο, ώστε
τέτοιο, ώστε  .
. ώστε το εμβαδόν του χωρίου, που περικλείεται από τη
ώστε το εμβαδόν του χωρίου, που περικλείεται από τη  και τις ευθείες
και τις ευθείες  και
και  , να γίνεται ελάχιστο.
, να γίνεται ελάχιστο. για την οποία ισχύει:
για την οποία ισχύει: , για κάθε
, για κάθε  .
. και
και 
![x_{0} \in [0,1] x_{0} \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/fd977bc281951fdc9e7c5de4f4401317.png) τέτοιο, ώστε
τέτοιο, ώστε 
 είναι παραγωγίσιμη και
είναι παραγωγίσιμη και  , για κάθε
, για κάθε 
 και να γράψετε την εξίσωση εφαπτομένης της
και να γράψετε την εξίσωση εφαπτομένης της  στο σημείο της με τετμημένη
στο σημείο της με τετμημένη  .
.
A)Λάμπρος Μπαλός έγραψε:ΑΣΚΗΣΗ 6
Η συνάρτησηείναι συνεχής στα
και
και ισχύουν :
,
(1) και
Α) Να δείξετε ότι ηδιατηρεί πρόσημο σε καθένα από τα διαστήματα
και
Β) Να δείξετε ότι ηείναι
στο πεδίο ορισμού της .
Γ) Να λυθεί στοη εξίσωση
Δ) Να δείξετε ότι δεν υπάρχει το
Ε) Αν ηείναι περιττή στο
, να δείξετε ότι

 που σημαίνει ότι στα υποδιαστήματα
που σημαίνει ότι στα υποδιαστήματα  και
και  του πεδίου ορισμού της όχι μόνο διατηρεί πρόσημο αλλά και είναι αυτό διαφορετικό.
του πεδίου ορισμού της όχι μόνο διατηρεί πρόσημο αλλά και είναι αυτό διαφορετικό.

 απορρίπτεται καθώς από τα συμπεράσματα του ερωτήματος Α)
απορρίπτεται καθώς από τα συμπεράσματα του ερωτήματος Α)  και σε καμιά περίπτωση ίσα μεταξύ τους.
και σε καμιά περίπτωση ίσα μεταξύ τους.



 είτε μη πεπερασμένο
είτε μη πεπερασμένο 
 τότε
τότε  καθώς η
καθώς η  είναι συνεχής και ορίζεται η σύνθεση της για κάθε τιμή του πεδίου ορισμού της.
είναι συνεχής και ορίζεται η σύνθεση της για κάθε τιμή του πεδίου ορισμού της. άτοπο.
άτοπο. άρα
άρα  σε μια περιοχή εκατέρωθεν του μηδενός, άτοπο.
σε μια περιοχή εκατέρωθεν του μηδενός, άτοπο.

 περιττή συνάρτηση
περιττή συνάρτηση
Ένας άλλος τρόπος:papamixalis έγραψε:Καλησπέρα.
Πολύ ωραία πρωτοβουλία.
Ηείναι συνεχής και ορισμένη σε κλειστό διάστημα, άρα θα παίρνει μια μέγιστη τιμή
και μια ελάχιστη
άρα θα ισχύει
για κάθε
που ανήκει στο πεδίο ορισμού της.
Βάζοντας όπουτις τιμές προκύπτει
(1)
όπου
 προκύπτει ότι ο αριθμός
προκύπτει ότι ο αριθμός ![\sqrt[3]{f(x_{1})f(x_{2})f(x_{3})} \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})}](/forum/ext/geomar/texintegr/latexrender/pictures/96812708a4c19a38ce32b505589d0f9f.png) ανήκει στο σύνολο τιμών της
ανήκει στο σύνολο τιμών της  , οπότε υπάρχει
, οπότε υπάρχει ![x_{0} \in[a,b] x_{0} \in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/bb3fb9d05e1febc14daf2aeba148070c.png) τέτοιο, ώστε
τέτοιο, ώστε ![f(x_{0})= \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})} f(x_{0})= \sqrt[3]{f(x_{1})f(x_{2})f(x_{3})}](/forum/ext/geomar/texintegr/latexrender/pictures/dcef6a9eb8334dd8f452bda0e3b62b1b.png)
Γ1)Λάμπρος Μπαλός έγραψε:ΑΣΚΗΣΗ 8 (Γ Θέμα της Ο.Ε.Φ.Ε 2011)
Εστω μια συνεχής συνάρτησηγια την οποία ισχύει:
, για κάθε
.
Γ1) Να αποδείξετε ότι :
i)και
ii) Υπάρχειτέτοιο, ώστε
Γ2) Εστω, επιπλέον ότι ηείναι παραγωγίσιμη και
, για κάθε
i) Να βρείτε τοκαι να γράψετε την εξίσωση εφαπτομένης της
στο σημείο της με τετμημένη
.
ii) Να υπολογίσετε το όριο


![\displaystyle{g\left( x \right) = f\left( x \right) + x - 1,x \in \left[ {0,1} \right]} \displaystyle{g\left( x \right) = f\left( x \right) + x - 1,x \in \left[ {0,1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/515436efe7b97c16e03eafa4d3d1e97a.png) η οποία είναι συνεχής ως πράξεις συνεχών συναρτήσεων.
η οποία είναι συνεχής ως πράξεις συνεχών συναρτήσεων. διακρίνουμε περιπτώσεις:
διακρίνουμε περιπτώσεις:
 ή
ή 
 ικανοποιούνται οι υποθέσεις του θεωρήματος Bolzano συνεπώς υπάρχει τουλάχιστον ένα
ικανοποιούνται οι υποθέσεις του θεωρήματος Bolzano συνεπώς υπάρχει τουλάχιστον ένα 
![\displaystyle{{x_0} \in \left[ {0,1} \right]:g\left( {{x_0}} \right) = 0 \Rightarrow f\left( {{x_0}} \right) + {x_0} = 1} \displaystyle{{x_0} \in \left[ {0,1} \right]:g\left( {{x_0}} \right) = 0 \Rightarrow f\left( {{x_0}} \right) + {x_0} = 1}](/forum/ext/geomar/texintegr/latexrender/pictures/a3740f80bc4250c9fda345f76f059af5.png)
 , άρα για την παραγωγίσιμη συνάρτηση
, άρα για την παραγωγίσιμη συνάρτηση  γνωρίζουμε ότι
γνωρίζουμε ότι . Συνεπώς σε εσωτερικό σημείο του πεδίου ορισμού της παρουσιάζει ακρότατο (ολικό ελάχιστο) σύμφωνα με το θεώρημα Fermat
. Συνεπώς σε εσωτερικό σημείο του πεδίου ορισμού της παρουσιάζει ακρότατο (ολικό ελάχιστο) σύμφωνα με το θεώρημα Fermat 


Άλλος ένας τρόπος για κάποιον που δεν θα σκεφτεί τον μακαρίτη τον Fermat...Λάμπρος Μπαλός έγραψε: Γ2) Εστω, επιπλέον ότι ηείναι παραγωγίσιμη και
, για κάθε
i) Να βρείτε τοκαι να γράψετε την εξίσωση εφαπτομένης της
στο σημείο της με τετμημένη
.

 παραγωγίσιμη στο
παραγωγίσιμη στο  οπότε,
οπότε,
 (
( )
) ,
,  (
( )
) ),(
),( ) έχουμε ότι
) έχουμε ότι 
Καλησπέρα σε όλους.M.S.Vovos έγραψε:ΆΣΚΗΣΗ 7
Έστω η παραγωγίσιμη συνάρτησημε
, για την οποία ισχύει
, για κάθε
.
Α. Να βρείτε τον τύπο της συνάρτησης.
B. Να δείξετε ότι για κάθεισχύει
.
Γ. Να δείξετε ότι υπάρχει τουλάχιστον ένα,τέτοιο, ώστε
.
Δ. Να βρείτε τον πραγματικό αριθμόώστε το εμβαδόν του χωρίου, που περικλείεται από τη
και τις ευθείες
και
, να γίνεται ελάχιστο.
Φιλκά,
Μάριος



 άρα
άρα  για
για 
 και έπειτα λογαριθμίζω.
και έπειτα λογαριθμίζω. ώστε
ώστε  να μας δίνει αυτό που υπάρχει ενδιάμεσα.
να μας δίνει αυτό που υπάρχει ενδιάμεσα. και
και  γν άυξουσα.
γν άυξουσα. και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε.


 ώστε
ώστε
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες