Αρχιμήδης Καλή επιτυχία.
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
- S.E.Louridas
- Δημοσιεύσεις: 6141
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Αρχιμήδης Καλή επιτυχία.
Εύχομαι στους διαγωνιζόμενους στην φάση του διαγωνισμού Αρχιμήδης ΚΑΛΗ ΕΠΙΤΥΧΙΑ
Όταν κάνει ζέστη τότε αυτόματα το σώμα μας ιδρώνει, ναι είναι αυτόματη κίνηση και ΔΕΝ πρέπει να φοβόμαστε μήπως δεν ιδρώσουμε.
Έτσι και όταν είμαστε δίπλα από ένα Μαθηματικό Πρόβλημα να είμαστε σίγουροι ότι η αυτόματη κίνηση είναι ο σκληρός δίσκος του εγκεφάλου μας να στείλει τις κατάλληλες γνώσεις μας (πόσες φορές δεν έχουμε αναρωτηθεί: βρε πώς μούρθε αυτό;). Η μόνη ΠΙΘΑΝΗ περίπτωση αναστολής αυτού του αυτόματου μηχανισμού είναι να φοβηθούμε μήπως κάτι από αυτά που γνωρίζουμε δεν μας έρθει την στιγμή αυτή.
Αρα πάμε στον Διαγωνισμό χωρίς ψυχολογικές Αναστολές χωρίς φόβο και μάλιστα με την απόλυτη σιγουριά, ότι από μόνο του το μυαλό μας θα στείλει αυτό που πρέπει τη κατάλληλη στιγμή.
S.E.Louridas
Όταν κάνει ζέστη τότε αυτόματα το σώμα μας ιδρώνει, ναι είναι αυτόματη κίνηση και ΔΕΝ πρέπει να φοβόμαστε μήπως δεν ιδρώσουμε.
Έτσι και όταν είμαστε δίπλα από ένα Μαθηματικό Πρόβλημα να είμαστε σίγουροι ότι η αυτόματη κίνηση είναι ο σκληρός δίσκος του εγκεφάλου μας να στείλει τις κατάλληλες γνώσεις μας (πόσες φορές δεν έχουμε αναρωτηθεί: βρε πώς μούρθε αυτό;). Η μόνη ΠΙΘΑΝΗ περίπτωση αναστολής αυτού του αυτόματου μηχανισμού είναι να φοβηθούμε μήπως κάτι από αυτά που γνωρίζουμε δεν μας έρθει την στιγμή αυτή.
Αρα πάμε στον Διαγωνισμό χωρίς ψυχολογικές Αναστολές χωρίς φόβο και μάλιστα με την απόλυτη σιγουριά, ότι από μόνο του το μυαλό μας θα στείλει αυτό που πρέπει τη κατάλληλη στιγμή.
S.E.Louridas
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: Αρχιμήδης Καλή επιτυχία.
Οι μαθητές που απλά έφτασαν στον αρχιμήδη θα βραβευτούν αύριο ή όχι ?
Κάρτας Κώστας
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4831
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
- S.E.Louridas
- Δημοσιεύσεις: 6141
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Αρχιμήδης Καλή επιτυχία.
Καλή επιτυχία και στην επιτροπή των εισηγητών των θεμάτων, που πρέπει να αναγνωρίσουμε ότι έχει δύσκολο πράγματι έργο.
Εύχομαι και πιστεύω τα θέματα να είναι καλά, πρωτότυπα και πάντως να είναι θέματα που να δίνουν το σωστό στίγμα. Δεν είναι υποχρεωτικό να είναι άπιαστα.
Καλό θα είναι όποιος λάβει γνώση των θεμάτων, να τα ανεβάσει στο forum μας όσο το δυνατόν γρηγορότερα.
S.E.Louridas
Εύχομαι και πιστεύω τα θέματα να είναι καλά, πρωτότυπα και πάντως να είναι θέματα που να δίνουν το σωστό στίγμα. Δεν είναι υποχρεωτικό να είναι άπιαστα.
Καλό θα είναι όποιος λάβει γνώση των θεμάτων, να τα ανεβάσει στο forum μας όσο το δυνατόν γρηγορότερα.
S.E.Louridas
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
- S.E.Louridas
- Δημοσιεύσεις: 6141
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Αρχιμήδης Καλή επιτυχία.
Πρός το παρόν...Αναμονή.
Ίσως είναι αυτό που λέμε...το καλό πράγμα αργεί...
S.E.Louridas
Ίσως είναι αυτό που λέμε...το καλό πράγμα αργεί...
S.E.Louridas
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
-
mathfinder
- Διευθύνον Μέλος
- Δημοσιεύσεις: 524
- Εγγραφή: Πέμ Ιαν 01, 2009 11:56 pm
Re: Αρχιμήδης Καλή επιτυχία.
Ανεβάζω τα 3 από τα 4 θέματα των "μικρών" , με επιφύλαξη , γιατί μου μεταφέρθηκαν από το τηλέφωνο .
Θέματα των μικρών
1. Δίνεται οξυγώνιο τρίγωνο με
με  εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  . Ο κύκλος
. Ο κύκλος  τέμνει την
τέμνει την  στο
στο  και τον κύκλο
και τον κύκλο  στο
στο  . Να αποδείξετε ότι η
. Να αποδείξετε ότι η  διχοτομεί τη γωνία
διχοτομεί τη γωνία  .
.
2. Για τις διάφορες τιμές του ρητού να λυθεί η εξίσωση
να λυθεί η εξίσωση  .
.
3. Οι θετικοί ακέραιοι με
με  ικανοποιούν τη σχέση
ικανοποιούν τη σχέση  .
.
(α) Να δείξετε ότι ο διαιρεί το
διαιρεί το  .
.
(β) Αν επιπλέον ισχύει να βρείτε όλα τα ζεύγη
να βρείτε όλα τα ζεύγη  .
.
Καλά αποτελέσματα σε όλα τα παιδιά που διαγωνίστηκαν .
Αθ. Μπεληγιάννης
Θέματα των μικρών
1. Δίνεται οξυγώνιο τρίγωνο
 με
με  εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  . Ο κύκλος
. Ο κύκλος  τέμνει την
τέμνει την  στο
στο  και τον κύκλο
και τον κύκλο  στο
στο  . Να αποδείξετε ότι η
. Να αποδείξετε ότι η  διχοτομεί τη γωνία
διχοτομεί τη γωνία  .
.2. Για τις διάφορες τιμές του ρητού
 να λυθεί η εξίσωση
να λυθεί η εξίσωση  .
.3. Οι θετικοί ακέραιοι
 με
με  ικανοποιούν τη σχέση
ικανοποιούν τη σχέση  .
. (α) Να δείξετε ότι ο
 διαιρεί το
διαιρεί το  .
.(β) Αν επιπλέον ισχύει
 να βρείτε όλα τα ζεύγη
να βρείτε όλα τα ζεύγη  .
.Καλά αποτελέσματα σε όλα τα παιδιά που διαγωνίστηκαν .
Αθ. Μπεληγιάννης
τελευταία επεξεργασία από mathfinder σε Σάβ Μαρ 03, 2012 5:34 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Never stop learning , because life never stops teaching.
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6584
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: Αρχιμήδης Καλή επιτυχία.
Μήπως είναι έτσι;mathfinder έγραψε: 3. Οι θετικοί ακέραιοιμε
ικανοποιούν τη σχέση
.
(α) Να δείξετε ότι οδιαιρείται από τον
.
Θανάσης Κοντογεώργης
-
mathfinder
- Διευθύνον Μέλος
- Δημοσιεύσεις: 524
- Εγγραφή: Πέμ Ιαν 01, 2009 11:56 pm
Re: Αρχιμήδης Καλή επιτυχία.
Σωστά ο  διαιρεί το
διαιρεί το  . Λάθος μου στο γράψιμο , το διορθώνω .Ευχαριστώ για τη διόρθωση.
. Λάθος μου στο γράψιμο , το διορθώνω .Ευχαριστώ για τη διόρθωση.
Αθ. Μπεληγιάννης
 διαιρεί το
διαιρεί το  . Λάθος μου στο γράψιμο , το διορθώνω .Ευχαριστώ για τη διόρθωση.
. Λάθος μου στο γράψιμο , το διορθώνω .Ευχαριστώ για τη διόρθωση.Αθ. Μπεληγιάννης
Never stop learning , because life never stops teaching.
-
mathfinder
- Διευθύνον Μέλος
- Δημοσιεύσεις: 524
- Εγγραφή: Πέμ Ιαν 01, 2009 11:56 pm
Re: Αρχιμήδης Καλή επιτυχία.
Τα δύο θέματα των "μεγάλων"
1. Δύο θετικοί ακέραιοι που είναι πρώτοι μεταξύ τους, ικανοποιούν τη σχέση
που είναι πρώτοι μεταξύ τους, ικανοποιούν τη σχέση  , όπου
, όπου  θετικός ακέραιος , παράμετρος .
θετικός ακέραιος , παράμετρος .
Να βρείτε τα δυνατά ζεύγη .
.
2. Να προσδιορίσετε όλα τα μη μηδενικά πολυώνυμα με πραγματικούς συντελεστές του ελαχίστου δυνατού βαθμού τέτοια ώστε :
με πραγματικούς συντελεστές του ελαχίστου δυνατού βαθμού τέτοια ώστε :  .
.
Αθ. Μπεληγιάννης
1. Δύο θετικοί ακέραιοι
 που είναι πρώτοι μεταξύ τους, ικανοποιούν τη σχέση
που είναι πρώτοι μεταξύ τους, ικανοποιούν τη σχέση  , όπου
, όπου  θετικός ακέραιος , παράμετρος .
θετικός ακέραιος , παράμετρος . Να βρείτε τα δυνατά ζεύγη
 .
.2. Να προσδιορίσετε όλα τα μη μηδενικά πολυώνυμα
 με πραγματικούς συντελεστές του ελαχίστου δυνατού βαθμού τέτοια ώστε :
με πραγματικούς συντελεστές του ελαχίστου δυνατού βαθμού τέτοια ώστε :  .
.Αθ. Μπεληγιάννης
Never stop learning , because life never stops teaching.
-
dimitris.ligonis
- Δημοσιεύσεις: 103
- Εγγραφή: Πέμ Μάιος 12, 2011 11:55 am
Re: Αρχιμήδης Καλή επιτυχία.
Εντόπισα ένα λάθος στη λύση.Θα το διορθώσω και θα επανέλθω
τελευταία επεξεργασία από dimitris.ligonis σε Σάβ Μαρ 03, 2012 8:19 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Δημήτρης
- konstantinos21
- Δημοσιεύσεις: 19
- Εγγραφή: Σάβ Νοέμ 20, 2010 9:43 pm
-
mathfinder
- Διευθύνον Μέλος
- Δημοσιεύσεις: 524
- Εγγραφή: Πέμ Ιαν 01, 2009 11:56 pm
Re: Αρχιμήδης Καλή επιτυχία.
Το τρίτο θέμα των "μεγάλων" (Γεωμετρία)
3. Έστω οξυγώνιο τρίγωνο με
με  , εγγεγραμμένο στον κύκλο
, εγγεγραμμένο στον κύκλο  και η διχοτόμος
και η διχοτόμος 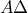 τέμνει τον κύκλο
τέμνει τον κύκλο  στο σημείο
στο σημείο  . O κύκλος
. O κύκλος  έχει κέντρο
έχει κέντρο  πάνω στην
πάνω στην  , διέρχεται από τα σημεία
, διέρχεται από τα σημεία  και τέμνει την
και τέμνει την  στο
στο  και την
και την  στο
στο  . Αν
. Αν 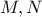 είναι τα μέσα των
είναι τα μέσα των  αντίστοιχα , να δείξετε ότι :
αντίστοιχα , να δείξετε ότι :
(α) οι ευθείες συντρέχουν σε κάποιο σημείο
συντρέχουν σε κάποιο σημείο  ,
,
(β) οι ευθείες συντρέχουν σε κάποιο σημείο
συντρέχουν σε κάποιο σημείο  ,
,
(γ) η είναι μεσοκάθετος της
είναι μεσοκάθετος της  .
.
Αθ. Μπεληγιάννης
3. Έστω οξυγώνιο τρίγωνο
 με
με  , εγγεγραμμένο στον κύκλο
, εγγεγραμμένο στον κύκλο  και η διχοτόμος
και η διχοτόμος 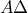 τέμνει τον κύκλο
τέμνει τον κύκλο  στο σημείο
στο σημείο  . O κύκλος
. O κύκλος  έχει κέντρο
έχει κέντρο  πάνω στην
πάνω στην  , διέρχεται από τα σημεία
, διέρχεται από τα σημεία  και τέμνει την
και τέμνει την  στο
στο  και την
και την  στο
στο  . Αν
. Αν 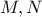 είναι τα μέσα των
είναι τα μέσα των  αντίστοιχα , να δείξετε ότι :
αντίστοιχα , να δείξετε ότι : (α) οι ευθείες
 συντρέχουν σε κάποιο σημείο
συντρέχουν σε κάποιο σημείο  ,
,(β) οι ευθείες
 συντρέχουν σε κάποιο σημείο
συντρέχουν σε κάποιο σημείο  ,
,(γ) η
 είναι μεσοκάθετος της
είναι μεσοκάθετος της  .
. Αθ. Μπεληγιάννης
Never stop learning , because life never stops teaching.
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6584
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: Αρχιμήδης Καλή επιτυχία.
Η σχέση γράφεταιmathfinder έγραψε: 2. Να προσδιορίσετε όλα τα μη μηδενικά πολυώνυμαμε πραγματικούς συντελεστές του ελαχίστου δυνατού βαθμού τέτοια ώστε :
.
 Το
Το  δε μπορεί να είναι σταθερό.
δε μπορεί να είναι σταθερό. Άρα το
 έχει βαθμό
έχει βαθμό  και βέβαια
και βέβαια  οπότε
οπότε 
Αν
 τότε
τότε  και από την ισότητα πολυωνύμων έχουμε άτοπο.
και από την ισότητα πολυωνύμων έχουμε άτοπο.Αν
 και
και  από την ισότητα πολυωνύμων είναι
από την ισότητα πολυωνύμων είναι 
Άρα
 και
και  όπου
όπου 
Θανάσης Κοντογεώργης
Re: Αρχιμήδης Καλή επιτυχία.
Κωνσταντίνος 21, με ποιό πρόγραμμα κάνεις τα σχήματα και γράφεις τα κείμενα? Θέλω να γράψω τη λύση του 3ου θέματος των μεγάλων και μου βγαίνει η ψυχή
mathfinder έγραψε:Τα δύο θέματα των "μεγάλων"
1. Δύο θετικοί ακέραιοιπου είναι πρώτοι μεταξύ τους, ικανοποιούν τη σχέση
, όπου
θετικός ακέραιος , παράμετρος .
Να βρείτε τα δυνατά ζεύγη.
2. Να προσδιορίσετε όλα τα μη μηδενικά πολυώνυμαμε πραγματικούς συντελεστές του ελαχίστου δυνατού βαθμού τέτοια ώστε :
.
Αθ. Μπεληγιάννης
Re: Αρχιμήδης Καλή επιτυχία.
Κωνσταντίνος 21, με ποιό πρόγραμμα κάνεις τα σχήματα και γράφεις τα κείμενα? Θέλω να γράψω τη λύση του 3ου θέματος των μεγάλων και μου βγαίνει η ψυχή
mathfinder έγραψε:Τα δύο θέματα των "μεγάλων"
1. Δύο θετικοί ακέραιοιπου είναι πρώτοι μεταξύ τους, ικανοποιούν τη σχέση
, όπου
θετικός ακέραιος , παράμετρος .
Να βρείτε τα δυνατά ζεύγη.
2. Να προσδιορίσετε όλα τα μη μηδενικά πολυώνυμαμε πραγματικούς συντελεστές του ελαχίστου δυνατού βαθμού τέτοια ώστε :
.
Αθ. Μπεληγιάννης
Re: Αρχιμήδης Καλή επιτυχία.
για το 2ο τον μεγάλων..την ίδα λύση με τον socrates έχουμε..
μια ερώτηση...
γι το πρωτο θεμα//
αφού
έπεται ότι και
και ![p=q-1] p=q-1]](/forum/ext/geomar/texintegr/latexrender/pictures/1778c7a4600c3fb76403d9cdd8e5ec1f.png) ??
??
Με συγχωρείτε για τη μη χρήση LATEX αλλά είμαι μέσω κινητού...
μια ερώτηση...
γι το πρωτο θεμα//
αφού

έπεται ότι
 και
και ![p=q-1] p=q-1]](/forum/ext/geomar/texintegr/latexrender/pictures/1778c7a4600c3fb76403d9cdd8e5ec1f.png) ??
??Με συγχωρείτε για τη μη χρήση LATEX αλλά είμαι μέσω κινητού...
τελευταία επεξεργασία από nsmavrogiannis σε Σάβ Μαρ 03, 2012 8:15 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λόγος: Διόρθωση κώδικα $ LaTeX$
Λόγος: Διόρθωση κώδικα $ LaTeX$
-
Grigoris K.
- Δημοσιεύσεις: 926
- Εγγραφή: Κυρ Μαρ 27, 2011 8:12 pm
Re: Αρχιμήδης Καλή επιτυχία.
Καλησπέραmathfinder έγραψε:Το τρίτο θέμα των "μεγάλων" (Γεωμετρία)
3. Έστω οξυγώνιο τρίγωνομε
, εγγεγραμμένο στον κύκλο
και η διχοτόμος
τέμνει τον κύκλο
στο σημείο
. O κύκλος
έχει κέντρο
πάνω στην
, διέρχεται από τα σημεία
και τέμνει την
στο
και την
στο
. Αν
είναι τα μέσα των
αντίστοιχα , να δείξετε ότι :
(α) οι ευθείεςσυντρέχουν σε κάποιο σημείο
,
(β) οι ευθείεςσυντρέχουν σε κάποιο σημείο
,
(γ) ηείναι μεσοκάθετος της
.
Αθ. Μπεληγιάννης
Φέρω
 και
και  .
. Είναι γνωστό ότι η
 είναι ισογώνια με την
είναι ισογώνια με την 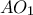 και η
και η  είναι ισογώνια με την
είναι ισογώνια με την  .
. Άρα αφού
 συνευθειακά, τα
συνευθειακά, τα  είναι επίσης συνευθειακά που συνεπάγεται ότι
είναι επίσης συνευθειακά που συνεπάγεται ότι  .
.Προκύπτει εύκολα ότι
 .
.Έστω
 . Οι προαναφερθείσες παραλληλίες δίνουν ότι το
. Οι προαναφερθείσες παραλληλίες δίνουν ότι το  είναι παρ/μο.
είναι παρ/μο.Άρα η
 διέρχεται από το
διέρχεται από το  επίσης. Το ζητούμενο δείχθηκε.
επίσης. Το ζητούμενο δείχθηκε. Ομοίως για το β) ερώτημα.
Το γ) είναι προφανές αφού
 .
.Re: Αρχιμήδης Καλή επιτυχία.
Για τους μεγάλους μια πολύ απλή και μικρή λύση στο 1 είναι όπως το βλέπω η εξής:
Η σχέση γράφεται και ως . Οπότε ισχύει
. Οπότε ισχύει  . Άρα αφού
. Άρα αφού  ,
,  . Αν
. Αν  τοτε θα έπρεπε
τοτε θα έπρεπε  , άτοπο. Άρα
, άτοπο. Άρα  και άμεσα
και άμεσα  .
.
Για το 2 τώρα αναρωτιέμαι πως και δεν ζητήθηκε (πχ σαν δεύτερο ερώτημα) η γενική λύση αφού με ευκλείδια διαίρεση του με το
με το  προκύπτει οτί αρκεί η ελαχίστου βαθμού περίπτωση.
προκύπτει οτί αρκεί η ελαχίστου βαθμού περίπτωση.
Kαλά αποτελέσματα.
Η σχέση γράφεται και ως
 . Οπότε ισχύει
. Οπότε ισχύει  . Άρα αφού
. Άρα αφού  ,
,  . Αν
. Αν  τοτε θα έπρεπε
τοτε θα έπρεπε  , άτοπο. Άρα
, άτοπο. Άρα  και άμεσα
και άμεσα  .
.Για το 2 τώρα αναρωτιέμαι πως και δεν ζητήθηκε (πχ σαν δεύτερο ερώτημα) η γενική λύση αφού με ευκλείδια διαίρεση του
 με το
με το  προκύπτει οτί αρκεί η ελαχίστου βαθμού περίπτωση.
προκύπτει οτί αρκεί η ελαχίστου βαθμού περίπτωση.Kαλά αποτελέσματα.
-
kwstas12345
- Δημοσιεύσεις: 1052
- Εγγραφή: Δευ Ιαν 11, 2010 2:12 pm
Re: Αρχιμήδης Καλή επιτυχία.
Άλλη μια λύση για το 1ο. Έυκολα βλέππουμε πώς πρέπει  , αντικαθιστώντας στην αρχική εύκολα παίρνουμε
, αντικαθιστώντας στην αρχική εύκολα παίρνουμε  και απαιτούμε αφού ο
και απαιτούμε αφού ο  είναι φυσικός
είναι φυσικός  αλλά και
αλλά και  άρα πρέπει
άρα πρέπει  και συνεπώς
και συνεπώς  .
.
Να ευχηθώ και γώ, καλά αποτελέσματα σε οσους διαγωνίστηκαν.
 , αντικαθιστώντας στην αρχική εύκολα παίρνουμε
, αντικαθιστώντας στην αρχική εύκολα παίρνουμε  και απαιτούμε αφού ο
και απαιτούμε αφού ο  είναι φυσικός
είναι φυσικός  αλλά και
αλλά και  άρα πρέπει
άρα πρέπει  και συνεπώς
και συνεπώς  .
.Να ευχηθώ και γώ, καλά αποτελέσματα σε οσους διαγωνίστηκαν.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
