 είναι ακέραιοι αριθμοί και
είναι ακέραιοι αριθμοί και  πολυώνυμο με ακέραιους συντελεστές τέτοιο ώστε να ισχύουν
πολυώνυμο με ακέραιους συντελεστές τέτοιο ώστε να ισχύουν  , να αποδείξετε οτι
, να αποδείξετε οτια) εαν ισχύει και
 , τότε το πολυώνυμο δεν έχει ρητή ρίζα
, τότε το πολυώνυμο δεν έχει ρητή ρίζαβ) εαν ισχύει και
 , τότε το πολυώνυμο, εαν έχει ρητή ρίζα, αυτή θα είναι ο αριθμός
, τότε το πολυώνυμο, εαν έχει ρητή ρίζα, αυτή θα είναι ο αριθμός  .
.Υπόδειξη: Στηριχτείτε στην πρόταση (την οποία να αποδείξετε) :
εαν
 ρητή ρίζα του πολυωνύμου
ρητή ρίζα του πολυωνύμου  και
και  ακέραιος, τότε ο ακέραιος
ακέραιος, τότε ο ακέραιος  διαιρεί τον ακέραιο
διαιρεί τον ακέραιο  .
.2. Σε επίπεδο
 θεωρούμε τραπέζιο
θεωρούμε τραπέζιο  με
με  .
.α) Έστω
 το μέσο του ευθυγράμμου τμήματος
το μέσο του ευθυγράμμου τμήματος  . Φέρνουμε την κάθετο του επιπέδου
. Φέρνουμε την κάθετο του επιπέδου  στο σημείο
στο σημείο  και πάνω της παίρνουμε το σημείο
και πάνω της παίρνουμε το σημείο  έτσι ώστε να είναι
έτσι ώστε να είναι  . Έστω
. Έστω  το σημείο του ευθυγράμμου τμήματος
το σημείο του ευθυγράμμου τμήματος  , για το οποίο ισχύει
, για το οποίο ισχύει  . Να ορισθεί επίπεδο
. Να ορισθεί επίπεδο  από το σημείο
από το σημείο  τέτοιο ώστε η στερεά γωνία
τέτοιο ώστε η στερεά γωνία  να τέμνεται από αυτό κατά παραλληλόγραμμο. Αν
να τέμνεται από αυτό κατά παραλληλόγραμμο. Αν  είναι τα σημεία τομής του
είναι τα σημεία τομής του  με τις
με τις  αντίστοιχα, να υπολογισθεί ο όγκος της πυραμίδας
αντίστοιχα, να υπολογισθεί ο όγκος της πυραμίδας  .
.β) Αν
 είναι τα σημεία των ευθυγράμμων τμημάτων
είναι τα σημεία των ευθυγράμμων τμημάτων  για τα οποία ισχύει οτι
για τα οποία ισχύει οτι  , να ορισθεί το επίπεδο δια της
, να ορισθεί το επίπεδο δια της  που είναι τέτοιο ώστε εαν
που είναι τέτοιο ώστε εαν  είναι τα σημεία τομής του με τις
είναι τα σημεία τομής του με τις  αντίστοιχα, η περίμετρος του τετραπλεύρου
αντίστοιχα, η περίμετρος του τετραπλεύρου  να είναι η ελάχιστη δυνατή.
να είναι η ελάχιστη δυνατή.γ) Να αποδείξετε οτι η πυραμίδα
 είναι εγγράψιμη σε σφαίρα.
είναι εγγράψιμη σε σφαίρα.3. Να βρεθούν τα ζεύγη
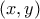 που ικανοποιούν την εξίσωση
που ικανοποιούν την εξίσωση  .
.