JBMO 2020

[Soteris]

Σήμερα είναι η μέρα του διαγωνισμού για την 24η Βαλκανική Μαθηματική Ολυμπιάδα Νέων, η οποία θα «τρέξει» εξ αποστάσεως. Να ευχηθώ ολόψυχα ότι καλύτερο στις εθνικές ομάδες Ελλάδας και Κύπρου.

Περισσότερες πληροφορίες και νέα για τον διαγωνισμό εδώ.

[Τσιαλας Νικολαος]

Καλή επιτυχία σε όλα τα παιδιά!!!

[george visvikis]

Καλή Επιτυχία στις αποστολές της Ελλάδας και της Κύπρου!

[cretanman]

Καλή επιτυχία σε όλους τους μαθητές μας και ιδιαίτερα της Ελλάδας και της Κύπρου! Συγχαρητήρια στο Δημήτρη Χριστοφίδη για το πρόβλημα 3 του διαγωνισμού!!

Τα θέματα:

Πρόβλημα 1 (Αλβανία)
Να βρεθούν όλες οι τριάδες πραγματικών αριθμών που αποτελούν λύση του συστήματος των εξισώσεων:

και




Πρόβλημα 2 (Θεόκλητος Παραγυιού - Κύπρος)
Δίνεται ορθογώνιο τρίγωνο με και το ίχνος της κάθετης από την κορυφή προς την πλευρά του τριγώνου. Δίνεται σημείο , διαφορετικό του σημείου , στην ευθεία , τέτοιο ώστε . Ονομάζουμε τον περιγεγραμμένο κύκλο στο τρίγωνο . Ο κύκλος και η τέμνονται ξανά στο σημείο και έστω το αντιδιαμετρικό σημείο του στον κύκλο . Οι ευθείες και τέμνονται στο σημείο . Αν η εφαπτομένη του κύκλου στο σημείο τέμνει την ευθεία στο σημείο , να αποδείξετε ότι τα σημεία είναι ομοκυκλικά.

Πρόβλημα 3 (Δημήτρης Χριστοφίδης - Κύπρος)
Η Αλίκη και ο Βασίλης παίζουν το παρακάτω παιγνίδι:
Η Αλίκη επιλέγει το σύνολο για κάποιον θετικό ακέραιο . Στη συνέχεια ξεκινώντας με τον Βασίλη διαλέγουν ο ένας μετά τον άλλο έναν αριθμό από το σύνολο σύμφωνα με τους παρακάτω κανόνες:
Αρχικά ο Βασίλης επιλέγει έναν οποιοδήποτε αριθμό, στη συνέχεια και σε κάθε επόμενο βήμα ο επιλεγμένος αριθμός πρέπει να είναι διαφορετικός από τους ήδη επιλεγμένους αριθμούς και πρέπει επίσης να διαφέρει κατά από έναν ήδη επιλεγμένο αριθμό. Το παιγνίδι τελειώνει όταν
έχουν επιλεγεί όλοι οι αριθμοί του συνόλου .
Η Αλίκη κερδίζει το παιγνίδι, όταν το άθροισμα των αριθμών που έχει επιλέξει είναι σύνθετος αριθμός, διαφορετικά κερδίζει ο Βασίλης το παιγνίδι.
Ποιος από τους δύο παίκτες έχει στρατηγική νίκης;

Πρόβλημα 4 (Αλβανία)
Να βρεθούν όλοι οι πρώτοι αριθμοί και έτσι ώστε ο αριθμός να είναι πρώτος.


Αλέξανδρος

[miltosk]

Καλή επιτυχία σε όλους τους μαθητές μας και ιδιαίτερα της Ελλάδας και της Κύπρου!
Πρόβλημα 4 (Αλβανία)

Να βρεθούν όλοι οι πρώτοι αριθμοί και έτσι ώστε ο αριθμός να είναι πρώτος.


Αλέξανδρος

Καλή επιτυχία σε όλα τα παιδιά και κυρίως στην Ελλάδα και την Κύπρο!!
Έχω βάλει λύση, έχει και άλλη, στο aops:https://artofproblemsolving.com/communi ... _problem_4

[cretanman]

Πρόβλημα 4 (Αλβανία)

Να βρεθούν όλοι οι πρώτοι αριθμοί και έτσι ώστε ο αριθμός να είναι πρώτος.


Αλέξανδρος

Η δική μου προσέγγιση στο θέμα:

Έστω , πρώτος. Τότε .

Παίρνοντας 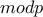και με τη βοήθεια του μικρού θεωρήματος του Fermat, εύκολα προκύπτει ότι και αφού , άρα . Έτσι λοιπόν,
και παίρνοντας , έχουμε τελικά άρα για κάποιο μη αρνητικό ακέραιο .

Λόγω της παίρνουμε άρα δηλαδή .

Όμως για και το 1ο μέλος είναι 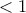αφού (εύκολο με επαγωγή επί του ). Άρα ή ή (που απορρίπτεται διότι τότε ο θα ήταν άρτιος μεγαλύτερος του ).

Αν τότε άρα απ' όπου (καθώς για είναι εύκολο να δείξουμε με επαγωγή ότι ). Άρα έχουμε τη λύση .

Αν τότε και τότε περίπτωση που απορρίπτεται αφού με επαγωγή είναι εύκολο να δειχθεί ότι κι έτσι το 1ο μέλος της είναι αρνητικό.

Αλέξανδρος

[Demetres]

Το δεύτερο είναι επίσης Κυπριακή πρόταση. Περιττό να αναφέρω τον δημιουργό.

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

Ο Θεόκλητος Παραγυιού ασφαλώς!

[S.E.Louridas]

Καλή Επιτυχία στους διαγωνιζόμενους από την Ελλάδα και από την Αδερφή μας Κύπρο.

[Μπάμπης Στεργίου]

Καλά αποτελέσματα στους μαθητές των Ελληνικών ομάδων

αλλά και σε όλους τους διαγωνιζόμενους !

[Ορέστης Λιγνός]

Πολλά συγχαρητήρια στην ομάδα μας στην JBMO 2020 για τις κορυφαίες επιδόσεις τους:

Πρόδρομος Φωτιάδης: 31/40, Χρυσό μετάλλιο
Κωνσταντίνος Κωνσταντινίδης: 31/40, Χρυσό Μετάλλιο
Γεώργιος Τζαχρήστας: 26/40, Αργυρό Μετάλλιο
Παναγιώτης Λιάμπας: 25/40, Αργυρό Μετάλλιο
Εμμανουήλ Πετράκης: 13/40, Χάλκινο Μετάλλιο
Στυλιανός Θέμελης: 11/40, Χάλκινο Μετάλλιο

Τα cut-offs των μεταλλίων ήταν 30, 20 και 8.

ΜΠΡΑΒΟ ΜΠΡΑΒΟ ΜΠΡΑΒΟ !!!

[cretanman]

Θερμά συγχαρητήρια σε όλη την ελληνική αποστολή καθώς και σε αρχηγό, υπαρχηγό για τις εξαιρετικές επιδόσεις των μαθητών μας (6 στα 6 μετάλλια) στη (διαδικτυακή) JBMO 2020.

Να σημειώσω επίσης ότι η Ελληνική Αποστολή κατέλαβε την 3η θέση με συνολικά 137 βαθμούς που είναι η καλύτερη θέση που έχει πετύχει σε αυτή τη διοργάνωση και βρίσκεται αμέσως μετά από τη Βουλγαρία (161 βαθμοί), Ρουμανία (157 βαθμοί) με μεγάλη μάλιστα διαφορά σε σχέση με ισχυρές δυνάμεις της διοργάνωσης (Τουρκία 109 βαθμοί και Σερβία 96 βαθμοί).

Αλέξανδρος Συγκελάκης

[Τσιαλας Νικολαος]

Πολλά μπράβο σε όλα τα παιδια!!

[Demetres]

Συγχαρητήρια στην Ελληνική αποστολή για την εξαιρετική επίδοση.

Η Κύπρος είχε τρία χάλκινα με τους

Φίλιππος-Άθως Χατζηχριστοφή (Filippos Athos) 17/40
Αρά Μαχτεσιάν 12/40
Κυριακή Άσσου 8/40

[miltosk]

Συγχαρητήρια στην ελληνική και στην κυπριακή αποστολή, καλή συνέχεια και εις ανώτερα σε όλα τα παιδιά!!! Πολλά συγχαρητήρια αξίζουν , επίσης,οι διοργανωτές, οι συνοδοί και όσοι συνέβαλαν στην πραγματοποίηση της JBMO 2020 αυτή την τόσο δύσκολη χρονιά.

[george visvikis]

Πολλά συγχαρητήρια στην ομάδα μας στην JBMO 2020 για τις κορυφαίες επιδόσεις τους:

Πρόδρομος Φωτιάδης: 31/40, Χρυσό μετάλλιο
Κωνσταντίνος Κωνσταντινίδης: 31/40, Χρυσό Μετάλλιο
Γεώργιος Τζαχρήστας: 26/40, Αργυρό Μετάλλιο
Παναγιώτης Λιάμπας: 25/40, Αργυρό Μετάλλιο
Εμμανουήλ Πετράκης: 13/40, Χάλκινο Μετάλλιο
Στυλιανός Θέμελης: 11/40, Χάλκινο Μετάλλιο

Τα cut-offs των μεταλλίων ήταν 30, 20 και 8.

ΜΠΡΑΒΟ ΜΠΡΑΒΟ ΜΠΡΑΒΟ !!!

Συγχαρητήρια σε όλα τα παιδιά!!!

[Doloros]

Θερμά συγχαρητήρια στα παιδιά και σε όλους που συνέβαλαν, με τον ένα ή τον άλλο τρόπο, στις επιτυχίες τους.

[Doloros]

Πρόβλημα 2 (Θεόκλητος Παραγυιού - Κύπρος)
Δίνεται ορθογώνιο τρίγωνο με και το ίχνος της κάθετης από την κορυφή προς την πλευρά του τριγώνου. Δίνεται σημείο , διαφορετικό του σημείου , στην ευθεία , τέτοιο ώστε . Ονομάζουμε τον περιγεγραμμένο κύκλο στο τρίγωνο . Ο κύκλος και η τέμνονται ξανά στο σημείο και έστω το αντιδιαμετρικό σημείο του στον κύκλο . Οι ευθείες και τέμνονται στο σημείο . Αν η εφαπτομένη του κύκλου στο σημείο τέμνει την ευθεία στο σημείο , να αποδείξετε ότι τα σημεία είναι ομοκυκλικά.

Μια υπόδειξη στο θέμα της Γεωμετρίας

Βαλκανιάδα Νέων 2020.png (50.76 KiB) Προβλήθηκε 2425 φορές

Οι ως κάθετες στην και αφού το μεν τετράπλευρο είναι παραλληλόγραμμο , το δε τετράπλευρο ισοσκελές τραπέζιο .

Η κόκκινη γωνία είναι ίση με κάθε κίτρινη , συνεπώς το τετράπλευρο είναι εγγράψιμο .

Άμεσες συνέπειες : η κι αυτή εφαπτομένη και οι πράσινες γωνίες ίσες .

Τα σημεία ανήκουν στο κύκλο διαμέτρου κι αφού το τετράπλευρο

είναι εγγράψιμο και τα πέντε σημεία: ανήκουν στον ίδιο κύκλο

[Μπάμπης Στεργίου]

Πολλά συγχαρητήρια στην ομάδα μας στην JBMO 2020 για τις κορυφαίες επιδόσεις τους:

Πρόδρομος Φωτιάδης: 31/40, Χρυσό μετάλλιο
Κωνσταντίνος Κωνσταντινίδης: 31/40, Χρυσό Μετάλλιο
Γεώργιος Τζαχρήστας: 26/40, Αργυρό Μετάλλιο
Παναγιώτης Λιάμπας: 25/40, Αργυρό Μετάλλιο
Εμμανουήλ Πετράκης: 13/40, Χάλκινο Μετάλλιο
Στυλιανός Θέμελης: 11/40, Χάλκινο Μετάλλιο

Τα cut-offs των μεταλλίων ήταν 30, 20 και 8.

ΜΠΡΑΒΟ ΜΠΡΑΒΟ ΜΠΡΑΒΟ !!!

Συγχαρητήρια σε όλα τα παιδιά !

Τους εύχομαι του χρόνου να πάρουν αντίστοιχα μετάλλια στην Βαλκανιάδα αλλά και στην ΙΜΟ !

[S.E.Louridas]

Το "οδοιπορικό" που οδηγεί στην συμμετοχή σε τέτοιους διαγωνισμούς είναι από μόνο του μία ηχηρή απάντηση στην πρόκληση της εποχής που σηματοδοτεί. Συγχαρητήρια πολλά και ειλικρινή στους τροπαιούχους στην jbmo μικρούς στην ηλικία αλλά τεράστιους Έλληνες συναδέλφους και στους γονείς τους. Η επιτυχία αυτή τους ανήκει ολοκληρωτικά, αποκλειστικά και δικαιωματικά, κάτι που δεν πρέπει να ξεχνούν ποτέ μα ποτέ στους παράξενους καιρούς μας. Θερμά και ειλικρινή επίσης συγχαρητήρια και στην ομάδα των Κυπρίων αδελφών μας. Καλή συνέχεια με Υγεία και Πρόοδο.