Γενικευμένα Ολοκληρώματα

vzf · #221

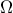Να αποδείξετε ότι $\displaystyle{\int_{-\infty}^{+\infty} \frac{dx}{ (e^x-x)^2 + \pi^2} = \frac{1}{1 + \Omega},}$ όπου $\Omega$ είναι η μοναδική πραγματική ρίζα της εξίσωσης e^xx=1.

Edit:εδώ

#222

vzf έγραψε: Να αποδείξετε ότι $\displaystyle{\int_{-\infty}^{+\infty} \frac{dx}{ (e^x-x)^2 + \pi^2} = \frac{1}{1 + \Omega},}$ όπου $\Omega$ είναι η μοναδική πραγματική ρίζα της εξίσωσης

Πανέμορφο

Επειδή $\displaystyle{\frac{1}{{{{\left( {{e^z} - z} \right)}^2} + {\pi ^2}}} = \frac{1}{{\left( {{e^z} - z - i\pi } \right)\left( {{e^z} - z + i\pi } \right)}} = \frac{1}{{2\pi i}}\left( {\frac{1}{{{e^z} - z - i\pi }} - \frac{1}{{{e^z} - z + i\pi }}} \right)}$ θα έχουμε:

$\displaystyle{\int\limits_{ - \infty }^{ + \infty } {\frac{1}{{{{\left( {{e^z} - z} \right)}^2} + {\pi ^2}}}dz} = \frac{1}{{2\pi i}}\left( {\int\limits_{ - \infty }^{ + \infty } {\frac{1}{{{e^z} - z - i\pi }}dz} - \int\limits_{ - \infty }^{ + \infty } {\frac{1}{{{e^z} - z + i\pi }}dz} } \right) = }$

$\displaystyle{ = \frac{1}{{2\pi i}}\left( {\int\limits_{ - \infty }^{ + \infty } {\frac{1}{{ - {e^{\left( {z + i\pi } \right)}} - \left( {z + i\pi } \right)}}dz} - \int\limits_{ - \infty }^{ + \infty } {\frac{1}{{ - {e^{\left( {z - i\pi } \right)}} - \left( {z - i\pi } \right)}}dz} } \right) = \frac{1}{{2\pi i}}\left( {\int\limits_{ - \infty + i\pi }^{ + \infty + i\pi } {\frac{1}{{ - {e^w} - w}}dw} - \int\limits_{ - \infty - i\pi }^{ + \infty - i\pi } {\frac{1}{{ - {e^w} - w}}dw} } \right) = }$

$\displaystyle{ = \frac{1}{{2\pi i}}\left( {\int\limits_{ - \infty - i\pi }^{ + \infty - i\pi } {\frac{1}{{{e^w} + w}}dw} - \int\limits_{ - \infty + i\pi }^{ + \infty + i\pi } {\frac{1}{{{e^w} + w}}dw} } \right) = \frac{1}{{2\pi i}}\left( {\int\limits_{ - \infty - i\pi }^{ + \infty - i\pi } {\frac{1}{{{e^w} + w}}dw} + \int\limits_{ + \infty + i\pi }^{ - \infty + i\pi } {\frac{1}{{{e^w} + w}}dw} } \right)}$ .

Όμως $\displaystyle{\left| {\frac{1}{{{e^w} + w}}} \right| \geqslant \frac{1}{{\left| {{e^w}} \right| + \left| w \right|}}\xrightarrow{{w \to \infty }}0}$ οπότε $\displaystyle{\int\limits_c {\frac{1}{{{e^w} + w}}dw} = \int\limits_{ - \infty - i\pi }^{ + \infty - i\pi } {\frac{1}{{{e^w} + w}}dw} + \int\limits_{ + \infty + i\pi }^{ - \infty + i\pi } {\frac{1}{{{e^w} + w}}dw} }$

όπου $\displaystyle{c:}$ το ορθογώνιο με κορυφές $\displaystyle{A\left( { - M, - \pi } \right),\;B\left( {M, - \pi } \right),\;C\left( {M,\pi } \right)\;\& \;D\left( { - M,\pi } \right)}$ με $\displaystyle{M \to + \infty }$ και με ορθή φορά περιστροφής.

Η συνάρτηση $\displaystyle{f\left( w \right) = \frac{1}{{{e^w} + w}}}$ είναι μερόμορφη στο εσωτερικό του ορθογωνίου $\displaystyle{c}$ (αναλυτική με κάποιους πόλους).

Αναζητάμε τους πόλους της $\displaystyle{f\left( w \right) = \frac{1}{{{e^w} + w}}}$ στο εσωτερικό του $\displaystyle{c}$ , επομένως τις ρίζες τις εξίσωσης $\displaystyle{{e^w} + w = 0}$ .

$\displaystyle{{e^w} + w = 0 \Rightarrow {e^{x + iy}} + x + iy = 0 \Rightarrow \left\{ {\begin{array}{*{20}{c}} \begin{gathered} {e^x}\cos y + x = 0 \hfill \\ \hfill \\ \end{gathered} \\ {{e^x}\sin y + y = 0} \\ \end{array} } \right.}$ Για $\displaystyle{y = 0}$ έχουμε ρίζα την μοναδική ρίζα της πραγματικής εξίσωσης $\displaystyle{{e^x} + x = 0}$ .

Για $\displaystyle{y \ne 0}$ έχουμε $\displaystyle{{e^x} = - \frac{y}{{\sin y}}}$ που είναι αδύνατη για $\displaystyle{y \in \left[ { - \pi ,\;\pi } \right]}$ (εντός του ορθογωνίου $\displaystyle{c}$ ). Άρα αν $\displaystyle{\rho :}$ η ρίζα της εξίσωσης $\displaystyle{{e^x} + x = 0}$ , θα έχουμε

$\displaystyle{\int\limits_c {\frac{1}{{{e^w} + w}}dw} = 2\pi i \cdot {\text{Res}}\left( {\frac{1}{{{e^w} + w}},w = \rho } \right) = 2\pi i \cdot \mathop {\lim }\limits_{w \to \rho } \frac{{w - \rho }}{{{e^w} + w}} = \frac{{2\pi i}}{{{e^\rho } + 1}}}$ ,

οπότε $\displaystyle{\int\limits_{ - \infty }^{ + \infty } {\frac{1}{{{{\left( {{e^z} - z} \right)}^2} + {\pi ^2}}}dz} = \frac{1}{{2\pi i}}\left( {\int\limits_{ - \infty - i\pi }^{ + \infty - i\pi } {\frac{1}{{{e^w} + w}}dw} + \int\limits_{ + \infty + i\pi }^{ - \infty + i\pi } {\frac{1}{{{e^w} + w}}dw} } \right) = \frac{1}{{2\pi i}}\int\limits_c {\frac{1}{{{e^w} + w}}dw} = \frac{1}{{{e^\rho } + 1}}}$

Όμως $\displaystyle{{e^\rho } + \rho = 0 \Rightarrow {e^\rho } = \left( { - \rho } \right) \Rightarrow \left( { - \rho } \right){e^{\left( { - \rho } \right)}} = 1}$ , δηλαδή $\displaystyle{ - \rho = \Omega }$ όπου $\displaystyle{\Omega :}$ η ρίζα της εξίσωσης $\displaystyle{x{e^x} = 1}$ .

Και τελικά $\displaystyle{\int\limits_{ - \infty }^{ + \infty } {\frac{1}{{{{\left( {{e^z} - z} \right)}^2} + {\pi ^2}}}dz} = \frac{1}{{{e^\rho } + 1}} = \frac{1}{{\left( { - \rho } \right) + 1}} = \frac{1}{{1 + \Omega }}}$

kwstas12345 · #223

erxmer έγραψε:66)

Ας αποδειχθεί οτι
$\boxed{\displaystyle{\int_{0}^{\infty}{[(x^n+1)^{\frac{1}{n}}-x]dx}=\frac{1}{2n}B(1-2/n, 1/n)}}$

67)
Ας αποδειχθεί οτι
$\boxed{\displaystyle{\frac{1}{\pi}{\int_{0}^{\infty}{ln^4(\frac{x}{x^2+1})\frac{dx}{(x^2+1)^2}}}=\frac{19}{960}{\pi}^4+\frac{1}{2}{\pi}^2ln^22+4ln^42+3\zeta (3)ln2}}$

Για το 67.Έστω $\displaystyle f(a)=\int_{0}^{\infty}{\left(\frac{x}{1+x^2} \right)^a \frac{1}{\left(1+x^2 \right)^2}}dx$ , τότε με τον μετασχηματισμό $\displaystyle x=tany$ έχουμε

$\displaystyle f\left(a \right)=\int_{0}^{\pi/2}{\frac{1}{\cos^2 y}\frac{\left(\tan y \right)^a}{\cos^{-2a-4}y}}dy=\int_{0}^{\pi/2}{\left(\cos y \right)^{a+2}}\sin^{a} y dy=\frac{1}{2}\int_{0}^{1}{(1-x)^{(a+1)/2}x^{(a-1)/2}}dx$ $\displaystyle =\frac{1}{2}\frac{\Gamma \left(\frac{a+3}{2} \right)\Gamma \left(\frac{a+1}{2} \right){}}{\Gamma \left(a+2 \right)}$

Επομένως: $\displaystyle \int_{0}^{\infty}{\left(\ln\left(\frac{x}{1+x^2} \right) \right)^4 \cdot\frac{1}{\left(1+x^2 \right)^2}}dx=\frac{1}{2}\frac{d^{4}}{da^4}\left\{\frac{\Gamma \left(\frac{a+3}{2} \right)\Gamma \left(\frac{a+1}{2} \right){}}{\Gamma \left(a+2 \right)} \right\}_{a=0}$ .

Από αυτό το σημείο και μετα το ζητούμενο είναι θέμα πράξεων, ωστόσο η 4η παράγωγος περιλαμβάνει γνωστές τιμές των συναρτήσεων $\displaystyle \psi ^{(0)}},\psi ^{\left(2 \right)}$ στα σημεία 1/2,3/2,2

.

Οι τιμές αυτές είναι γνωστές αφού για παράδειγμα: $\displaystyle \psi ^{(2)}\left(1/2 \right)=-2\sum_{k=0}^{\infty}{(k+1/2)^{-3}}=-14\zeta(3)$ και $\displaystyle \psi \left(1/2 \right)=-\gamma -\sum_{n=1}^{\infty}{\frac{1}{n\left(2n-1 \right)}}=...=-\gamma -2 \ln 2$ .

Τελικά θα προκύψει ότι: $\displaystyle \int_{0}^{\infty}{\ln^4\left(\frac{x}{1+x^2} \right)\left(1+x^2 \right)^{-2}dx}=\frac{19\pi^5}{960}+\frac{\pi^3}{2}\ln^2 2+4\pi\ln^4 2+3\pi\zeta(3)\ln 2$ .

Προκύπτει επίσης ότι (αν δεν υπάρχει λάθος στις πράξεις): $\displaystyle \int_{0}^{\infty}{\ln^2\left(\frac{x}{1+x^2} \right)}\frac{1}{\left(1+x^2 \right)}dx=\frac{\pi^3}{48}+\frac{\pi\gamma ^2}{2}-\frac{\pi \gamma }{2 }+\pi \ln^2 2$

Το ανάπτυγμα της συνάρτησης

γύρω από το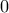

, υπάρχει εδώ: http://www.wolframalpha.com/input/?i=%5 ... 28-1%29%5D

Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Μέλη σε σύνδεση