Γενικευμένα Ολοκληρώματα

#81

Μια ακόμα λύση με μιγαδική για το

Κοτρώνης Αναστάσιος έγραψε: $\displaystyle{35)}$ $\displaystyle{\int_{0}^{+\infty}\frac{\sqrt{x}\ln x}{1+x^2}\,dx}$ .

τη γράφω γιατί είναι διαφέρει από του Σεραφείμ στο ότι δουλεύει απευθείας με την ολοκληρωτέα συνάρτηση.

Θέτω $\displaystyle{f(z)=\frac{z^{1/2}\ln z}{1+z^2}\,dz}$ με $\ln z=\ln|z|+i\theta,\,\,\theta\in[0,2\pi)$ η οποία έχει απλούς πόλους τα $\pm i$ και ολοκληρώνω στο μονοπάτι που αποτελείται από:

$\bullet$ τον κύκλο $C_{1}$ ακτίνας R>1

, κέντρου

με τη θετική φορά,

$\bullet$ τον κύκλο $C_{3}$ ακτίνας r<1

, κέντρου

με τη αρνητική φορά,

$\bullet$ το τμήμα $\displaystyle{C_{2}}$ στον $\displaystyle{xx{'}}$ από το (R,0)

στο

και

$\bullet$ το τμήμα $\displaystyle{C_{4}}$ στον xx{'}

από το

στο

.

Τώρα έχουμε:

$\displaystyle{\Big|\int_{C_{1}}f(z)\,dz\Big|=\Big|\int_{0}^{2\pi}\frac{R^{1/2}e^{i\theta/2}(\ln R+i\theta)Rie^{i\theta}}{1+R^2e^{2i\theta}}\,d\theta\Big|\leq\frac{R^{3/2}}{R^2-1}2\pi\sqrt{\ln^22\pi+4\pi^2}\stackrel{R\to+\infty}{\longrightarrow}0}$ ,

$\displaystyle{\Big|\int_{C_{3}}f(z)\,dz\Big|=\Big|\int_{2\pi}^{0}\frac{r^{1/2}e^{i\theta/2}(\ln r+i\theta)rie^{i\theta}}{1+r^2e^{2i\theta}}\,d\theta\Big|\leq\frac{r^{3/2}}{r^2-1}2\pi\sqrt{\ln^22\pi+4\pi^2}\stackrel{r\to0}{\longrightarrow}0}$ ,

$\displaystyle{\int_{C_{2}}f(z)\,dz=\int_{R}^{r}\frac{(xe^{2\pi i})^{1/2}(\ln x+2\pi i)}{1+(xe^{2\pi i})^2}\,dx=-\int_{R}^{r}\frac{x^{1/2}(\ln x+2\pi i)}{1+x^2}\,dx=}$

$\displaystyle{\int_{r}^{R}\frac{x^{1/2}(\ln x+2\pi i)}{1+x^2}\,dx\stackrel{(r,R)\to(0,+\infty)}{\longrightarrow}\int_{0}^{+\infty}\frac{x^{1/2}\ln x}{1+x^2}\,dx+2\pi i\int_{0}^{+\infty}\frac{x^{1/2}}{1+x^2}\,dx}$ ,

$\displaystyle{\int_{C_{4}}f(z)\,dz=\int_{r}^{R}\frac{(xe^{0i})^{1/2}(\ln x+0i)}{1+(xe^{0i})^2}\,dx=\int_{r}^{R}\frac{x^{1/2}\ln x}{1+x^2}\,dx\stackrel{(r,R)\to(0,+\infty)}{\longrightarrow}\int_{0}^{+\infty}\frac{x^{1/2}\ln x}{1+x^2}\,dx}$ .

Επιπλέον:

$\displaystyle{\mathrm{Res}(z=i,f(z))=\lim_{z\to i}\frac{z^{1/2}\ln z}{z+i}=\frac{(e^{i\pi/2})^{1/2}(\ln|i|+i\pi/2)}{2i}=\frac{\sqrt{2}\pi}{8}+i\frac{\sqrt{2}\pi}{8}}$ ,

$\displaystyle{\mathrm{Res}(z=-i,f(z))=\lim_{z\to -i}\frac{z^{1/2}\ln z}{z-i}=\frac{(e^{i3\pi/2})^{1/2}(\ln|i|+i3\pi/2)}{-2i}=\frac{3\sqrt{2}\pi}{8}-i\frac{3\sqrt{2}\pi}{8}}$ .

Από το θεώρημα των υπολοίπων τώρα θα είναι

$\displaystyle{\sqrt{2}\pi^2 i+\frac{\sqrt{2}\pi^2}{2}=2\pi i\sum\mathrm{Res}=2\int_{0}^{+\infty}\frac{x^{1/2}\ln x}{1+x^2}\,dx+2\pi i\int_{0}^{+\infty}\frac{x^{1/2}}{1+x^2}\,dx}$ ,

από όπου εξισώνοντας τα πραγματικά μέρη παίρνουμε $\displaystyle{\int_{0}^{+\infty}\frac{x^{1/2}\ln x}{1+x^2}\,dx=\frac{\sqrt{2}\pi^2}{4}}$ .

Συμπληρωματικά, εξισώνοντας και φανταστικά μέρη, βγαίνει και ότι $\displaystyle{\int_{0}^{+\infty}\frac{x^{1/2}}{1+x^2}\,dx=\frac{\sqrt{2}\pi}{2}}$ .

#82

Ένα χαριτωμένο:

Αν $a_{1},\ldots,a_{n},b_{1},\ldots,b_{m},b\in\mathbb R$ με $\displaystyle{b>\sum_{i=1}^{n}|a_{i}|+\sum_{j=1}^{m}|b_{j}|}$ , υπολογίστε το $\displaystyle{\int_{0}^{+\infty}\left(\prod_{i=1}^{n}\frac{\sin(a_{i}x)}{x}\right)\left(\prod_{j=1}^{m}\cos(b_{j}x)\right)\frac{\sin(bx)}{x}\,dx}$ .

erxmer · #83

Nα αποδειχθεί οτι $\boxed{\displaystyle{\int_{0}^{+\infty}{\frac{cosx^2-cosx}{x}}dx=\frac{\gamma }{2}}}$

$\gamma = Euler \ constant$

erxmer · #84

$\boxed{\displaystyle{\int_{0}^{+\infty}{\frac{(1+z)^{-n}dz}{log^2z+{\pi}^2}}=(-1)^{n-1}\int_{0}^{1}{\begin{pmatrix} t\\ n \end{pmatrix}dt}}}$

όπου
$\begin{pmatrix} t\\ n \end{pmatrix}=\frac{t(t-1)...(t-n+1)}{n!}, n\geq 1, n \in N^*$

#85

Το

είναι το

εδώ.

#86

Κοτρώνης Αναστάσιος έγραψε: $\displaystyle{17)}$ Σαν συνέχεια των ποστς

viewtopic.php?f=9&t=7314
viewtopic.php?f=9&t=7877&p=46538#p46538 και
viewtopic.php?f=9&t=8239 ,

μια με θεωρητικό αλλά και πρακτικό ενδιαφέρον που αφορά τα ολολκληρώματα Frullani.

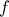Για , ας υπολογισθεί το ολοκλήρωμα $\displaystyle{\int_{0}^{+\infty}\frac{f(ax)-f(bx)}{x}\,dx}$ όπου η $\displaystyle{f}$ είναι συνεχής στο $\displaystyle{[0,+\infty)}$ σε κάθε μια από τις παρακάτω περιπτώσεις:

$\displaystyle{i)}$ Το ολοκλήρωμα $\displaystyle{\int_{1}^{+\infty}\frac{f(t)}{t}\,dt}$ συγκλίνει,

$\displaystyle{ii)}$ $\displaystyle{f(x+T)=f(x)}$ για κάποιο $\displaystyle{T>0}$ και για κάθε $\displaystyle{x\geq0}$ ,

$\displaystyle{iii)}$ $\displaystyle{\lim_{x\to+\infty}f(x)=\ell\in\mathbb{R}}$ .

Δίνω μια λύση γιατί ξεχάστηκε:

Έχουμε $\displaystyle{\int_{h}^{+\infty}\frac{f(ax)-f(bx)}{x}\,dx\stackrel{\boxed{*}}{=}\int_{h}^{+\infty}\frac{f(ax)}{x}\,dx-\int_{h}^{+\infty}\frac{f(bx)}{x}\,dx\stackrel{ax=y,\,bx=y}{=}}$

$\displaystyle{\int_{ah}^{+\infty}\frac{f(y)}{y}\,dy-\int_{bh}^{+\infty}\frac{f(y)}{y}\,dy=-\int_{bh}^{ah}\frac{f(y)}{y}\,dy\stackrel{\ln y=t}{=}-\int_{\ln bh}^{\ln ah}f(e^t)\,dt=\left(\ln (b/a)\right)f(e^{\xi})}$ για κάποιο $\xi\in(\ln bh,\ln ah)$ .

Όμως $h\to 0\Rightarrow \ln ah\to-\infty\Rightarrow f(e^{\xi})\to f(0)$ λόγω συνέχειας της

στο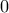

, συνεπώς $\displaystyle{\int_{0}^{+\infty}\frac{f(ax)-f(bx)}{x}\,dx=f(0)\ln(b/a)}$ .

$\boxed{*}$ Επειδή το $\displaystyle{\int_{1}^{+\infty}\frac{f(x)}{x}\,dx}$ συγκλίνει.

ii)

$\bullet$ Αν $\displaystyle{\int_{0}^{T}f(x)\,dx=0}$ .

Τότε για κάθε $\displaystyle{M>0}$ , είναι $\displaystyle{\Big|\int_{1}^{M}f(x)\,dx\Big|\leq\Big|\sum_{k=1}^{[(M-1)/T]}\int_{1+(k-1)T}^{1+kT}f(x)\,dx\Big|+\Big|\int_{1+[(M-1)/T]T}^{M}f(x)\,dx\Big|\leq0+T\cdot\max_{x\in[0,T]}|f(x)|}$ και επειδή $1/x\searrow0$ , από το κριτήριο του Dirichlet, το $\displaystyle{\int_{1}^{+\infty}\frac{f(x)}{x}\,dx}$ συγκλίνει, οπότε από το

το ολοκλήρωμα ισούται με $f(0)\ln(b/a)$ .

$\bullet$ Αν $\displaystyle{\int_{0}^{T}f(x)\,dx\neq0}$ , τότε $\displaystyle{\int_{h}^{+\infty}\frac{f(ax)-f(bx)}{x}\,dx=\int_{h}^{+\infty}\frac{g(ax)-g(bx)}{x}\,dx}$ , όπου $g(x)=f(x)-\frac{1}{T}\int_{0}^{T}f(x)\,dx$ , με $\int_{0}^{T}g(x)\,dx=0$ ,

οπότε πάλι από την προηγούμενη περίπτωση και την αναγωγή στο ii)

έχουμε $\displaystyle{\int_{0}^{+\infty}\frac{f(ax)-f(bx)}{x}\,dx=g(0)\ln(b/a)=}$ $\left(f(0)-(1/T)\int_{0}^{T}f(x)\,dx\right)\ln(b/a)$ .

iii)

Είναι $\displaystyle{\int_{0}^{+\infty}\frac{f(ax)-f(bx)}{x}\,dx=\lim_{M\to+\infty}\lim_{h\to0}\int_{h}^{M}\frac{f(ax)-f(bx)}{x}\,dx}$ . Θέτω $\displaystyle{(1/x)\int_{0}^{x}f(t)\,dt}$ και έχουμε:

$\displaystyle{\int_{h}^{M}\frac{f(ax)-f(bx)}{x}\,dx=\int_{h}^{M}\frac{f(ax)}{x}\,dx-\int_{h}^{M}\frac{f(bx)}{x}\,dx\stackrel{ax=y,\,bx=y}{=}\int_{ah}^{aM}\frac{f(x)}{x}\,dx-\int_{bh}^{bM}\frac{f(x)}{x}\,dx=\int_{ah}^{bh}\frac{f(x)}{x}\,dx-\int_{aM}^{bM}\frac{f(x)}{x}\,dx=}$

$\displaystyle{\int_{ah}^{bh}\frac{(xF(x)){'}}{x}\,dx-\int_{aM}^{bM}\frac{(xF(x)){'}}{x}\,dx=F(bh)-F(ah)+\int_{ah}^{bh}\frac{F(x)}{x}\,dx-F(bM)+F(aM)-\int_{aM}^{bM}\frac{F(x)}{x}\,dx\stackrel{\ln x=y}{=}}$

$\displaystyle{F(bh)-F(ah)+\int_{\ln ah}^{\ln bh}F(e^{y})\,dy-F(bM)+F(aM)-\int_{\ln aM}^{\ln bM}F(e^{y})\,dy=}$

$\displaystyle{F(bh)-F(ah)-F(bM)+F(aM)+\ln(b/a)\left(F(e^{\xi_{1}})-F(e^{\xi_{2}})\right)\qquad\boxed{1}}$

για κάποια $\xi_{1}\in(\ln ah,\ln bh)$ και $\xi_{2}\in(\ln aM,\ln bM)$ .

Επειδή τώρα $F(ah),F(bh)\stackrel{h\to0}{\longrightarrow}f(0)$ ,

$F(aM),F(bM)\stackrel{M\to+\infty}{\longrightarrow}\ell$ ,

$h\to0\Rightarrow\xi_{1}\to-\infty$ και

$M\to+\infty\Rightarrow\xi_{2}\to+\infty$ , παίρνοντας στην $\boxed{1}$ , πρώτα όριο ως προς $h\to0$ και έπειτα ως προς $M\to+\infty$ , έχουμε ότι $\displaystyle{\int_{0}^{+\infty}\frac{f(ax)-f(bx)}{x}\,dx=\left(f(0)-\ell\right)\ln(b/a)}$ .

#87

erxmer έγραψε: $\boxed{\displaystyle{\int_{0}^{+\infty}{\frac{(1+z)^{-n}dz}{log^2z+{\pi}^2}}=(-1)^{n-1}\int_{0}^{1}{\begin{pmatrix} t\\ n \end{pmatrix}dt}}}$

όπου
$\begin{pmatrix} t\\ n \end{pmatrix}=\frac{t(t-1)...(t-n+1)}{n!}, n\geq 1, n \in N^*$

Είναι το πρόβλημα 3276

του Monthly το οποίο υπάρχει στον τόμο του 1928 σελ. 495-500. Μαζί με μια γενίκευση που δίνει ο λύτης είναι τρισήμιση σελίδες.

erxmer · #88

Nα υπολογιστούν τα ακόλουθα:

39) $\boxed{\displaystyle{\int_{-\infty}^{+\infty}{\frac{xsinx}{x^2+4x+20}dx}}}$

40) $\boxed{\displaystyle{\int_{0}^{+\infty}{\frac{4cos(\lambda x)}{e^x+e^{-x}}dx}, \lambda \in R}}$

41) $\boxed{\displaystyle{\int_{-\infty}^{+\infty}{\frac{e^{-ix}}{x^2-2x+4}dx}}}$

erxmer · #89

Nα αποδειχθούν τα ακόλουθα:

42) $\boxed{\displaystyle{\int_{0}^{\infty}{\frac{xdx}{(x^2+1)(x^4+x^2+1)}}=\frac{1}{2}\frac{\pi}{3\sqrt{3}}}}$

43) $\boxed{\displaystyle{\int_{0}^{\infty}{\frac{dx}{(x^4+(1+\sqrt{2})x^2+1)(x^{100}-x^{98}+...+1)}=\frac{\pi}{2(1+\sqrt{2})}}}}$

44) $\boxed{\displaystyle{\int_{0}^{\infty}{x^{2n}e^{-px^2}dx=\frac{(2n)!}{2^{2n+1}n!p^{n+1/2}}\sqrt{\pi}}}} n \in N, p>0$

#90

erxmer έγραψε:44) $\boxed{\displaystyle{\int_{0}^{\infty}{x^{2n}e^{-px^2}dx=\frac{(2n)!}{2^{2n+1}n!p^{n+1/2}}\sqrt{\pi}}}} n \in N, p>0$

$\displaystyle{\int\limits_0^\infty {{x^{2n}}{e^{ - p{x^2}}}dx} = \mathop = \limits^{x = \sqrt y } = \frac{1}{2}\int\limits_0^\infty {{y^{n - 1/2}}{e^{ - py}}dy} = \mathop = \limits^{\left\lfloor * \right\rfloor } = \frac{1}{2} \cdot \frac{{\Gamma \left( {n + 1/2} \right)}}{{{p^{n + 1/2}}}} = \frac{{\Gamma \left( n \right)\Gamma \left( {n + 1/2} \right)}}{{2\Gamma \left( n \right){p^{n + 1/2}}}} = \mathop = \limits^{\left\lfloor {**} \right\rfloor } = \frac{{{2^{1 - 2n}}\sqrt \pi \Gamma \left( {2n} \right)}}{{2\left( {n - 1} \right)!{p^{n + 1/2}}}} = }$

$\displaystyle{ = \frac{{\left( {2n - 1} \right)!\sqrt \pi }}{{{2^{2n}}\left( {n - 1} \right)!{p^{n + 1/2}}}} = \frac{{\left( {2n - 1} \right)!\sqrt \pi 2n}}{{{2^{2n}}2n\left( {n - 1} \right)!{p^{n + 1/2}}}} = \frac{{\left( {2n} \right)!\sqrt \pi }}{{{2^{2n + 1}}n!{p^{n + 1/2}}}}}$

$\displaystyle{\left\lfloor * \right\rfloor :\int\limits_0^\infty {{x^a}{e^{ - px}}dx} = \frac{{\Gamma \left( {a + 1} \right)}}{{{p^{a + 1}}}}}$ http://mathworld.wolfram.com/LaplaceTransform.html

$\displaystyle{\left\lfloor {**} \right\rfloor :\Gamma \left( z \right)\Gamma \left( {z + 1/2} \right) = {2^{1 - 2n}}\sqrt \pi \Gamma \left( {2z} \right)}$ http://en.wikipedia.org/wiki/Gamma_function

#91

erxmer έγραψε:39) $\boxed{\displaystyle{\int_{-\infty}^{+\infty}{\frac{xsinx}{x^2+4x+20}dx}}}$

Έστω η μιγαδική συνάρτηση $\displaystyle{f\left( z \right) = \frac{{z{e^{iz}}}}{{{z^2} + 4z + 20}}}$ που είναι μερόμορφη στο άνω ημιεπίπεδο με απλό πόλο (στο άνω ημιεπίπεδο) τον $\displaystyle{u = - 2 + 4i}$

και residue $\displaystyle{Res\left( {f\left( z \right);z = - 2 + 4i} \right) = \mathop {\lim }\limits_{z \to - 2 + 4i} \left( {\frac{{z{e^{iz}}\left( {z + 2 - 4i} \right)}}{{{z^2} + 4z + 20}}} \right) = .. = \frac{{\left( { - 2 + 4i} \right){e^{ - 2i}}}}{{8{e^4}i}}}$

Θεωρούμε το άνω ημικύκλιο $\displaystyle{\left( C \right)}$ με διάμετρο $\displaystyle{AB:A\left( { - R,0} \right){\text{ \& }}B\left( {R,0} \right)}$ . Επί του τόξου έχουμε $\displaystyle{z = {\text{R}}{e^{i\theta }}}$ με $\displaystyle{\theta \in \left[ {0,\pi } \right]}$

Οπότε $\displaystyle{\left| {f\left( z \right)} \right| = \left| {\frac{z}{{{z^2} + 4z + 20}}} \right| \cdot \left| {{e^{iR\left( {\cos \left( \theta \right) + i\sin \left( \theta \right)} \right)}}} \right| \leqslant \frac{{R{e^{ - R\sin \left( \theta \right)}}}}{{{R^2} - 4R - 20}}\xrightarrow{{R \to \infty }}0 \Rightarrow \mathop {\lim }\limits_{R \to \infty } \left| {f\left( z \right)} \right| = 0}$

Επομένως $\displaystyle{\int\limits_C {f\left( z \right)dz} = \int\limits_{ - \infty }^{ + \infty } {\frac{{x{e^{ix}}}}{{{x^2} + 4x + 20}}dx} }$ . Όμως $\displaystyle{\frac{1}{{2\pi i}}\int\limits_C {f\left( z \right)dz} = Res\left( {f\left( z \right);z = - 2 + 4i} \right) = \frac{{\left( { - 2 + 4i} \right){e^{ - 2i}}}}{{8{e^4}i}}}$ ,

άρα $\displaystyle{\int\limits_{ - \infty }^{ + \infty } {\frac{{x{e^{ix}}}}{{{x^2} + 4x + 20}}dx} = 2\pi i\frac{{\left( { - 2 + 4i} \right){e^{ - 2i}}}}{{8{e^4}i}} = \pi \frac{{\left( { - 1 + 2i} \right)\left( {\cos \left( 2 \right) - i\sin \left( 2 \right)} \right)}}{{2 \cdot {e^4}}}}$

και τελικά $\displaystyle{\int\limits_{ - \infty }^{ + \infty } {\frac{{x\left( {\cos \left( x \right) + i\sin \left( x \right)} \right)}}{{{x^2} + 4x + 20}}dx} = \pi \frac{{ - \cos \left( 2 \right) + 2\sin \left( 2 \right) + i\left( {\sin \left( 2 \right) + 2\cos \left( 2 \right)} \right)}}{{2 \cdot {e^4}}}}$

Εξισώνοντας πραγματικά και φανταστικά μέρη προκύπτει $\displaystyle{\int\limits_{ - \infty }^{ + \infty } {\frac{{x\sin \left( x \right)}}{{{x^2} + 4x + 20}}dx} = \frac{{\left( {\sin \left( 2 \right) + 2\cos \left( 2 \right)} \right)\pi }}{{2 \cdot {e^4}}}}$

#92

erxmer έγραψε:40) $\boxed{\displaystyle{\int_{0}^{+\infty}{\frac{4cos(\lambda x)}{e^x+e^{-x}}dx}, \lambda \in R}}$

Θεωρούμε την μιγαδική συνάρτηση $\displaystyle{f\left( z \right) = \frac{{{e^{i\lambda z}}}}{{{e^z} + {e^{ - z}}}}}$ που είναι αναλυτική στο ορθογώνιο $\displaystyle{\left( c \right):ABCD}$ , όπου $\displaystyle{A\left( {M,0} \right){\text{ }}{\text{, }}B\left( {M,i\pi } \right){\text{ }}{\text{, }}C\left( { - M,i\pi } \right){\text{ \& }}D\left( { - M,0} \right)}$

: erxm.jpg (18.46 KiB) Προβλήθηκε 2600 φορές

με μοναδικό απλό πόλο τον $\displaystyle{i\pi /2}$ , όπου έχουμε ολοκληρωτικό υπόλοιπο $\displaystyle{Res\left( {f\left( z \right);z = i\frac{\pi }{2}} \right) = \mathop {\lim }\limits_{z \to i\frac{\pi }{2}} \left( {\frac{{{e^{i\lambda z}}}}{{{e^z} + {e^{ - z}}}}\left( {z - i\frac{\pi }{2}} \right)} \right) = \frac{{{e^{ - \lambda \pi /2}}}}{{2i}}}$
Τότε $\displaystyle{\int\limits_c {f\left( z \right)dz} = 2\pi i \cdot Res\left( {f\left( z \right);z = i\frac{\pi }{2}} \right) = \pi \cdot {e^{ - \lambda \pi /2}}}$

Επί της πλευράς

έχουμε $\displaystyle{\left| {f\left( z \right)} \right| = \left| {\frac{{{e^{i\lambda \left( {{\rm M} + iy} \right)}}}}{{{e^{{\rm M} + iy}} + {e^{ - \left( {{\rm M} + iy} \right)}}}}} \right| \leqslant \frac{{{e^{ - \lambda y}}}}{{{e^{\rm M}} - {e^{ - M}}}}\xrightarrow{{M \to \infty }}0}$ , όμοια και επί της

, επομένως για $\displaystyle{M \to + \infty }$ προκύπτει

$\displaystyle{\int\limits_c {f\left( z \right)dz} = \int\limits_{ - \infty }^{ + \infty } {\frac{{{e^{i\lambda x}}}}{{{e^x} + {e^{ - x}}}}dx} + \int\limits_{ + \infty }^{ - \infty } {\frac{{{e^{i\lambda \left( {x + i\pi } \right)}}}}{{{e^{x + i\pi }} + {e^{ - \left( {x + i\pi } \right)}}}}dx} = \int\limits_{ - \infty }^{ + \infty } {\frac{{{e^{i\lambda x}}}}{{{e^x} + {e^{ - x}}}}dx} - {e^{ - \lambda \pi }}\int\limits_{ + \infty }^{ - \infty } {\frac{{{e^{i\lambda x}}}}{{{e^x} + {e^{ - x}}}}dx} = }$

$\displaystyle{ = \left( {1 + {e^{ - \lambda \pi }}} \right)\int\limits_{ - \infty }^{ + \infty } {\frac{{\cos \left( {\lambda x} \right) + i\sin \left( {\lambda x} \right)}}{{{e^x} + {e^{ - x}}}}dx} = \left( {1 + {e^{ - \lambda \pi }}} \right)\int\limits_{ - \infty }^{ + \infty } {\frac{{\cos \left( {\lambda x} \right)}}{{{e^x} + {e^{ - x}}}}dx} = 2\left( {1 + {e^{ - \lambda \pi }}} \right)\int\limits_0^{ + \infty } {\frac{{\cos \left( {\lambda x} \right)}}{{{e^x} + {e^{ - x}}}}dx} }$

Τελικά $\displaystyle{\int\limits_0^{ + \infty } {\frac{{4\cos \left( {\lambda x} \right)}}{{{e^x} + {e^{ - x}}}}dx} = \frac{2}{{1 + {e^{ - \lambda \pi }}}}\int\limits_c {f\left( z \right)dz} = \frac{2}{{1 + {e^{ - \lambda \pi }}}}\int\limits_c {f\left( z \right)dz} = \frac{{2\pi \cdot {e^{ - \lambda \pi /2}}}}{{1 + {e^{ - \lambda \pi }}}} = \frac{{2\pi }}{{{e^{\lambda \pi /2}} + {e^{ - \lambda \pi /2}}}}}$ .

#93

erxmer έγραψε:41) $\boxed{\displaystyle{\int_{-\infty}^{+\infty}{\frac{e^{-ix}}{x^2-2x+4}dx}}}$

Έστω η μιγαδική συνάρτηση $\displaystyle{f\left( z \right) = \frac{{{e^{ - iz}}}}{{{z^2} - 2z + 4}}}$ που είναι αναλυτική στο κάτω ημιεπίπεδο με απλό πόλο τον $\displaystyle{u = 1 - i\sqrt 3 }$ και ολοκληρωτικό υπόλοιπο

$\displaystyle{Res\left( {f\left( z \right);z = 1 - i\sqrt 3 } \right) = \mathop {\lim }\limits_{z \to 1 - i\sqrt 3 } \left( {\frac{{{e^{ - iz}}\left( {z - 1 + i\sqrt 3 } \right)}}{{{z^2} - 2z + 4}}} \right) = \frac{{{e^{ - \sqrt 3 - i}}}}{{ - 2i\sqrt 3 }}}$

: erxm2.jpg (18.96 KiB) Προβλήθηκε 2592 φορές

Θεωρούμε το κάτω ημικύκλιο $\displaystyle{\left( C \right)}$ με διάμετρο $\displaystyle{AB:A\left( {R,0} \right){\text{ \& }}B\left( { - R,0} \right)}$ . Επί του τόξου έχουμε $\displaystyle{z = {\text{R}}{e^{i\theta }}}$ με $\displaystyle{\theta \in \left[ {\pi ,2\pi } \right]}$ .

Οπότε $\displaystyle{\left| {f\left( z \right)} \right| = \left| {\frac{{{e^{ - iM\left( {\cos \left( \theta \right) + i\sin \left( \theta \right)} \right)}}}}{{{z^2} - 2z + 4}}} \right| \leqslant \frac{{{e^{M\sin \left( \theta \right)}}}}{{{M^2} - 2M - 4}}\xrightarrow[{\theta \in \left[ {\pi ,2\pi } \right]}]{{M \to \infty }}0 \Rightarrow \mathop {\lim }\limits_{M \to \infty } \left| {f\left( z \right)} \right| = 0}$

Επομένως $\displaystyle{\int\limits_C {f\left( z \right)dz} = \int\limits_{ + \infty }^{ - \infty } {\frac{{{e^{ - ix}}}}{{{x^2} - 2x + 4}}dx} \Rightarrow \int\limits_{ - \infty }^{ + \infty } {\frac{{{e^{ - ix}}}}{{{x^2} - 2x + 4}}dx} = - \int\limits_C {f\left( z \right)dz} }$

Όμως $\displaystyle{\frac{1}{{2\pi i}}\int\limits_C {f\left( z \right)dz} = Res\left( {f\left( z \right);z = 1 - i\sqrt 3 } \right) = \frac{{{e^{ - \sqrt 3 - i}}}}{{ - 2i\sqrt 3 }}}$

Τελικά $\displaystyle{\int\limits_{ - \infty }^{ + \infty } {\frac{{{e^{ - ix}}}}{{{x^2} - 2x + 4}}dx} = - 2\pi i\frac{{{e^{ - \sqrt 3 - i}}}}{{ - 2i\sqrt 3 }} = \frac{{\pi {e^{ - \sqrt 3 }}\left( {\cos \left( 1 \right) - i\sin \left( 1 \right)} \right)}}{{\sqrt 3 }}}$ .

erxmer · #94

Nα υπολογιστούν τα ακόλουθα:

45) $\boxed{\displaystyle{\int_{-\infty}^{+\infty}{(1+\frac{x^2}{n-1})^{-n/2}}}}$

46) $\boxed{\displaystyle{\int_{0}^{\pi/2}{x^2ln^2(2cosx)}dx=\frac{11*\pi*\zeta (4)}{16}}}$

47) $\boxed{\displaystyle{\int_{0}^{+\infty}{(\frac{x^2}{x^4+30x^2+1})^6}dx}}$

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

#95

erxmer έγραψε:45) $\boxed{\displaystyle{\int_{-\infty}^{+\infty}{(1+\frac{x^2}{n-1})^{-n/2}}}}$

$\displaystyle{\int\limits_{ - \infty }^{ + \infty } {{{\left( {1 + \frac{{{x^2}}}{{n - 1}}} \right)}^{ - n/2}}dx} = \mathop = \limits^{x = y\sqrt {n - 1} } = \sqrt {n - 1} \int\limits_{ - \infty }^{ + \infty } {\frac{1}{{{{\left( {1 + {y^2}} \right)}^{n/2}}}}dy} = \mathop = \limits^{even} = 2\sqrt {n - 1} \int\limits_0^\infty {\frac{1}{{{{\left( {1 + {y^2}} \right)}^{n/2}}}}dy} = \mathop = \limits^{y = \sqrt x } = }$

$\displaystyle{ = \sqrt {n - 1} \int\limits_0^\infty {\frac{1}{{\sqrt x {{\left( {1 + x} \right)}^{n/2}}}}dx} = \frac{{\sqrt {n - 1} }}{{\Gamma \left( {n/2} \right)}}\int\limits_0^\infty {\frac{1}{{\sqrt x }}\frac{{\Gamma \left( {n/2} \right)}}{{{{\left( {1 + x} \right)}^{n/2}}}}dx} = \frac{{\sqrt {n - 1} }}{{\Gamma \left( {n/2} \right)}}\int\limits_0^\infty {\frac{1}{{\sqrt x }}\left( {\int\limits_0^\infty {{y^{\dfrac{n}{2} - 1}}{e^{ - \left( {x + 1} \right)y}}dy} } \right)dx} = }$

$\displaystyle{ = \frac{{\sqrt {n - 1} }}{{\Gamma \left( {n/2} \right)}}\int\limits_0^\infty {{y^{\dfrac{n}{2} - 1}}{e^{ - y}}\left( {\int\limits_0^\infty {\frac{1}{{\sqrt x }}{e^{ - xy}}dx} } \right)dy} = \frac{{\sqrt {n - 1} }}{{\Gamma \left( {n/2} \right)}}\int\limits_0^\infty {{y^{\dfrac{n}{2} - 1}}{e^{ - y}}\frac{{\sqrt \pi }}{{\sqrt y }}dy} = \frac{{\sqrt \pi \sqrt {n - 1} }}{{\Gamma \left( {n/2} \right)}}\int\limits_0^\infty {{y^{\dfrac{{n - 3}}{2}}}{e^{ - y}}dy} = \boxed{\frac{{\sqrt \pi \sqrt {n - 1} }}{{\Gamma \left( {\dfrac{n}{2}} \right)}}\Gamma \left( {\frac{{n - 1}}{2}} \right)}}$

Γνωστές σχέσεις 1) $\displaystyle{\Gamma \left( z \right) = \int\limits_0^\infty {{x^{z - 1}}{e^{ - x}}dx} }$ , 2) $\displaystyle{\int\limits_0^\infty {{x^z}{e^{ - ax}}dx} = \frac{{\Gamma \left( {z + 1} \right)}}{{{a^{z + 1}}}}}$

Αν $\displaystyle{n \in {N^*}}$ χωράει και περαιτέρω επεξεργασία με διάκριση άρτιου - περιττού.

erxmer · #96

Nα υπολογιστούν τα ακόλουθα:

48) $\boxed{\displaystyle {\int_{0}^{\infty}{\frac{dx}{(x^4+2ax^2+1)^2}=\frac{(2a+3)\pi}{2^{7/2}(a+1)^{3/2}}}}}$

49) $\boxed{\displaystyle {\int_{0}^{\infty}{\frac{x^{29}dx}{(5x^2+49)^{17}}=\frac{14!}{2(16)!5^{15}49^2}}}}$

50) $\boxed{\displaystyle{\int_{0}^{\infty}{\frac{3x^3dx}{(x^4+4x^2+1)^5}=\frac{5(60+7\sqrt{3}ln(7-4\sqrt{3}))}{20736}}}}$

#97

erxmer έγραψε:49) $\boxed{\displaystyle {\int_{0}^{\infty}{\frac{x^{29}dx}{(5x^2+49)^{17}}=\frac{14!}{2(16)!5^{15}49}}}}$

Λοιπόν .. $\displaystyle{I = \int\limits_0^\infty {\frac{{{x^{29}}}}{{{{\left( {5{x^2} + 49} \right)}^{17}}}}dx} = \int\limits_0^\infty {\frac{{{{\left( {{x^2}} \right)}^{14}}x}}{{{{\left( {5{x^2} + 49} \right)}^{17}}}}dx} = \mathop = \limits^{{x^2} = y} = \frac{1}{2}\int\limits_0^\infty {\frac{{{y^{14}}}}{{{{\left( {5y + 49} \right)}^{17}}}}dy} = \mathop = \limits^{\big{y = \dfrac{{49}}{5}x}} = }$

$\displaystyle{ = \frac{1}{{2 \cdot {{49}^2} \cdot {5^{15}}}}\int\limits_0^\infty {\frac{{{x^{14}}}}{{{{\left( {x + 1} \right)}^{17}}}}dx} = \frac{1}{{2 \cdot {{49}^2} \cdot {5^{15}}}}\int\limits_0^\infty {{{\left( {\frac{x}{{x + 1}}} \right)}^{14}}\frac{1}{{{{\left( {x + 1} \right)}^3}}}dx} = \mathop {\mathop = \limits_{\big{dx = \dfrac{1}{{{{\left( {1 - y} \right)}^2}}}dy}} }\limits^{\dfrac{x}{{x + 1}} \big{ = y}} = }$

$\displaystyle{ = \frac{1}{{2 \cdot {{49}^2} \cdot {5^{15}}}}\int\limits_0^1 {{y^{14}}\left( {1 - y} \right)dy} = \frac{1}{{2 \cdot {{49}^2} \cdot {5^{15}}}}\left( {\int\limits_0^1 {{y^{14}}dy} - \int\limits_0^1 {{y^{15}}dy} } \right) = \frac{1}{{2 \cdot {{49}^2} \cdot {5^{15}}}}\left( {\frac{1}{{15}} - \frac{1}{{16}}} \right) = }$

$\displaystyle{ = \frac{1}{{2 \cdot {{49}^2} \cdot {5^{15}} \cdot 15 \cdot 16}} \Rightarrow \boxed{I = \frac{{14!}}{{2 \cdot {{49}^2} \cdot {5^{15}} \cdot 16!}}}}$

#98

erxmer έγραψε:Nα αποδειχθούν τα ακόλουθα:

42) $\boxed{\displaystyle{\int_{0}^{\infty}{\frac{xdx}{(x^2+1)(x^4+x^2+1)}}=\frac{1}{2}\frac{\pi}{3\sqrt{3}}}}$

$\displaystyle{\int\limits_0^\infty {\frac{x}{{\left( {{x^2} + 1} \right)\left( {{x^4} + {x^2} + 1} \right)}}dx} = \mathop = \limits^{x = \sqrt y } = \frac{1}{2}\int\limits_0^\infty {\frac{1}{{\left( {y + 1} \right)\left( {{y^2} + y + 1} \right)}}dy} = \frac{1}{2}\int\limits_0^\infty {\left( {\frac{1}{{y + 1}} - \frac{{y + 1/2}}{{{y^2} + y + 1}} + \frac{1}{2} \cdot \frac{1}{{{y^2} + y + 1}}} \right)dy} = }$

$\displaystyle{ = \frac{1}{2}\left( {\left[ {\ln \left( {\frac{{y + 1}}{{\sqrt {{y^2} + y + 1} }}} \right)} \right]_0^\infty } \right) + \frac{1}{4}\int\limits_0^\infty {\frac{1}{{{y^2} + y + 1}}dy} = \frac{1}{4}\int\limits_0^\infty {\frac{1}{{{{\left( {y + \frac{1}{2}} \right)}^2} + \frac{3}{4}}}dy} = \frac{1}{4}\int\limits_{1/2}^\infty {\frac{1}{{{x^2} + \frac{3}{4}}}dx} = \mathop = \limits^{x = \frac{{\sqrt 3 }}{2}y} = }$

$\displaystyle{ = \frac{1}{{2\sqrt 3 }}\int\limits_{1/\sqrt 3 }^\infty {\frac{1}{{{y^2} + 1}}dy} = \frac{1}{{2\sqrt 3 }}\left[ {\arctan \left( y \right)} \right]_{1/\sqrt 3 }^\infty = \frac{1}{{2\sqrt 3 }}\left( {\frac{\pi }{2} - \frac{\pi }{6}} \right) = \frac{\pi }{{6\sqrt 3 }}}$

mathxl · #99

Μία αόμη λύση για το 42

$\displaystyle{\int\limits_0^\infty {\frac{{xdx}}{{({x^2} + 1)({x^4} + {x^2} + 1)}}} = \int\limits_0^1 {\frac{{xdx}}{{({x^2} + 1)({x^4} + {x^2} + 1)}}} + \int\limits_1^\infty {\frac{{xdx}}{{({x^2} + 1)({x^4} + {x^2} + 1)}}} \mathop = \limits_{dx = - \frac{{du}}{{{u^2}}}}^{x = \frac{1}{u}} }$

$\displaystyle{ = \int\limits_0^1 {\frac{{xdx}}{{({x^2} + 1)({x^4} + {x^2} + 1)}}} + \int\limits_0^1 {\frac{{\frac{1}{u}}}{{(\frac{1}{{{u^2}}} + 1)(\frac{1}{{{u^4}}} + \frac{1}{{{u^2}}} + 1)}}} \frac{{du}}{{{u^2}}} = }$

$\displaystyle{ = \int\limits_0^1 {\frac{{xdx}}{{({x^2} + 1)({x^4} + {x^2} + 1)}}} + \int\limits_0^1 {\frac{{{x^3}dx}}{{({x^2} + 1)({x^4} + {x^2} + 1)}}} = }$

$\displaystyle{ = \int\limits_0^1 {\frac{{x\left( {{x^2} + 1} \right)dx}}{{({x^2} + 1)({x^4} + {x^2} + 1)}}} = \int\limits_0^1 {\frac{{xdx}}{{{x^4} + {x^2} + 1}}} = }$

$\displaystyle{ = \int\limits_0^1 {\frac{{xdx}}{{\left( {{x^2} + x + 1} \right)\left( {{x^2} - x + 1} \right)}}} = - \frac{1}{2}\int\limits_0^1 {\frac{{dx}}{{{x^2} + x + 1}}} + \frac{1}{2}\int\limits_0^1 {\frac{{dx}}{{{x^2} - x + 1}}} = }$

$\displaystyle{ = - \frac{1}{2}\int\limits_0^1 {\frac{{dx}}{{{{\left( {x + \frac{1}{2}} \right)}^2} + \frac{3}{4}}}} + \frac{1}{2}\int\limits_0^1 {\frac{{dx}}{{{{\left( {x - \frac{1}{2}} \right)}^2} + \frac{3}{4}}}} = }$

$\displaystyle{ = - \frac{1}{{\sqrt 3 }}\int\limits_{\frac{{\sqrt 3 }}{3}}^{\sqrt 3 } {\frac{{du}}{{{u^2} + 1}}} + \frac{1}{{\sqrt 3 }}\int\limits_{ - \frac{{\sqrt 3 }}{3}}^{\frac{{\sqrt 3 }}{3}} {\frac{{du}}{{{u^2} + 1}}} = \frac{1}{{\sqrt 3 }}\left( {\left[ {\arctan u} \right]_{ - \frac{{\sqrt 3 }}{3}}^{\frac{{\sqrt 3 }}{3}} - \left[ {\arctan u} \right]_{\frac{{\sqrt 3 }}{3}}^{\sqrt 3 }} \right) = }$

$\displaystyle{ = \frac{1}{{\sqrt 3 }}\left( {\frac{\pi }{6} + \frac{\pi }{6} - \frac{\pi }{3} + \frac{\pi }{6}} \right) = \frac{\pi }{{6\sqrt 3 }}}$

#100

Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Re: Γενικευμένα Ολοκληρώματα

Μέλη σε σύνδεση